Test Matematika: Mana yang lebih luas? A atau B?
Ingat rumus luas 1/2 x alas x tinggi. Temukan rumus segitiga siku-siku dibawah ini!
Segitiga siku-siku mematuhi teorema Pythagoras: jumlah kuadrat dari panjang kedua kaki sama dengan kuadrat panjang hipotenusa: a² + b² = c², di mana a dan b adalah panjang masing – masing kaki dan c adalah panjang hipotenusa. Demikian pula sebaliknya, jika panjang masing – masing kaki memenuhi persamaan tersebut, maka segitiga tersebut pasti memiliki sudut siku-siku di seberang sisi terpanjangnya.
Gunakan angka-angka ini dalam formula luas 1/2 x alas x tinggi
SEGITIGA “A”
Area = 1/2 × alas × tinggi
1/2 x 6 x 6 = 18
Segitiga “A” memiliki 18 m²
SEGITIGA “B”
Area = 1/2 × alas × tinggi
1/2 x 5 x 8 = 20
Segitiga “B” memiliki 20 m²
Beberapa fakta mengenai segitiga siku-siku
- Jumlah sudut-sudut yang bukan siku-siku pasti 90°.
- Jika kaki-kaki segitiga siku-siku sama panjang, maka sudut yang berseberangan dengan kaki-kaki tersebut akan sama besarnya. Dengan demikian karena sifat pertama di atas, maka sudutnya pasti 45°. Dengan teorema Pythagoras, panjang hipotenusa adalah panjang kaki dikali √2.
- Di segitiga siku-siku jika besar sudut lainnya 30° dan 60°, maka panjang hipotenusa dua kali panjang kaki terpendek dan panjang kaki yang lebih panjang sama dengan panjang kaki yang lebih pendek dikali √3

Rumus-rumus segitiga siku-siku
1. Rumus luas segitiga siku-siku
L = ½ x alas x tinggi
L = ½ x a x t
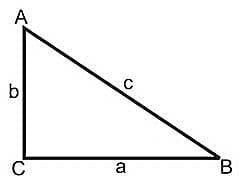
2. Rumus tinggi segitiga siku-siku
Untuk mencari tinggi segitiga siku-siku, berlaku rumus teorema phytagoras.
Apabila panjang sisi a dan panjang sisi b sudah diketahui ukurannya maka panjang sisi c dapat ditentukan dengan persamaan c²= a² + b²
Apabila panjang sisi a dan panjang sisi c sudah diketahui ukurannya maka panjang sisi b dapat ditentukan dengan persamaan b² = c² – a²
Apabila panjang sisi b dan panjang sisi c sudah diketahui ukurannya maka panjang sisi a dapat ditentukan dengan persamaan a² = c² – b²
3. Rumus keliling segitiga siku-siku
K = sisi a + sisi b + sisi c, atau
K = sisi + sisi + sisi
Soal dan jawaban segitiga siku-siku
1. Berapa keliling segitiga jika panjang sisi-sisinya 5 cm, 3 cm dan 4 cm?
Diketahui :
Misalkan
Sisi a = 5 cm
Sisi b = 4 cm
Sisi c = 3 cm
Ditanya :
K . . . . ?
Jawab :
K = sisi a + sisi b + sisi c
K = 5 cm + 4 cm + 3 cm
K = 12 cm
Jadi keliling segitiga tersebut adalah 12 cm.
2. Luas suatu segitiga adalah 96 cm². Jika panjang alasnya 12 cm, tentukan tinggi segitiga tersebut!
L = 96
L = ½at
96 = ½ x 12 x t
96 : ½ = 12 x t
192 = 12 x t
t = 192/12
t = 16 cm
3. Jika diketahui tinggi segitiga 4 cm dan alasnya 6 cm. Berapa luasnya?
Diketahui :
t = 4 cm
a = 6 cm
ditanya :
L . . . .?
Jawab :
L = ½ x a x t
L = ½ x 6 cm x 4 cm
L = 12 cm²
Jadi luas segitiga adalah 12 cm²
4. Diketahui keliling segitiga sama kaki adalah 16 cm. Jika panjang alasnya 6 cm, berapakah luasnya?
Panjang kedua buah 2 sisi miring = keliling – alas = 16 – 6 = 10 cm
Panjang masing-masing sisi miring = 10 : 2 = 5 cm
t² = 5² – 3² → 3 berasal dari ½ x alas
t² = 25 – 9
t² = 16
t = √16
t = 4 cm
L = ½ x 6 x 4 = 12 cm²
5. Sebuah taman berbentuk setitiga siku-siku dengan panjang sisinya masing-masing 3m, 4m, 5m. Jika separuh luas taman akan ditutup tegel keramik, dengan harga paving tiap meter perseginya Rp 100.000,00. Butuh biaya berapa untuk pemasangan tegel keramik yang menutup taman tersebut?
Jawab:
Untuk mengetahui separuh luas tegel keramik yang akan dipasang, maka kita perlu tahu luas setengah setiga siku-siku tersebut. Dengan demikian:
L= ½ luas setiga siku-siku=½ x ½ x a x t
L=1/4 x 4x 3= 3 m2
Biaya total yang dibutuhkan = Rp 100.000,00 x 3 = Rp 300.000,00
Jadi untuk memagari pinggiran taman dibutuhkan biaya sebesar Rp 300.000,00
6. Panjang sisi miring dan alas segitiga siku-siku berturut-turut adalah 20 cm dan 24 cm. Berapakah luas segitiga tersebut?
20² = t² + 12² → 12 berasal dari ½ panjang alas
t² = 20² – 12²
t² = 400 – 144
t² = 256
t = √256
t = 16 cm
L = ½ x 24 x 16 = 192 cm²
7. Diketahui luas dari sebuah segitiga yang panjang alasnya 24 cm adalah 180 cm2. Hitunglah tinggi dari segitiga tersebut!
Jawaban:
Luas Segitiga = ½ x alas x tinggi
180 cm2= ½ x 24 cm x tinggi
180 cm2= 12 cm x tinggi
tinggi = 180 cm2/12 cm
tinggi = 15 cm.
8. Pak Willy mengintari pinggiran lapangan berbentuk persegi panjang dua kali putaran penuh dan menempuh jarak 600 m. Jika lebar lapangan 50 m. Berapa luas lapangan tersebut?
Jawaban:
Untuk mencari luas lapangan, kita perlu tahu ukuran lapangan. Karena panjang lapangan belum diketahui, maka kita cari panjang lapangan dulu dengan konsep keliling yang sudah kita pelajari.
Karena mengelilingi dua kali putaran penuh, maka keliling lapangan 600m/2= 300 m.
Maka K=2p+2l
300=2p+2.50
300=2p+100
2p=200, maka p= 100m.
Jadi panjang lapangan 100m.
Dengan demikian luas lapangan= px l= 100 x 50= 500m2
9. Sebuah segitiga DEF yang merupakan segitiga sama sisi memiliki luas 25√3 cm², hitunglah berapa kelilingnya?
Penyelesaian :
Diketahui: luas = 25√3 cm²
Ditanya: keliling ?
Jawaban:
Luas = (a²/4)√3
25√3= (a²/4)√3 (√3 di ruas kanan dan ruas kiri bisa kita coret)
25 = a²/4
100 = a²
a = √100
a = 10 cm
Keliling = 3a
Keliling = 3.10
Keliling = 30 cm.
10. Diketahui segitiga ABC siku-siku di B. Jika Luasnya 150 cm² dan panjang AB 20 cm, hitunglah keliling segitiga tersebut!
Berdasarkan soal tersebut, AC adalah sisi miring segitiga.
L = ½ x AB x BC
150 = ½ x 20 x BC
150 : ½ = 20 x BC
300 = 20 x BC
BC = 300/20
BC = 15 cm
AC² = AB² + BC²
AC² = 20² + 15²
AC² = 400 + 225
AC² = 625
AC = √625
AC = 25 cm
K = AB + BC + AC = 20 + 15 + 25 = 60 cm
Tes Matematika Lainnya
- Tes Matematika: Otak Atik Otak – Jumlah nomor yang harus didapatkan: 50. Nomor yang diberikan: 2 8 9 15 20 40
- QUIZ Matematika Deret Aritmatika: jika 11 X 11 = 4, jadi 33 X 33 = ??
- Tes Matematika Menghitung Jumlah Segi Tiga
- QUIZ Matematika: Apel, Pisang dan Semangka
- Soal Tes Matematika Deret Angka
- Tes Matematika Logika Aritmetika: Jika 3 + 1 = 24, 5 + 2 = 37, Jadi 7 + 5 = ???
- Tes Matematika Deret Angka Untuk Yang Pintar – Tomat, Timun Dan Paprika
- Tes Matematika “Otak Atik Otak” Jumlah nomor yang harus didapatkan: 50 & Nomor yang diberikan: 2 8 9 15 20 40
- Tes Matematika Pengukuran Berat: Sebuah botol & tutupnya berberat 110g. Berat botol 100g lebih berat daripada tutupnya. Berapa berat tutupnya?
- Matematika Jika 2=6, 3=15, 4=24, 5=35, 6=48 Jadi 7=??
- Tes Matematika Pemecahan Masalah Logika Visual Psikotes Roda Gigi X – Beserta Rumus, Soal & Jawaban Untuk Menghitung Panjang Lintasan Roda
- Tes Matematika Volume: Menghitung Volume Solid Dalam Sebuah Ruang
Bacaan Lainnya
- Berapa Kecerdasan IQ Anda? Tes IQ Anda Disini
- 10 Kebiasaan Baik Yang Dapat Mengasah Otak Menjadi Lebih Efektif
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- Tulisan Menunjukkan Kepribadian Anda & Bagaimana Cara Anda Menulis?
- Top 10 Sungai Terpanjang Di Dunia
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “oooh begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing
