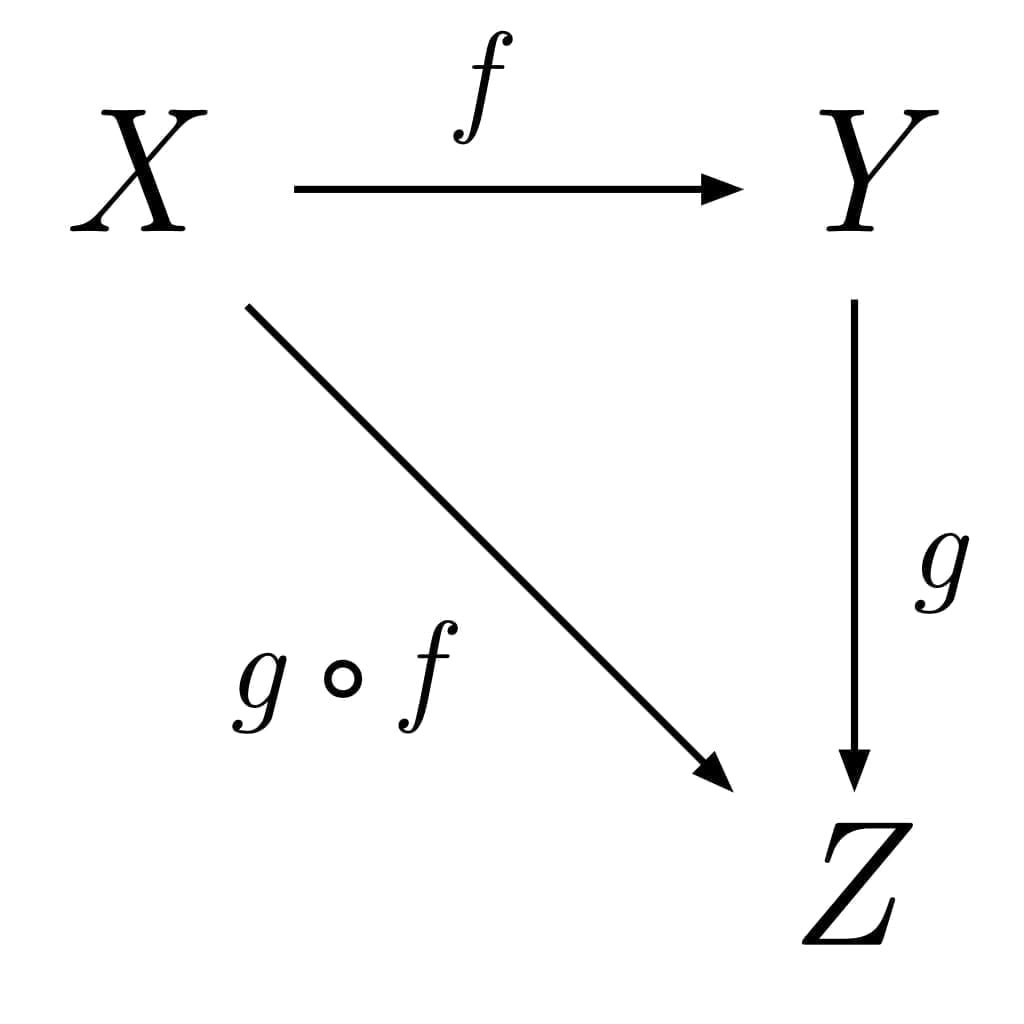Teori Kategori
Teori kategori sangat terkait dengan topologi aljabar. Topologi adalah cabang matematika yang mempelajari sifat-sifat benda geometris yang diawetkan dengan deformasi terus menerus tanpa robek atau menempel, seperti karet gelang yang dapat diregangkan tanpa putus.
Teori kategori dapat dipahami sebagai teori umum struktur matematika (struktur klasik misalnya grup, ring, modul, dan ruang topologi). Sifat struktur matematika, bagaimanapun, tidak didefinisikan melalui hubungan antara elemen dari himpunan pembawa (s), melainkan menggunakan morfisme dan fungsi, seolah-olah, melalui perbandingan baik di dalam maupun di antara kategori.
Elemen dasar
Studi kategori, sangat abstrak, dimotivasi oleh banyaknya karakteristik umum untuk berbagai kelas yang terkait dengan struktur matematika.
Berikut adalah contoh. Kelas grup Grp mencakup semua objek dengan “struktur grup”. Lebih tepatnya, Grp mencakup semua himpunan G yang memiliki relasi biner yang memenuhi himpunan aksioma tertentu. Dengan demikian, teorema dapat dibuktikan dengan membuat deduksi logis dari rangkaian aksioma ini. Misalnya, mereka memberikan bukti langsung bahwa elemen identitas suatu kelompok itu unik.
Alih-alih hanya mempelajari objek tunggal (kelompok) yang memiliki struktur tertentu, seperti yang selalu dilakukan oleh teori matematika, teori kategori menekankan morfisme dan proses yang mempertahankan struktur antara dua objek. Tampaknya dengan mempelajari morfisme ini seseorang dapat mempelajari lebih lanjut tentang struktur objek.
Dalam contoh kita, morfisme yang dipelajari adalah homomorfisme kelompok. Homomorfisme kelompok antara dua kelompok mempertahankan struktur kelompok dengan cara yang sangat tepat; itu adalah proses yang mengaitkan satu kelompok dengan yang lain, sambil mempertahankan semua informasi tentang struktur kelompok pertama di dalam kelompok kedua. Studi homomorfisme grup kemudian menyediakan alat untuk mempelajari sifat umum grup dan konsekuensi aksioma yang berkaitan dengan grup.
Hal yang sama dalam banyak teori matematika. Kategori adalah formulasi aksiomatik yang menghubungkan struktur matematika dengan fungsi yang melestarikannya. Sebuah studi sistematis kategori memungkinkan untuk membuktikan hasil umum dari aksioma kategori.
Kategori itu sendiri adalah jenis struktur matematika, di mana ada proses yang mempertahankan strukturnya. Proses seperti ini disebut functor.
Baca juga: Simbol Matematika Lengkap Beserta Artinya | Math Symbol
Contoh Teori Kategori
Dari pendefinisian kategori, terasa alami untuk mendefinisikan suatu kategori SET dengan Obj(SET) merupakan kelas yang berisi semua himpunan dan untuk sebarang himpunan A, B, ∉ Obj(SET) kita punyai Hom (A,B) fungsi dari himpunan A ke himpunan B. Perhatikan bahwa kategori SET bukanlah sebuah kategori kecil dikarenakan koleksi dari seluruh himpunan bukanlah suatu himpunan (untuk menghindari paradoks Russel)
Beberapa contoh lain dari kategori diberikan pada tabel berikut
| Kategori | Objek | Morfisma |
|---|---|---|
| Grp | Grup | Homomorfisma Grup |
| Manp | Manifold mulus | Pemetaan yang terdiferensialkan kontinu p-kali |
| Met | Ruang Metrik | Pemetaan metrik |
| R-Mod | R-Modul, dengan R suatu gelanggang | Homomorfisma modul |
| Ring | Gelanggang | Homomorfisma gelanggang |
| Top | Ruang Topologi | Fungsi kontinu |
| VectK | Ruang vektor atas lapangan K | Pemetaan linier |
Ada banyak contoh untuk teori kategori:
- Kategori (Ens), yang objeknya adalah himpunan, dan panahnya adalah pemetaan, dengan komposisi pemetaan yang biasa. Secara khusus, kita melihat bahwa objek dari suatu kategori tidak harus membentuk suatu himpunan!
- Kategori (Top), yang objeknya adalah ruang topologi, dan panah adalah pemetaan berkelanjutan, dengan komposisi biasa.
- Kategori (Met), yang objeknya adalah ruang metrik, dan panah adalah pemetaan kontinu yang seragam, dengan komposisi biasa.
- Kategori (Mon), yang objeknya adalah monoid dan panah adalah morfisme, dengan komposisi biasa.
- Kategori (Grp), yang objeknya adalah grup dan panah adalah morfisme, dengan komposisi yang biasa.
- Kategori (Ab), yang objeknya adalah grup abelian dan panah adalah morfisme, dengan komposisi biasa.
- Kategori (ACU), yang objeknya adalah cincin komutatif kesatuan dan panah adalah morfisme, dengan komposisi biasa.
- Kategori (Ord), yang objeknya diatur set dan panah meningkatkan peta.
Contoh sebelumnya memiliki satu properti yang sama: objek adalah set dengan struktur tambahan, dan panah selalu merupakan pemetaan antara set yang mendasarinya. Mereka adalah kategori konkret, yaitu kategori yang dilengkapi dengan fungsi yang setia pada kategori himpunan (dalam kasus ini, itu adalah fungsi yang terlupakan). Properti ini sangat istimewa. Berikut adalah contoh kategori tanpa properti ini:
- Monoid (M, *, e) dan kami mendefinisikan kategori M:
- objek: hanya satu
- panah: elemen monoid, semuanya dimulai dari satu objek untuk kembali ke sana;
- komposisi: diberikan oleh hukum monoid (identitasnya adalah panah yang terkait dengan e).
- Himpunan E, diberkahi dengan relasi refleksif dan transitif R, dan didefinisikan kategori terkait sebagai berikut:
- objek: elemen dari keseluruhan;
- panah: untuk semua objek e, dan f, terdapat panah dari e, ke f, jika dan hanya jika eRf, (dan sebaliknya tidak ada panah);
- komposisi: gabungan dua panah adalah satu-satunya panah yang menyatukan kedua ujungnya (hubungannya transitif); identitas adalah satu-satunya panah yang menghubungkan suatu objek dengan dirinya sendiri (relasinya bersifat refleksif).
Contoh ini sangat menarik dalam kasus berikut: himpunan adalah himpunan bukaan ruang topologi, dan relasinya adalah inklusi; ini memungkinkan untuk mendefinisikan pengertian preflight dan sheaf, melalui functors.
Bacaan Lainnya
- Simbol Infinity Tak Terhingga ∞
- Fungsi Matematika: Linear, Konstan, Identitas – Beserta Soal dan Jawaban
- Topologi Matematika – Contoh Soal dan Jawaban Ruang Topologi
- Rumus Matematika Keuangan – Contoh Soal dan Jawaban
- Induksi Matematika Rumus, Pembuktian, Deret, Keterbagian, Pertidaksamaan, Soal, Pembahasan dan Jawaban
- Rumus Dan Cara Menghitung Berat Badan Ideal (BMI)
- Tes Kepribadian Warna: Warna Mana Yang Anda Miliki? Hijau, Oranye, Biru, Emas
- Manusia Purba: Evolusi Manusia
- Di New York City, Anda dapat mengagumi “Manhattanhenge”
- Gunung Agung Di Bali
- Letusan Gunung Tambora Yang Sedikit Diketahui Padahal Sangat Berdampak Pada Iklim Planet Bumi
- Bagaimana Cara Menjalankan Mobil Dengan Bahan Bakar Jagung?
- Awalnya, reaktor nuklir pertama digunakan untuk produksi plutonium sebagai bahan senjata nuklir
- Sebagian Cabang Dari Biologi: Bioteknologi
- Bagaimana Menentukan Umur Batang Kayu? Anda Bisa Melihat Irisan Batang Kayu – Kambium
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan sering terdengar, jika Anda memasang aplikasiHP kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Cleverly Smart, math3ma, Stanford University, Joyal’s CatLab, Cole / Medium
Sumber foto: Wikimedia Commons (Public Domain)
Penjelasan foto: Teori kategori. Sebuah kategori dengan objek X, Y, Z, dan morfisme f, g, g ∘ f, dan tiga morfisma identitas (tidak ditunjukkan) 1X, 1Y, dan 1Z.
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing