Teorema Binomial

Binomial Newton adalah rumus matematika yang diberikan oleh Isaac Newton untuk menemukan perluasan pangkat bilangan bulat dari binomial. Ini juga disebut rumus binomial Newton, atau lebih sederhananya rumus teorema binomial.

Rumus binomial Newton adalah sebagai berikut: Untuk semua (a,b)∈K2 (dengan K himpunan real atau kompleks) dan untuk semua n∈N: (a+b)n=n∑k=0 (nk)akbn− k.

Bagaimana cara menghitung binomial Newton?

Jika a = b = 1, rumus binomial menjadi… ekspresi dari pangkat 2 (karena koefisien hanya dikalikan dengan 1). Kami juga memeriksanya di segitiga yang sangat ajaib ini. Ambil contoh n = 6 dan tambahkan nilai garisnya: 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 2⁶.

Dalam Aljabar, ekspresi binomial berisi dua istilah yang digabungkan dengan tanda penjumlahan atau pengurangan. Misalnya, (x + y) dan (2 – x) adalah contoh ekspresi binomial.

Terkadang, kita mungkin perlu memperluas ekspresi binomial seperti yang ditunjukkan di bawah ini.

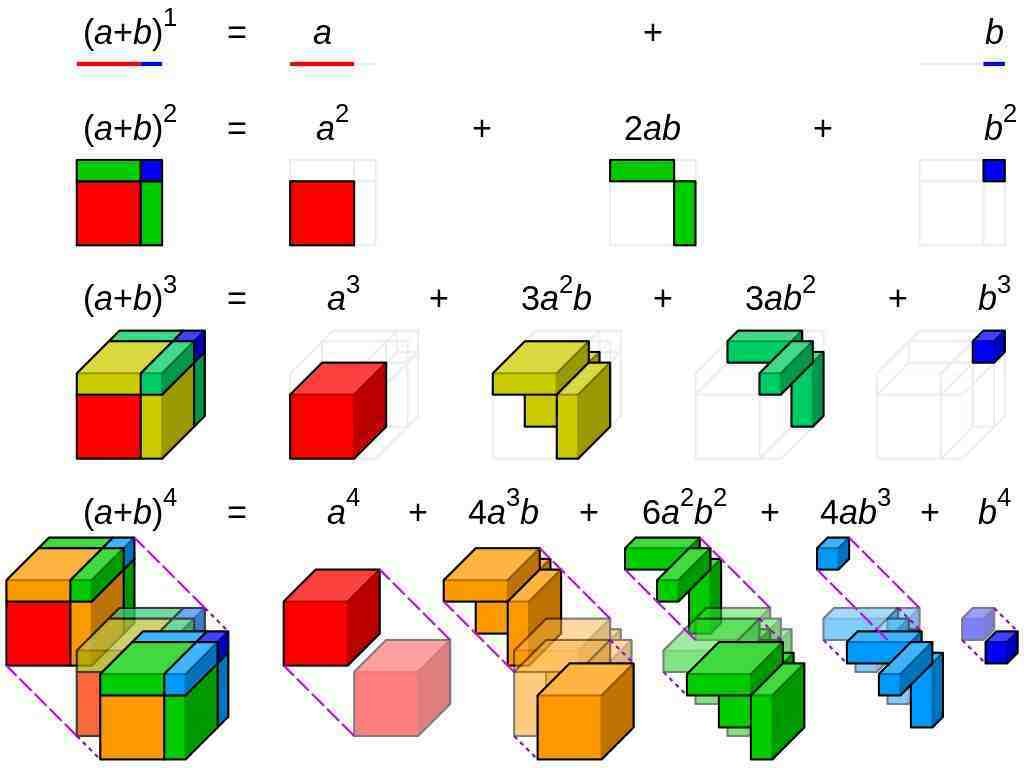
(a + b)⁰ = 1

(a + b)¹ = a + b

(a + b)² = a² + 2ab + b²

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Anda menyadari bahwa memperluas ekspresi binomial dengan perkalian langsung seperti yang ditunjukkan di atas cukup rumit dan tidak dapat diterapkan untuk eksponen yang lebih besar.

Pada artikel ini, kita akan belajar bagaimana menggunakan teorema Binomial untuk memperluas ekspresi binomial tanpa harus mengalikan semuanya.

Apa itu Teorema Binomial?

Jejak teorema binomial diketahui manusia sejak abad ke-4 SM. Binomial untuk kubus digunakan pada abad ke-6 M. Seorang matematikawan India, Halayudha, menjelaskan metode ini menggunakan segitiga Pascal pada abad ke-10.

Pernyataan yang jelas dari teorema ini dinyatakan pada abad ke-12. Para matematikawan membawa temuan ini ke tahap berikutnya sampai Sir Isaac Newton menggeneralisasi teorema binomial untuk semua eksponen pada tahun 1665.

Teorema Binomial menyatakan perluasan aljabar pangkat dari binomial, yang berarti polinomial (a+b)ⁿ dapat diekspansi menjadi beberapa suku.

Secara matematis, teorema ini dinyatakan sebagai:

(a + b)ⁿ = aⁿ+ (ⁿ₁) a^{n – 1}b¹ + (ⁿ₂) a^{n – 2}b² + (ⁿ₃) a^{n – 3}b³+ ………+ b ⁿ

yang dimana (ⁿ₁), (ⁿ₂), … adalah koefisien binomial.

Berdasarkan sifat-sifat Teorema Binomial di atas, kita dapat menurunkan Rumus Binomial sebagai:

(a + b)ⁿ = aⁿ+ na^{n – 1}b¹ + [n (n – 1)/2!] a^{n – 2}b² + [n (n – 1) (n – 2)/ 3!]a^{n – 3}b³+ ………+ b ⁿ

Atau, kita dapat menyatakan rumus Binomial sebagai:

(a + b)ⁿ = ⁿC₀aⁿ+ ⁿC₁a^{n – 1}b + ⁿC₂a^{n – 2}b²+ ⁿC₃a^{n – 3}b³+ ………. + ⁿC _nb ⁿ

Yang dimana (ⁿ_r) = ⁿC_r = n! / {r! (n – r)!} dan (C) dan (!) adalah kombinasi dan faktorial masing-masing.

Contoh:

3! = (3)(2)(1) =6
5! = (5)(4)(3)(2)(1) =120
4! /2! = (4)(3)(2)(1)/(2)(1) =12
¹⁰C₆= 10! / (10 – 6)! 6! = 10! / 4! 6! = (1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10) / 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 x 5 x 6 = 7 x 8 x 9 x 10 /1 x 2 x 3 x 4 = 7 x 3 x 10 = 210

Bagaimana cara menggunakan Teorema Binomial?

Ada beberapa hal yang perlu Anda ingat saat menerapkan Teorema Binomial.

Ini adalah:

Eksponen suku pertama (a) berkurang dari n ke nol
Eksponen dari suku kedua (b) meningkat dari nol menjadi n
Jumlah pangkat dari a dan b sama dengan n.
Koefisien suku pertama dan suku terakhir sama-sama 1.

Contoh soal dan jawaban Teorema Binomial

Contoh 1: Kembangkan (a + b)⁵

Jawaban:

⟹ (a + b)⁵ = aⁿ+ (⁵₁) a^{5– 1}b¹ + (⁵₂) a^{5 – 2}b² + (⁵₃) a^{5– 3}b³+ (⁵₄) a^{5– 4}b⁴+ b⁵

= a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Contoh 2: Kembangkan (x + 2)⁶ menggunakan rumus Binomial.

Jawaban:

Jika diberikan a = x;

b = 2 dan n = 6

Substitusikan nilai ke dalam rumus binomial

(a + b)ⁿ = aⁿ+ na^{n – 1}b¹ + [n (n – 1)/2!] a^{n – 2}b² + [n (n – 1) (n – 2)/ 3!]a^{n – 3}b³+ ………+ b ⁿ

⟹ (x + 2)⁶= x⁶+ 6x⁵(2)¹ + [(6)(5)/2!] (x⁴) (2²) + [(6)(5)(4)/3!] (x³) (2³) + [(6)(5)(4)(3)/4!] (x²) (2⁴) + [(6)(5)(4)(3)(2)/5!] (x) (2⁵) + (2)⁶

= x⁶ + 12x⁵ + 60x⁴+160x³ + 240x²+ 192x + 64

Contoh 3: Gunakan teorema binomial untuk memperluas (2x + 3)⁴

Jawaban:

Dengan membandingkan dengan rumus binomial, kita dapatkan,

a = 2x, b =3 dan n = 4.

Substitusikan nilai-nilai dalam rumus binomial.

⟹ (2x + 3)⁴= x⁴+ 4(2x)³(3) + [(4)(3)/2!] (2x)² (3)² + [(4)(3)(2)/4!] (2x) (3)³ + (3)⁴

= 16 x⁴ + 96x³+216x²+ 216x + 81

Contoh 4: Carilah perluasan dari (2x − y)⁴

Jawaban:

(2x − y)⁴ = (2x) + (−y)⁴ = (2x)⁴ + 4(2x)³ (−y) + 6(2x)²(−y)²+ 4(2x) (−y)³+ (−y)⁴

= 16x⁴ − 32x³y + 24x²y² − 8xy³ + y⁴

Contoh 5: Gunakan Teorema Binomial untuk memperluas (2 + 3x)³

Jawaban:

Dengan membandingkan dengan rumus Binomial,

a = 2; b = 3x dan n = 3

⟹ (2 + 3x)³ = 2³+ (³₁) 2²(3x)¹ + (³₂) 2(3x)² + (3x)³

= 8 + 36x + 54x²+ 27x³

Contoh 6: Kembangkan (x² + 2)⁶

Jawaban:
(x² +2)⁶ = ⁶C₀(x²)⁶(2)⁰ + ⁶C₁(x²)⁵(2)¹ + ⁶C₂(x²)⁴(2)² + ⁶C₃(x²)³(2)³ + ⁶C₄(x²)²(2)⁴ + ⁶C₅(x²)¹(2)⁵ + ⁶C₆(x²)⁰(2)⁶

= (1) (x¹²) (1) + (6) (x¹⁰) (2) + (15) (x⁸) (4) + (20) (x⁶) (8) + (15) (x⁴) (16) + (6) (x²) (32) + (1)(1) (64)

= x¹² + 12 x¹⁰ + 60 x⁸ + 160 x⁶ + 240 x⁴ + 192 x² + 64

Contoh 7: Perluas ekspresi (√2 + 1)⁵ + (√2 − 1)⁵menggunakan rumus Binomial.

Jawaban:

(x + y)⁵ + (x – y)⁵ = 2[5C₀ x⁵ + 5C₂ x³ y² + 5C₄ xy⁴]

= 2(x⁵+ 10 x³ y²+ 5xy⁴)

= (√2 + 1)⁵+ (√2 − 1)⁵= 2[(√2)⁵+ 10(√2)³(1)²+ 5(√2) (1)⁴]

=58√2

Contoh 8: pembuktian kombinatorik

Apabila kita ingin menggunakan pembuktian kombinatorik untuk membuktikan teorema tersebut dan pada suku – suku dan hasil dari penjabaran (x+y)^n (x+y)^n dan berbentuk xn – jy jx^n – jy^j untuk j = 0,1,2, … ,nj = 0,1,2, … , n.

Cara menghitung banyaknya pada suku yang berbentuk xn – jy^j xn – jy^j, yang pertama kita perlu memilih (n-j) (n-j) xx dan dari nn faktor.

Oleh karena itu pada koeefisien dari xn-jy^ jx^n-jy^j ialah (nn-j) (n-jn) yang pada ekuivalen dengan (nj) (jn).

Dibawah ini merupakan contoh cara penyeleseian untuk mengilustrasikan pada teorema yaitu :

Contoh:

Ada berapakah nilai pada koefisien dari x^12 y^13 pada ekspansi (x+y)^25 ?

Jawaban:

Dari teorema binomial, nilai koefisien x^12 y^13 dapat dihitung dengan.
(25/13) = 25!/ 13! 12! = 5.200.300.

Contoh:

Ada berapakah nilai dari koefisien x^12 y^13 pada ekspansi (2x – 3y) 25 (2x-3y) 25 ?

Jawaban:

Pertama yang perlu diingat bahwasannya ekspresi (2x- 3y) 25 (2x-3y) 25 = (2x+(-3y)) 25 (2x + (-3y)) 25, dengan berdasarkan teorema binomial ini kita dapatkan :

(2x + (-3y)) 25 = ∑j = 025 (25j) (2x) 25 – j(−3y)j

Akibatnya, koefisien x12y13x12y13 pada ekspansi (2x+(−3y)) 25 (2x + (−3y)) 25 dan dapat diperoleh dengan j = 13^j = 13, yaitu :

(25/13) 2^12 (−3)^13 = − 25!/13! 12! 2^12 3^13

Rumus Aljabar – Operasi Rumus Perhitungan, Penjelasan, Contoh Soal dan Jawaban

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: CleverlySmart, Cue Math, Math is Fun

Sumber foto: Author: Cmglee (CC BY-SA 3.0) via Wikimedia Commons

Penjelasan foto: visualisasi ekspansi binomial hingga pangkat ke-4.

Teorema Binomial (Aljabar) | Binomial Newton

Teorema Binomial

Bagaimana cara menghitung binomial Newton?

Terkadang, kita mungkin perlu memperluas ekspresi binomial seperti yang ditunjukkan di bawah ini.

Apa itu Teorema Binomial?

Teorema Binomial menyatakan perluasan aljabar pangkat dari binomial, yang berarti polinomial (a+b)ⁿ dapat diekspansi menjadi beberapa suku.