Sudut

Sudut matematika dalam geometri adalah besaran rotasi suatu ruas garis dari satu titik pangkalnya ke posisi yang lain. Selain itu, dalam bangun dua dimensi yang beraturan, sudut dapat pula diartikan sebagai ruang antara dua buah ruas garis lurus yang saling berpotongan.

Besar sudut pada lingkaran 360°. Besar sudut pada segitiga siku-siku 180°. Besar sudut pada persegi/segi empat 360°. Untuk mengukur sudut dapat digunakan busur derajat. Tiap sudut segitiga sama sisi masing masing 60°, karena semua sudutnya sama besar maka 180° :3 = 60°. Sedangkan tiap sudut persegi 90° karena semua sudutnya juga sama besar maka 360° : 4 = 90°

Nama Sudut (Matematika)

Memberi nama untuk sudut matematika dengan berbagai karakteristik:

Sudut 0 tidak memiliki jarak antara kedua garis.
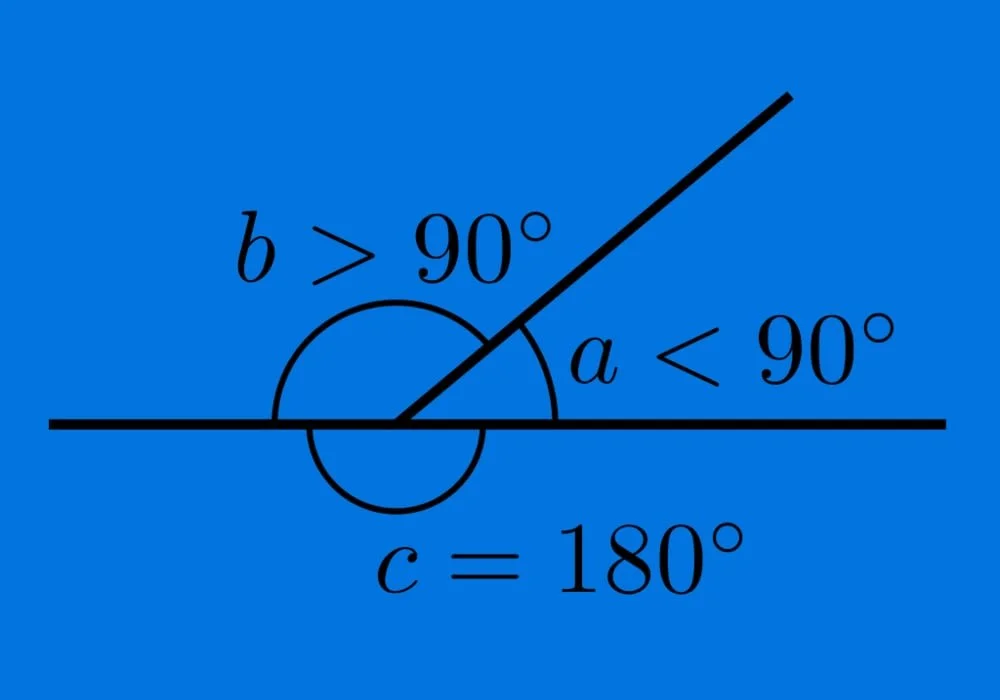
Sudut lancip adalah sudut antara 0 dan 89°
Sudut siku-siku adalah sudut 90%. Dua garis yang membentuk sudut 90% jika tegak lurus dengan yang lain.Pembentukan simbol sudut adalah potongan kotak. Simbol itu menunjukkan jika kamu bekerja dengan sudut siku-siku.
Sudut tumpul adalah sudut antara 91 dan 179°
Sudut lurus adalah sudut yang besarnya 180°
Sudut pusat adalah sudut yang memiliki titik sudut yang terletak ditengah lingkaran.
Sudut bersebelahan adalah sudut yang memiliki titik sudut yang sama dan satu bagian sisi yang sama(bersebelahan berarti dekat).
Sudut yang berseberangan dibentuk oleh 2 garis lurus menyilang dan selalu sama.

Sudut 90°

Sudut yang sering digunakan dalam perdagangan adalah sudut 90. Itu dapat membantu dalam pemahaman mengapa demikian. Jika 2 garis disilangkan, maka membentuk 4 sudut. Jumlah dari keempat sudut itu adalah 360.

Garis utama dari jangka adalah 2 garis lurus yang mana jika 2 garis tersebut disilangkan masing-masing besar sudutnya adalah 90. Sebagian besar dan perusahaan-perusahaan mengatakan untuk membuat garis sepanjang garis utama dari jangka.

Jika 2 garis disilangkan, dari keempat sudut yang terbentuk masing-masing besarnya sama jika pada setiap sudutnya besarnya 90. Sudut 90 biasa disebut sudut siku-siku. Sudut siku-siku biasanya terdapat pada bangun datar seperti segitiga siku-siku, persegi panjang dan persegi.

Radian

Radian adalah satuan sudut dalam bidang yang dilambangkan dengan “rad”. Satuan sudut ini pernah masuk dalam kategori satuan tambahan SI yang kemudian kategori ini tidak lagi sejak tahun 1995 dan saat ini radian dianggap sebagai satuan turunan dalam SI.

Satu radian atau 1 rad adalah besarnya sudut yang dibentuk oleh dua buah jari-jari lingkaran berjari-jari 1 meter dan membentuk busur sepanjang juga 1 meter. Atau dalam gambar di samping r = b = 1 meter.

Panjang busur suatu lingkaran dapat dihitung langsung dengan mengalikan besarnya sudut dengan jari-jari lingkaran, apabila besarnya sudut telah dalam satuan radian.

**Ilustrasi ukuran sudut**
Panjang busur $L\!$ (meter)	Sudut $\theta\!$ (rad)
$R\!$	$1\!$
${\frac {1}{4}}{\hbox{O}}$	${\frac {\pi }{2}}$
${\frac {1}{2}}{\hbox{O}}$	$\pi \!$
${\frac {3}{4}}{\hbox{O}}$	${\frac {3\pi }{2}}$
${\hbox{O}}\!$	$2\pi \!$
$\theta R\!$	$\theta\!$

{\hbox{O}}\!

dibaca lingkaran.

Radian dengan Derajat

$1{\mbox{radian}}=1\cdot {\frac {180{\mbox{derajat}}}{\pi }}$

$1{\mbox{derajat}}=1\cdot {\frac {\pi }{180{\mbox{derajat}}}}{radian}$

Contoh sudut matematika. Sumber foto: Wikimedia Commons

Diameter Sudut

Diameter angular

Diameter sudut adalah “diameter visual” suatu objek yang diukur sebagai sudut. Diameter visual adalah diameter dari proyeksi perspektif objek pada bidang melalui pusatnya yang tegak lurus dengan arah pandangan.

Rumus untuk menentukan diameter sudut adalah:

\delta =2\arctan \left({\frac {1}{2}}\,d/D\right),

dengan $\delta$ sebagai diameter sudut, dan $d$ dengan $D$ sebagai diameter visual dan jarak ke objek, dinyatakan dalam satuan yang sama. Jika $D$ lebih besar dari $d$ , $\delta$ dapat dihitung dengan rumus $\delta =d/D$ , yang hasilnya dalam radian (jari-jari).

Untuk objek bola yang diameter aktualnya sama dengan $d_{\mbox{act}}$ , diameter sudut dapat dicari dengan rumus

\delta =2\arcsin \left({\frac {1}{2}}\,d_{\mbox{act}}/D\right);

untuk kegunaan praktik, pembedaan antara $d$ dan $d_{\mbox{act}}$ hanya menimbulkan perbedaan pada objek bola yang relatif dekat.

Sudut Istimewa

Berikut ini nilai sudut matematika: sin, cos, dan tan untuk sudut istimewa:

Konversi Sudut

**Konversi Sudut Umum**
Sudut	Radians	Derajat	Gradians (Gons)
0	0	0°	0^g
1/24	$π$ /12	15°	16 2/3^g
1/12	$π$ /6	30°	33 1/3^g
1/10	$π$ /5	36°	40^g
1/8	$π$ /4	45°	50^g
1/2 $π$	1	c. 57.3°	c. 63.7^g
1/6	$π$ /3	60°	66 2/3^g
1/5	2 $π$ /5	72°	80^g
1/4	$π$ /2	90°	100^g
1/3	2 $π$ /3	120°	133 1/3^g
2/5	4 $π$ /5	144°	160^g
1/2	$π$	180°	200^g
3/4	3 $π$ /2	270°	300^g
1	2 $π$	360°	400^g

Contoh Soal Sudut Matematika

1. Sebuah kipas angin berputar dengan kecepatan 36 putaran per menit. Nyatakan kecepatan putaran kipas angin tersebut ke dalam satuan radian per detik!

Penyelesaian:
36 putaran/menit = 36 x 2π/60 putaran/detik
36 putaran/menit = 1,2π putaran/detik

Jadi 36 putaran per menit sama dengan 1,2π putaran per detik.

2. Nyatakan sudut matematika 50° dan 89° ke dalam radian!

Penyelesian:
50° = 50° x π/180°
50° = 0,277π
50° = 0,277 (3,14)
50° = 0,87 radian

89° = 89° x π/180°
89° = 0,494π
89° = 0,494 (3,14)
89° = 1,55 radian

3. Hitunglah jari-jari suatu lingkaran jika panjang busurnya 10 cm dan sudut pusatnya 36°!

Penyelesaian:
θ = 36°, maka:
36° = 36°xπ/180°
36° = 0,2π
Kita ketahui bahwa :
r = s/θ
r = 10 cm/0,2π
r = 10 cm/0,628
r = 15,9 cm

4. Nyatakan sudut matematika 0,45 radian dan 0,89 radian ke dalam satuan derajat!

Penyelesaian:
0,45 radian = 0,45 x 180°/π
0,45 radian = 25,80°

0,89 radian = 0,89 x 180°/π
0,89 radian = 51,02°

5. Nyatakan besar sudut matematika berikut ke dalam satuan radian!
a. 30° 20′ 15”
b. 106° 20′

Penyelesaian:
a. kita ketahui bahwa:
1” = (1/3600)°
1′ = (1/60)°
1° = 0,0174 radian, maka:
30° 20′ 15”
= 30° + 20.(1/60)° + 15.(1/3600)°
= (108000/3600)° + (1200/3600)° + (15/3600)°
= (109215/3600)°
= (109215/3600).0,0174 radian
= 0,53 rad

b. kita ketahui bahwa:
1′ = (1/60)°
1° = 0,0174 radian, maka:
106° 20′ = 106° + 20.(1/60)°
106° 20′ = (318/3)° + (1/3)°
106° 20′ = (319/3)°
106° 20′ = (319/3).0,0174 radian
106° 20′ = 1,85 rad.

6. Tentukanlah nilai dari $\sin 120^{\circ}+\cos 201^{\circ}+\cos 315^{\circ}$ !

Jawab:

$\sin 120^{\circ}$ berada pada kuadran 2, sehingga nilainya tetap positif dengan besar sama seperti $\sin 120^{\circ} = \sin (180-60)^{\circ} = \sin 60^{\circ} = \frac{1}{2} \sqrt{3}$

$\cos 120^{\circ}$ berada pada kuadran 3, sehingga nilainya negatif dengan besar sama seperti $\cos 120^{\circ} = \cos (180+30)^{\circ} = - \cos 30^{\circ} = - \frac{1}{2} \sqrt{3}$

$\cos 315^{\circ}$ berada pada kuadran 4, sehingga nilainya positif dengan besar sama seperti $\cos 315^{\circ} = \cos (360-45)^{\circ} = \cos 45^{\circ} = \frac{1}{2} \sqrt{2}$

Jadi $\sin 120^{\circ}+\cos 201^{\circ}+\cos 315^{\circ}=\frac{1}{2} \sqrt{3} - \frac{1}{2} \sqrt{3}+\frac{1}{2} \sqrt{2}=\frac{1}{2} \sqrt{2}$

7. Sebuah sudut lurus seperti gambar di atas dibagi menjadi dua buah sudut A dan sudut B. Jika perbandingan dari A dan B adalah 4 : 5, berapakah besar masing-masing sudut itu?

Penjelasan dan jawaban:

Diketahui: Perbandingan sudut A dan B = 4 : 5
Ditanya: Besar sudut masing-masing…??

Jawaban:

Ada beberapa langkah dasar yang harus dilakukan ketika menjawab soal dengan perbandingan seperti ini.

Langkah yang harus dilakukan :

1. Menetapkan besar sudut sebenarnya
2. Mencari nilai dari perbandingan dengan cara “n”
3. Mencari besar sudutnya masing.

Itulah gambaran langkah umumnya..
Kita langsung mulai dari yang pertama..

Cara 1. Menetapkan besar sudut sebenarnya

Perbandingan kedua sudut A dan B adalah 4 : 5.

Ini artinya perbandingan sudut A = 4, dan perbandingan sudut B = 5.

Besar sudut A sebenarnya adalah 4n
Besar sudut B sebenarnya adalah 5n.

Inilah yang disebut dengan cara “n”

Cara 2. Mencari nilai “n”

Kedua sudut membentuk sudut lurus, maka..

Sudut A + Sudut B = 180

4n + 5n = 180
9n = 180
n = 180 : 90
n = 20

Cara 3. Mencari besar sudut masing-masing

Nilai “n” sudah didapatkan…

Sekarang saatnya untuk mencari besar sudut A dan B.

Sudut A = 4n

Sudut A = 4 x n
Sudut A = 4 x 20
Sudut A = 80

Sudut B = 5n

Sudut B = 5 x n
Sudut B = 5 x 20
Sudut B = 100.

Jadi besar sudut A dan B masing-masing adalah 80 dan 100 derajat.

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math is Fun, Math Open Reference

Sudut Matematika dan Radian – Geometri – Soal Jawaban

Sudut

Nama Sudut (Matematika)

Sudut 0 tidak memiliki jarak antara kedua garis.

Sudut lancip adalah sudut antara 0 dan 89°

Sudut siku-siku adalah sudut 90%. Dua garis yang membentuk sudut 90% jika tegak lurus dengan yang lain.Pembentukan simbol sudut adalah potongan kotak. Simbol itu menunjukkan jika kamu bekerja dengan sudut siku-siku.

Sudut tumpul adalah sudut antara 91 dan 179°

Sudut lurus adalah sudut yang besarnya 180°

Sudut pusat adalah sudut yang memiliki titik sudut yang terletak ditengah lingkaran.

Sudut bersebelahan adalah sudut yang memiliki titik sudut yang sama dan satu bagian sisi yang sama(bersebelahan berarti dekat).

Sudut yang berseberangan dibentuk oleh 2 garis lurus menyilang dan selalu sama.

Sudut 90°

Radian

Radian dengan Derajat

Diameter Sudut

Sudut Istimewa

Konversi Sudut

Contoh Soal Sudut Matematika

1. Sebuah kipas angin berputar dengan kecepatan 36 putaran per menit. Nyatakan kecepatan putaran kipas angin tersebut ke dalam satuan radian per detik!

2. Nyatakan sudut matematika 50° dan 89° ke dalam radian!

3. Hitunglah jari-jari suatu lingkaran jika panjang busurnya 10 cm dan sudut pusatnya 36°!

4. Nyatakan sudut matematika 0,45 radian dan 0,89 radian ke dalam satuan derajat!

5. Nyatakan besar sudut matematika berikut ke dalam satuan radian!
a. 30° 20′ 15”
b. 106° 20′

6. Tentukanlah nilai dari $\sin 120^{\circ}+\cos 201^{\circ}+\cos 315^{\circ}$ !

7. Sebuah sudut lurus seperti gambar di atas dibagi menjadi dua buah sudut A dan sudut B. Jika perbandingan dari A dan B adalah 4 : 5, berapakah besar masing-masing sudut itu?

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

Sudut Matematika dan Radian – Geometri – Soal Jawaban

Sudut

Nama Sudut (Matematika)

Sudut 0 tidak memiliki jarak antara kedua garis.

Sudut lancip adalah sudut antara 0 dan 89°

Sudut siku-siku adalah sudut 90%. Dua garis yang membentuk sudut 90% jika tegak lurus dengan yang lain.Pembentukan simbol sudut adalah potongan kotak. Simbol itu menunjukkan jika kamu bekerja dengan sudut siku-siku.

Sudut tumpul adalah sudut antara 91 dan 179°

Sudut lurus adalah sudut yang besarnya 180°

Sudut pusat adalah sudut yang memiliki titik sudut yang terletak ditengah lingkaran.

Sudut bersebelahan adalah sudut yang memiliki titik sudut yang sama dan satu bagian sisi yang sama(bersebelahan berarti dekat).

Sudut yang berseberangan dibentuk oleh 2 garis lurus menyilang dan selalu sama.

Sudut 90°

Radian

Radian dengan Derajat

Diameter Sudut

Sudut Istimewa

Konversi Sudut

Contoh Soal Sudut Matematika

1. Sebuah kipas angin berputar dengan kecepatan 36 putaran per menit. Nyatakan kecepatan putaran kipas angin tersebut ke dalam satuan radian per detik!

2. Nyatakan sudut matematika 50° dan 89° ke dalam radian!

3. Hitunglah jari-jari suatu lingkaran jika panjang busurnya 10 cm dan sudut pusatnya 36°!

4. Nyatakan sudut matematika 0,45 radian dan 0,89 radian ke dalam satuan derajat!

5. Nyatakan besar sudut matematika berikut ke dalam satuan radian! a. 30° 20′ 15” b. 106° 20′

7. Sebuah sudut lurus seperti gambar di atas dibagi menjadi dua buah sudut A dan sudut B. Jika perbandingan dari A dan B adalah 4 : 5, berapakah besar masing-masing sudut itu?

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

5. Nyatakan besar sudut matematika berikut ke dalam satuan radian!
a. 30° 20′ 15”
b. 106° 20′