Vektor (Spasial)
Vektor spasial atau vektor Euclidean; biasa disebut vektor dalam matematika dan fisika adalah objek geometri yang memiliki besar dan arah.
Vektor dalam matematika dan fisika adalah objek geometri yang memiliki besar dan arah. Vektor jika dilambangkan dengan tanda panah (→). Besar vektor proporsional dengan panjang panah dan arahnya bertepatan dengan arah panah. Vektor dapat melambangkan perpindahan dari titik A ke B. Vektor sering ditandai sebagai
- AB→.
Vektor berperan penting dalam fisika: posisi, kecepatan dan percepatan objek yang bergerak dan gaya dideskripsikan sebagai vektor.
Panjang Vektor (Spasial)
Untuk mencari panjang sebuah vektor dalam ruang euklidian tiga dimensi, dapat digunakan cara berikut:
- ‖a‖=a12+a22+a32
yang merupakan konsekuensi dari Teorema Pythagoras karena vektor dasar e1, e2, e3 merupakan vektor-vektor satuan ortogonal. Ini sama dengan akar pangkat dua produk titik dari vektor itu sendiri:
- ‖a‖=a⋅a.
Vektor satuan (unit vector)
“Vektor satuan” (unit vector) adalah suatu vektor dengan panjang “satu”. Biasanya vektor satuan hanya digunakan untuk menunjukkan arah. Suatu vektor dengan panjang sembarang dapat dibagi oleh panjang untuk mendapatkan vektor satuan. Ini dikenal sebagai “normalisasi” (normalizing) suatu vektor. Suatu vektor satuan sering diindikasikan dengan sebuah “topi” di atas huruf “a” kecil sebagaimana pada â. Untuk menormalisasi suatu vektor a = [a1, a2, a3], bagilah vektor itu dengan panjangnya ||a||. Jadi:
- a^=a‖a‖=a1‖a‖e1+a2‖a‖e2+a3‖a‖e3
Vektor nol (null vector)
“Vektor nol” (null vector atau zero vector) adalah suatu vektor yang panjangnya “nol”. Penulisan dalam koordinat vektor ini adalah (0,0,0), dan biasanya diberi lambang 0→

Kesamaan dua vektor
Dua buah vektor dikatakan sama apabila keduanya memiliki panjang dan arah yang sama.
Kesejajaran dua vektor
Dua Buah Vektor disebut sejajar (paralel) apabila garis yang merepresentasikan kedua buah vektor sejajar.
Operasi vektor
Perkalian skalar
Sebuah vektor dapat dikalikan dengan skalar yang akan menghasilkan vektor juga, vektor hasil adalah:
- ra=(ra1)i+(ra2)j+(ra3)k
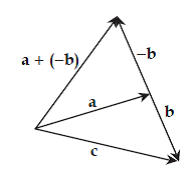
Penambahan vektor dan pengurangan vektor
Sebagai contoh vektor a=a1i + a2j + a3k dan b=b1i + b2j + b3k. Hasil dari a ditambah b adalah:
- a+b=(a1+b1)i+(a2+b2)j+(a3+b3)k
pengurangan vektor juga berlaku dengan cara mengganti tanda + menjadi tanda –
Vektor satuan
Vektor satuan adalah vektor yang memiliki panjang 1 satuan panjang. Vektor satuan dari sebuah vektor dapat dicari dengan cara:
- a^=a‖a‖=a1‖a‖i^+a2‖a‖j^+a3‖a‖k^
Operasi Aljabar pada Vektor
Penjumlahan dan penguraangan vektor
Secara geometri penjumlahan vektor dapat dilakukan dengan dua cara yaitu sebagai berikut
- Cara segitiga titik pangkal vektor
berimpit ruas dengan titik ujung vektor
. Jumlah vektor
dan
didapat dengan menarik ruas garis dari titik pangkal vektor
ke titik ujung vektor
. Ruas garis ini diwakili oleh vektor
. Sehingga
.

- Aturan jajar genjang Titik pangkal vektor
dan
harus berimpit.
 Jika vektor
Jika vektor dan
di R2
 Jika menggunakan pasangan terurut
Jika menggunakan pasangan terurut +
= (a1 + b1, a2 + b2)
–
= (a1 – b1, a2 – b2)
Perkalian Vektor
- Perkalian skalar dengan vektor Jika k skalar tak nol dan vektor
= a1 i + a2 j + a3 k maka vektor k
= (ka1, ka2, ka3).
- Perkalian skalar dua vektor Jika vektor
= a1 i + a2 j + a3 k dan vektor
= b1 i + b2 j + b3 k maka
.
= a1 b1 + a2b2 + a3b3
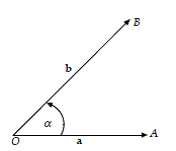
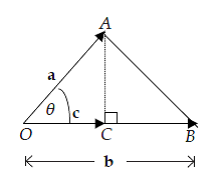
- Perkalian skalar dua vektor jika membentuk sudut
 Jika
Jika dan
vektor tak nol dan sudut α diantara vektor
dan
. Maka perkalian skalar vektor
dan
adalah . = |
|.|
| cos α
Sifat Operasi Aljabar Pada Vektor
Baca juga: Rumus Aljabar | Operasi Rumus Perhitungan, Penjelasan, Contoh Soal dan Jawaban
Hubungan Vektor Dengan Vektor Lain
Saling Tegak Lurus
Jika tegak lurus antara vektor dengan vektor
maka
.
= 0
Sejajar
Jika vektor sejajar dengan vektor
kalau
= β
dengan syarat β ≠ 0 Jika β > 0 dua vektor tersebut searah Jika β < 0 dua vektor saling berlawanan arah
Sudut Dua Vektor
Jika vector (a1, a2, a3) dan vektor (b1, b2, b3) sudut yang dapat dibentuk dari kedua vektor terbut adalah 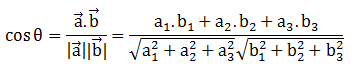
Proyeksi vektor
- Panjang proyeksi vektor a pada vektor b adalah
- Proyeksi vektor a pada vektor b adalah vektor
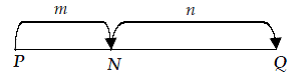
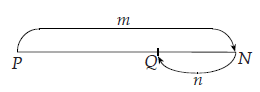
Perbandingan vektor
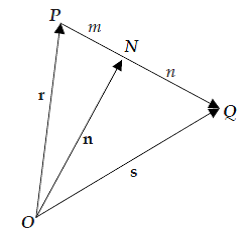
 Perbandingan PN : NQ = m : n terdapat dua jenis, yaitu:
Perbandingan PN : NQ = m : n terdapat dua jenis, yaitu:
Contoh Soal Vektor (spasial) dan Jawaban
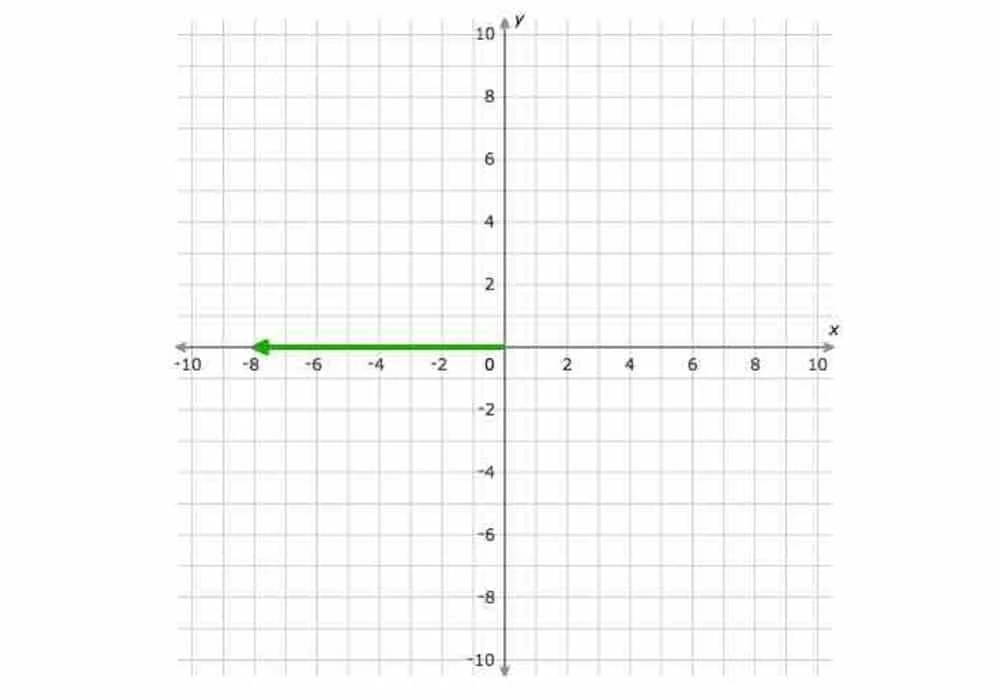
1. Temukan besarnya vektor. Tulis jawaban Anda dalam bentuk yang disederhanakan:
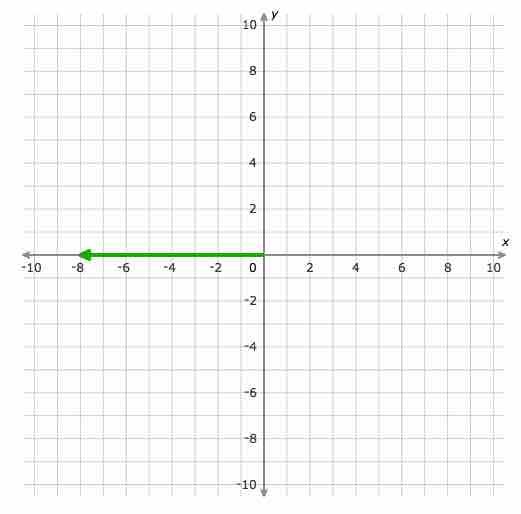 Jawaban: 8. Penjelasan: untuk menemukan besarnya vektor, pertama cari titik awalnya di dasar panah dan titik terminalnya di ujung panah. Titik awalnya adalah (0,0) dan titik terminalnya adalah (-8,0). Karena koordinat y dari titik awal (0,0) dan titik terminal (-8,0) sama, vektornya horizontal. Jadi, besarnya adalah nilai absolut dari perbedaan koordinat x, yaitu | -8-0 | = 8.
Jawaban: 8. Penjelasan: untuk menemukan besarnya vektor, pertama cari titik awalnya di dasar panah dan titik terminalnya di ujung panah. Titik awalnya adalah (0,0) dan titik terminalnya adalah (-8,0). Karena koordinat y dari titik awal (0,0) dan titik terminal (-8,0) sama, vektornya horizontal. Jadi, besarnya adalah nilai absolut dari perbedaan koordinat x, yaitu | -8-0 | = 8.
2. Vektor-vektor u, v, dan w tak nol dan | u | = | v |, Jika | v-w | = | u-w | maka…
A. u.v = | w |
B.
C. | u-w | = | v |
D. u – v tegak lurus w E. u + v tegak lurus w
Pembahasan:
Diketahui: | v – w | = | u – w | Kedua sisi di akarkan v.v + w.w – 2v.w = u.u + w.w – 2 u.w |v|2 + |w|2 – 2v.w = |u|2 + |w|2 – 2u.w
Dari soal diketahui | u | = | v | maka v.w = u.w u.w – v.w = 0 (u.w).w = 0 Karena perkaliannya = 0 maka (u-v) tegak lurus w.
Jawaban: D
3. Diketahui vektor-vektor 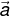 = (2, 2, z),
= (2, 2, z), 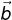 = (-8, y, -5) ,
= (-8, y, -5) , 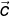 = (x, 4y, 4) dan
= (x, 4y, 4) dan 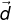 = (2x, 22, -z, 8). Jika vektor
= (2x, 22, -z, 8). Jika vektor 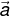 tegak lurus dengan vektor
tegak lurus dengan vektor 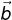 dan vektor
dan vektor 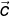 sejajar dengan
sejajar dengan 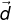 maka (y+z) =
maka (y+z) =
A. -5
B. -1
C. 1
D. 2
E. 5
Jawaban: C
4. Jika vektor 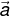 dan
dan 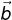 merupakan (
merupakan (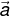 +
+ 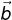 ).
).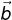 = 12 , |
= 12 , |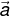 | = 2 dan |
| = 2 dan |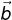 | = 3 maka sudut antara
| = 3 maka sudut antara 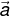 dan
dan 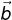 adalah….
adalah….
A. 60°
B. 45°
C. 300
D. 250
E. 200
Pembahasan:
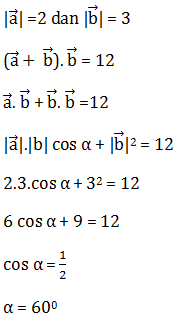
Jawaban: A
5. Misalkan A(t² + 1, t) dan B(1, 2), sehingga panjang vektor proyeksi  terhadap
terhadap  kurang dari
kurang dari  , maka nilai
, maka nilai t yang mungkin adalah…
Jawaban:
Proyeksi vektor terhadap

Jadi nilai t yang mungkin -3 < t < 1
catatan:
Panjang proyeksi vektor a terhadap b
Jika vektor a = (a1, a2, a3) dan vektor b = (b1, b2, b3)
Jika vektor a = (a1, a2, a3) maka panjang vektor a
6. Diketahui 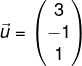 dan vektor
dan vektor 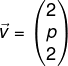 . Jika proyeksi skalar orthogonal
. Jika proyeksi skalar orthogonal  pada arah vektor
pada arah vektor 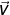 sama dengan setengah panjang vektor
sama dengan setengah panjang vektor 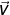 maka nilai p = …
maka nilai p = …
A. -4 atau -2
B. -4 atau 2
C. 4 atau -2
D. 8 atau -1
E. -8 atau 1
Pembahasan:

Jawaban: B
7. Diketahui vektor  dan vektor
dan vektor  membentuk sudut
membentuk sudut  . Jika panjang proyeksi
. Jika panjang proyeksi  pada
pada  sama dengan empat kali panjang
sama dengan empat kali panjang  , maka perbandingan panjang
, maka perbandingan panjang  terhadap panjang
terhadap panjang  adalah…
adalah…
Jadi perbandingan panjanga vektor terhadap vektor
adalah
8. Jika u dan v adalah vektor-vektor sehingga ||u|| = 5, ||v|| = 3 dan u . v = -1, maka ||u – v|| = …
Jawaban:
Panjang dari selisih dua vektor
Jadi ||u – v|| = 6
catatan:
Hasil kali perkalian titik dua vektor u dan v
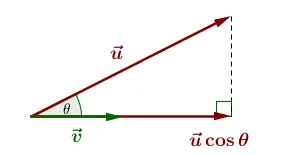
9. Diketahui persegi panjang ABCD dan D titik tengah OA, CD memotong diagonal AB di P. Jika  dan
dan  , maka
, maka  dapat dinyatakan sebagai…
dapat dinyatakan sebagai…

Jawaban:
Diketahui ,
dan dari gambar diketahui bahwa
sehingga
Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar
- Berapa Kecerdasan IQ Anda? Tes IQ Anda Disini
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- Tulisan Menunjukkan Kepribadian Anda & Bagaimana Cara Anda Menulis?
- Penyakit yang dapat dicegah dengan vaksin – Wajib diketahui
- Top 10 Sungai Terpanjang Di Dunia
- Tempat Wisata Yang Wajib Dikunjungi Di Indonesia Dan Luar Negri
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
- Bentuk Kaki Menandakan Karakter Anda – Bentuk Kaki nomer berapa yang Anda miliki?
Tentang Matematika
- Induksi Matematika Rumus, Pembuktian, Deret, Keterbagian, Pertidaksamaan, Soal, Pembahasan dan Jawaban
- Rumus Trigonometri Dan Contoh-Contoh Soal Beserta Jawabannya
- Tes Matematika Deret Angka Untuk Yang Pintar – Tomat, Timun Dan Paprika
- Tes Matematika “Otak Atik Otak” Jumlah nomor yang harus didapatkan: 50 & Nomor yang diberikan: 2 8 9 15 20 40
- Tes Matematika Pengukuran Berat: Sebuah botol & tutupnya berberat 110g. Berat botol 100g lebih berat daripada tutupnya. Berapa berat tutupnya?
- Matematika Jika 2=6, 3=15, 4=24, 5=35, 6=48 Jadi 7=??
- Tes Matematika Pemecahan Masalah Logika Visual Psikotes Roda Gigi X – Beserta Rumus, Soal & Jawaban Untuk Menghitung Panjang Lintasan Roda
- Rumus Trigonometri Dan Contoh-Contoh Soal Beserta Jawabannya
- Soal Rumus Kimia Hidrat (Air Kristal) Dan Jawabannya
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita! Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Wikipedia
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing







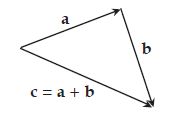
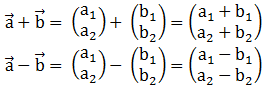


Klo soalnya
Tentukan vektor vektor berikut U=2,-22 v=1,-34 w=3,6,4