PINTERpandai
Pinter Pandai

Rumus Trigonometri Invers Beserta Contoh Soal dan Jawaban (arckosinus, arctangen, arckotangen, arcsekan, arckosekan)

2 min read

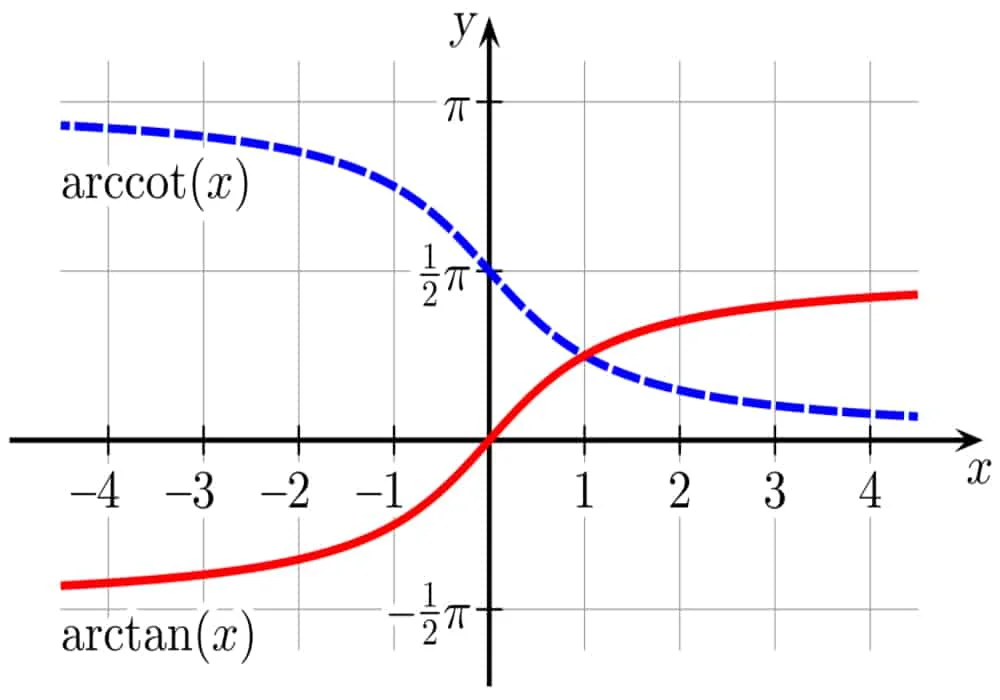
Trigonometri invers arctangent arccotangent

Fungsi Trigonometri Invers

Fungsi trigonometri invers adalah fungsi invers suatu fungsi trigonometri (dengan domain atau ranah yang terbatas). Dalam kata lain, fungsi trigonometri invers adalah fungsi invers suatu fungsi sinus, kosinus, tangen, kotangen, sekan dan kosekan, dan digunakan untuk mencari suatu sudut dari rasio trigonometri sudut yang lain. Fungsi trigonometri invers sering digunakan di bidang teknik, navigasi, fisika dan geometri.

Definisi trigonometri invers:

Jika x = sin y, maka fungsi invers dari sinus didefinisikan

dengan y = arc sin x.
Dengan cara yang sama, jika:
x = cos y maka inversnya adalah y = arc sin x;
x = ta
n y maka inversnya adalah y = arc tan x.

Rumus integrasi fungsi arcsinus

{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)+{\sqrt {1-x^{2}}}+C}
{\displaystyle \int \arcsin(a\,x)\,dx=x\arcsin(a\,x)+{\frac {\sqrt {1-a^{2}\,x^{2}}}{a}}+C}
{\displaystyle \int x\arcsin(a\,x)\,dx={\frac {x^{2}\arcsin(a\,x)}{2}}-{\frac {\arcsin(a\,x)}{4\,a^{2}}}+{\frac {x{\sqrt {1-a^{2}\,x^{2}}}}{4\,a}}+C}
{\displaystyle \int x^{2}\arcsin(a\,x)\,dx={\frac {x^{3}\arcsin(a\,x)}{3}}+{\frac {\left(a^{2}\,x^{2}+2\right){\sqrt {1-a^{2}\,x^{2}}}}{9\,a^{3}}}+C}
{\displaystyle \int x^{m}\arcsin(a\,x)\,dx={\frac {x^{m+1}\arcsin(a\,x)}{m+1}}\,-\,{\frac {a}{m+1}}\int {\frac {x^{m+1}}{\sqrt {1-a^{2}\,x^{2}}}}\,dx\quad (m\neq -1)}
{\displaystyle \int \arcsin(a\,x)^{2}\,dx=-2\,x+x\arcsin(a\,x)^{2}+{\frac {2{\sqrt {1-a^{2}\,x^{2}}}\arcsin(a\,x)}{a}}+C}
{\displaystyle \int \arcsin(a\,x)^{n}\,dx=x\arcsin(a\,x)^{n}\,+\,{\frac {n{\sqrt {1-a^{2}\,x^{2}}}\arcsin(a\,x)^{n-1}}{a}}\,-\,n\,(n-1)\int \arcsin(a\,x)^{n-2}\,dx}
{\displaystyle \int \arcsin(a\,x)^{n}\,dx={\frac {x\arcsin(a\,x)^{n+2}}{(n+1)\,(n+2)}}\,+\,{\frac {{\sqrt {1-a^{2}\,x^{2}}}\arcsin(a\,x)^{n+1}}{a\,(n+1)}}\,-\,{\frac {1}{(n+1)\,(n+2)}}\int \arcsin(a\,x)^{n+2}\,dx\quad (n\neq -1,-2)}

Rumus integrasi fungsi arckosinus

{\displaystyle \int \arccos(x)\,dx=x\arccos(x)-{\sqrt {1-x^{2}}}+C}
{\displaystyle \int \arccos(a\,x)\,dx=x\arccos(a\,x)-{\frac {\sqrt {1-a^{2}\,x^{2}}}{a}}+C}
{\displaystyle \int x\arccos(a\,x)\,dx={\frac {x^{2}\arccos(a\,x)}{2}}-{\frac {\arccos(a\,x)}{4\,a^{2}}}-{\frac {x{\sqrt {1-a^{2}\,x^{2}}}}{4\,a}}+C}
{\displaystyle \int x^{2}\arccos(a\,x)\,dx={\frac {x^{3}\arccos(a\,x)}{3}}-{\frac {\left(a^{2}\,x^{2}+2\right){\sqrt {1-a^{2}\,x^{2}}}}{9\,a^{3}}}+C}
{\displaystyle \int x^{m}\arccos(a\,x)\,dx={\frac {x^{m+1}\arccos(a\,x)}{m+1}}\,+\,{\frac {a}{m+1}}\int {\frac {x^{m+1}}{\sqrt {1-a^{2}\,x^{2}}}}\,dx\quad (m\neq -1)}
{\displaystyle \int \arccos(a\,x)^{2}\,dx=-2\,x+x\arccos(a\,x)^{2}-{\frac {2{\sqrt {1-a^{2}\,x^{2}}}\arccos(a\,x)}{a}}+C}
{\displaystyle \int \arccos(a\,x)^{n}\,dx=x\arccos(a\,x)^{n}\,-\,{\frac {n{\sqrt {1-a^{2}\,x^{2}}}\arccos(a\,x)^{n-1}}{a}}\,-\,n\,(n-1)\int \arccos(a\,x)^{n-2}\,dx}
{\displaystyle \int \arccos(a\,x)^{n}\,dx={\frac {x\arccos(a\,x)^{n+2}}{(n+1)\,(n+2)}}\,-\,{\frac {{\sqrt {1-a^{2}\,x^{2}}}\arccos(a\,x)^{n+1}}{a\,(n+1)}}\,-\,{\frac {1}{(n+1)\,(n+2)}}\int \arccos(a\,x)^{n+2}\,dx\quad (n\neq -1,-2)}

Rumus integrasi fungsi arctangen

{\displaystyle \int \arctan(x)\,dx=x\arctan(x)-{\frac {\ln \left(x^{2}+1\right)}{2}}+C}
{\displaystyle \int \arctan(a\,x)\,dx=x\arctan(a\,x)-{\frac {\ln \left(a^{2}\,x^{2}+1\right)}{2\,a}}+C}
{\displaystyle \int x\arctan(a\,x)\,dx={\frac {x^{2}\arctan(a\,x)}{2}}+{\frac {\arctan(a\,x)}{2\,a^{2}}}-{\frac {x}{2\,a}}+C}
{\displaystyle \int x^{2}\arctan(a\,x)\,dx={\frac {x^{3}\arctan(a\,x)}{3}}+{\frac {\ln \left(a^{2}\,x^{2}+1\right)}{6\,a^{3}}}-{\frac {x^{2}}{6\,a}}+C}
{\displaystyle \int x^{m}\arctan(a\,x)\,dx={\frac {x^{m+1}\arctan(a\,x)}{m+1}}-{\frac {a}{m+1}}\int {\frac {x^{m+1}}{a^{2}\,x^{2}+1}}\,dx\quad (m\neq -1)}

Rumus integrasi fungsi arckotangen

{\displaystyle \int \operatorname {arccot}(x)\,dx=x\operatorname {arccot}(x)+{\frac {\ln \left(x^{2}+1\right)}{2}}+C}
{\displaystyle \int \operatorname {arccot}(a\,x)\,dx=x\operatorname {arccot}(a\,x)+{\frac {\ln \left(a^{2}\,x^{2}+1\right)}{2\,a}}+C}
{\displaystyle \int x\operatorname {arccot}(a\,x)\,dx={\frac {x^{2}\operatorname {arccot}(a\,x)}{2}}+{\frac {\operatorname {arccot}(a\,x)}{2\,a^{2}}}+{\frac {x}{2\,a}}+C}
{\displaystyle \int x^{2}\operatorname {arccot}(a\,x)\,dx={\frac {x^{3}\operatorname {arccot}(a\,x)}{3}}-{\frac {\ln \left(a^{2}\,x^{2}+1\right)}{6\,a^{3}}}+{\frac {x^{2}}{6\,a}}+C}
{\displaystyle \int x^{m}\operatorname {arccot}(a\,x)\,dx={\frac {x^{m+1}\operatorname {arccot}(a\,x)}{m+1}}+{\frac {a}{m+1}}\int {\frac {x^{m+1}}{a^{2}\,x^{2}+1}}\,dx\quad (m\neq -1)}

Rumus integrasi fungsi arcsekan

{\displaystyle \int \operatorname {arcsec}(x)\,dx=x\operatorname {arcsec}(x)-\operatorname {arctan} \,{\sqrt {1-{\frac {1}{x^{2}}}}}+C}
{\displaystyle \int \operatorname {arcsec}(a\,x)\,dx=x\operatorname {arcsec}(a\,x)-{\frac {1}{a}}\,\operatorname {arctanh} \,{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}+C}
{\displaystyle \int x\operatorname {arcsec}(a\,x)\,dx={\frac {x^{2}\operatorname {arcsec}(a\,x)}{2}}-{\frac {x}{2\,a}}{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}+C}
{\displaystyle \int x^{2}\operatorname {arcsec}(a\,x)\,dx={\frac {x^{3}\operatorname {arcsec}(a\,x)}{3}}\,-\,{\frac {1}{6\,a^{3}}}\,\operatorname {arctanh} \,{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}\,-\,{\frac {x^{2}}{6\,a}}{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}\,+\,C}
{\displaystyle \int x^{m}\operatorname {arcsec}(a\,x)\,dx={\frac {x^{m+1}\operatorname {arcsec}(a\,x)}{m+1}}\,-\,{\frac {1}{a\,(m+1)}}\int {\frac {x^{m-1}}{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}}\,dx\quad (m\neq -1)}

Rumus integrasi fungsi arckosekan

{\displaystyle \int \operatorname {arccsc}(x)\,dx=x\operatorname {arccsc}(x)\,+\,\ln \left|x+{\sqrt {x^{2}-1}}\right|\,+\,C=x\operatorname {arccsc}(x)\,+\,\operatorname {arccosh} (x)\,+\,C}
{\displaystyle \int \operatorname {arccsc}(a\,x)\,dx=x\operatorname {arccsc}(a\,x)+{\frac {1}{a}}\,\operatorname {arctanh} \,{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}+C}
{\displaystyle \int x\operatorname {arccsc}(a\,x)\,dx={\frac {x^{2}\operatorname {arccsc}(a\,x)}{2}}+{\frac {x}{2\,a}}{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}+C}
{\displaystyle \int x^{2}\operatorname {arccsc}(a\,x)\,dx={\frac {x^{3}\operatorname {arccsc}(a\,x)}{3}}\,+\,{\frac {1}{6\,a^{3}}}\,\operatorname {arctanh} \,{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}\,+\,{\frac {x^{2}}{6\,a}}{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}\,+\,C}
{\displaystyle \int x^{m}\operatorname {arccsc}(a\,x)\,dx={\frac {x^{m+1}\operatorname {arccsc}(a\,x)}{m+1}}\,+\,{\frac {1}{a\,(m+1)}}\int {\frac {x^{m-1}}{\sqrt {1-{\frac {1}{a^{2}\,x^{2}}}}}}\,dx\quad (m\neq -1)}

Daftar Integral 

Daftar integral (antiderivatif) dari ekspresi yang melibatkan fungsi invers trigonometri.

  • Fungsi invers (= “fungsi kebalikan”) trigonometri juga dikenal sebagai “fungsi arc” (“arc functions“).
  • C digunakan untuk melambangkan konstanta integrasi arbitrari yang hanya dapat ditentukan jika nilai integral pada satu titik tertentu telah diketahui. Jadi setiap fungsi mempunyai antiderivatif yang tak terhingga banyaknya.
  • Ada tiga notasi umum untuk fungsi-fungsi invers trigonometri. Fungsi arcsinus, misalnya, dapat ditulis sebagai sin−1, asin, atau, pada halaman ini , arcsin.
  • Untuk setiap rumus integrasi fungsi invers trigonometri di bawah ini ada rumus yang bersangkutan dalam daftar integral dari fungsi invers hiperbolik.
NamaNotasiDefinisiDomain x untuk bilangan riilRange
(radian)		Range
(derajat)
arcsinusy = arcsin(x)x = sin(y)−1 ≤ x ≤ 1−π2 ≤ y ≤ π2−90° ≤ y ≤ 90°
arckosinusy = arccos(x)x = cos(y)−1 ≤ x ≤ 10 ≤ y ≤ π0° ≤ y ≤ 180°
arctangeny = arctan(x)x = tan(y)semua bilangan riil−π2 < y < π2−90° < y < 90°
arckotangeny = arccot(x)x = cot(y)semua bilangan riil0 < y < π0° < y < 180°
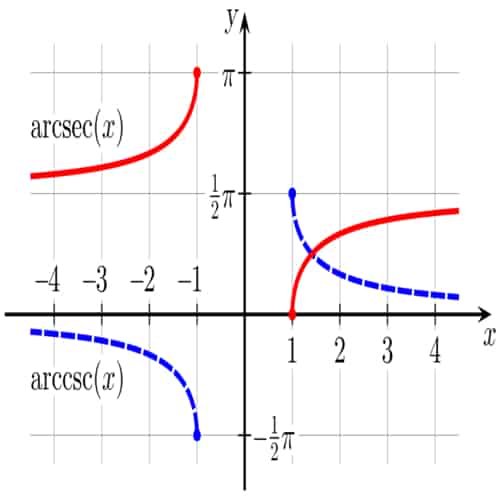
arcsekany = arcsec(x)x = sec(y)x ≤ −1 atau 1 ≤ x0 ≤ y < π2 atau π2 < y ≤ π0° ≤ y < 90° atau 90° < y ≤ 180°
arccosekany = arccsc(x)x = csc(y)x ≤ −1 atau 1 ≤ x−π2 ≤ y < 0 atau 0 < y ≤ π2−90° ≤ y < 0° atau 0° < y ≤ 90°

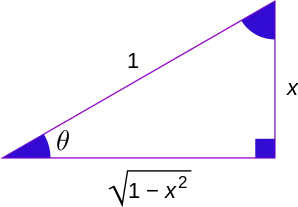
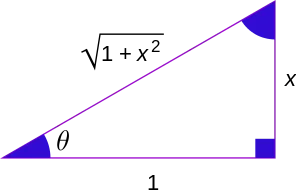
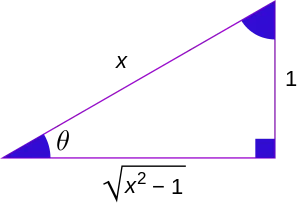
Hubungan antara fungsi trigonometri dengan fungsi trigonometri invers

{\displaystyle \theta } theta{\displaystyle \sin(\theta )} sin theta{\displaystyle \cos(\theta )} cos theta{\displaystyle \tan(\theta )} tan thetaDiagram
{\displaystyle \arcsin(x)}{\displaystyle \sin(\arcsin(x))=x}{\displaystyle \cos(\arcsin(x))={\sqrt {1-x^{2}}}}{\displaystyle \tan(\arcsin(x))={\frac {x}{\sqrt {1-x^{2}}}}}Fungsi trigonometri arcsin
{\displaystyle \arccos(x)}{\displaystyle \sin(\arccos(x))={\sqrt {1-x^{2}}}}{\displaystyle \cos(\arccos(x))=x}{\displaystyle \tan(\arccos(x))={\frac {\sqrt {1-x^{2}}}{x}}}Fungsi trigonometri arcos
{\displaystyle \arctan(x)}{\displaystyle \sin(\arctan(x))={\frac {x}{\sqrt {1+x^{2}}}}}{\displaystyle \cos(\arctan(x))={\frac {1}{\sqrt {1+x^{2}}}}}{\displaystyle \tan(\arctan(x))=x}Fungsi trigonometri arctan
{\displaystyle \operatorname {arccsc}(x)}{\displaystyle \sin(\operatorname {arccsc}(x))={\frac {1}{x}}}{\displaystyle \cos(\operatorname {arccsc}(x))={\frac {\sqrt {x^{2}-1}}{x}}}{\displaystyle \tan(\operatorname {arccsc}(x))={\frac {1}{\sqrt {x^{2}-1}}}}Fungsi trigonometri arccsc
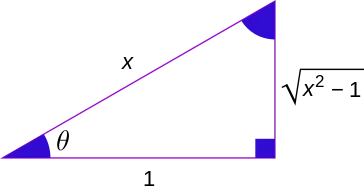{\displaystyle \operatorname {arcsec}(x)}{\displaystyle \sin(\operatorname {arcsec}(x))={\frac {\sqrt {x^{2}-1}}{x}}}{\displaystyle \cos(\operatorname {arcsec}(x))={\frac {1}{x}}}{\displaystyle \tan(\operatorname {arcsec}(x))={\sqrt {x^{2}-1}}}Fungsi trigonometri arcsec
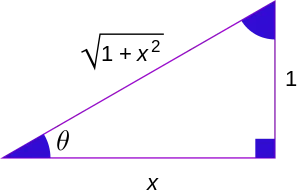{\displaystyle \operatorname {arccot}(x)}{\displaystyle \sin(\operatorname {arccot}(x))={\frac {1}{\sqrt {1+x^{2}}}}}{\displaystyle \cos(\operatorname {arccot}(x))={\frac {x}{\sqrt {1+x^{2}}}}}{\displaystyle \tan(\operatorname {arccot}(x))={\frac {1}{x}}}Fungsi trigonometri arccot
Trigonometri invers arctangent arccotangent
Nilai-nilai utama yang biasa dari arctan (x) dan arccot (x) fungsi digambarkan pada bidang kartesius.
Fungsi trigonometri invers arcsecant arccosecant
Nilai pokok dari fungsi arcsec (x) dan arccsc (x) digambarkan pada bidang kartesian.

Contoh soal dan jawaban Trigonometri Invers

Jika cos y = 0,7071, hitunglah y jika y <90°
Penyelesaian:
cos y = 0,7071
y = arc cos 0,7071
y = 45°
Catatan: ingat bahwa cos 45°
= 0,7071

Jika sin y = 0,5, hitunglah y, jika y < 90°

Penyelesaian:
sin y = 0,5
y = arc sin 0,5
y = 30°
Catatan: ingat bahwa sin 30°
= 0,5

Jika tan y = 1,7321, hitunglah y, jika y < 90°

Penyelesaian:
tan y = 1,7321
y = arc tan 1,7321
y = 60°
Catatan: ingat bahwa tan 60°
= 1,7321

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math Only Math, Wolfram

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

Pinter Pandai
«
»

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

PinterPandai
Okt 14, 2024 58 sec read

Tes matematika logika: Jika 4 + 3 = 27,…

PinterPandai
Okt 9, 2024 1 min read

Nilai Pi 1 juta digit pertama | Analisis dan…

PinterPandai
Mei 8, 2024 1 min read

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *