Trapesium

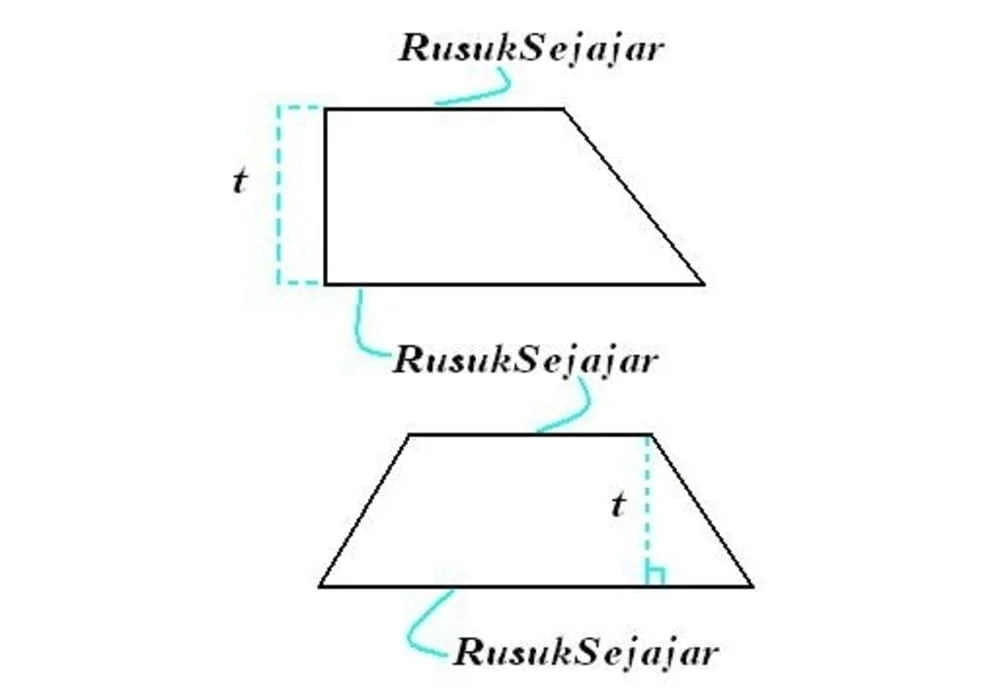
Trapesium adalah bangun datar 2 dimensi yang dibentuk oleh 4 buah rusuk yang dua di antaranya saling sejajar namun tidak sama panjang. Temukan dibawah ini rumus trapesium beserta contoh-contoh soal dan jawabannya.

Trapesium termasuk jenis bangun datar segi empat. Trapesium yang rusuk ketiganya tegak lurus terhadap rusuk-rusuk sejajar disebut trapesium siku-siku.

Rumus trapesium — Trapesium siku-siku dan trapesium biasa dengan tinggi t

Jenis-jenis trapesium dalam rumus geometri

Trapesium terdiri dari 3 jenis, yaitu:

Trapesium sembarang, yaitu trapesium yang keempat rusuknya tidak sama panjang. Trapesium ini tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
Trapesium sama kaki, yaitu trapesium yang mempunyai sepasang rusuk yang sama panjang, di samping mempunyai sepasang rusuk yang sejajar. Trapesium ini memiliki 1 simetri lipat dan 1 simetri putar.
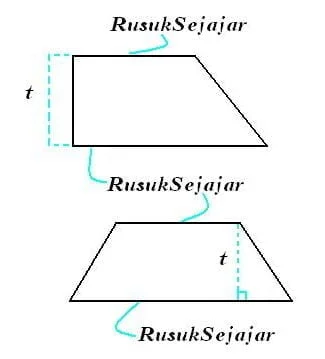
Trapesium siku-siku, yaitu trapesium yang mana dua di antara keempat sudutnya merupakan sudut siku-siku. Rusuk-rusuk yang sejajar tegak lurus dengan tinggi trapesium ini. Trapesium ini tidak memiliki simetri lipat dan hanya memiliki satu simetri putar.

Contoh Trapesium Sembarang ABCD

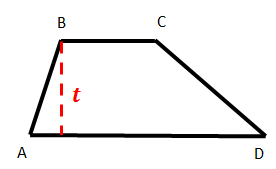
Trapesium sembarang adalah trapesium dengan keempat rusuk/sisinya tidak sama panjang. Trapesium sembarang tidak memiliki simetri lipat.Luas Trapesium Sembarang _ABCD = (BC + AD) x t / 2

Keliling Trapesium_ABCD= AB + BC + CD + DA

Contoh Trapesium Siku-siku PQRS

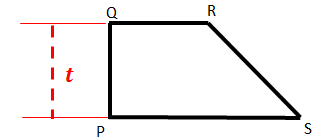
Trapesium siku-siku adalah trapesium yang memiliki dua sudut siku-siku dan rusuk / sisi yang saling sejajar tegak lurus dengan rusuk tinggi trapesium. Trapesium siku-siku juga tidak memiliki simetri lipat.Luas Trapesium Siku-siku _PQRS = (QR + PS) x t / 2

Keliling Trapesium PQRS = PQ + QR + RS + SP

Contoh Trapesium Samakaki KLMN

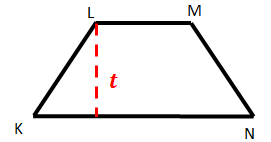
Trapesium samakaki adalah trapesium yang memiliki rusuk yang sama panjang dan rusuk sejajar. Trapesium samakaki memiliki 1 simetri lipat.Luas Trapesium Sama kaki_KLMN = (LM + KN) x t / 2

Keliling Trapesium KLMN = KL + LM + MN + NP

Rumus trapesium

Keliling

K=AB+BC+CD+DA

Luas

{\textstyle L={\frac {{\text{Jumlah rusuk sejajar}}\times {\text{tinggi}}}{2}}\ }

Volume

V = Luas alas trapesium x tinggi prisma

= (½ (Jumlah sisi sejajar x tinggi trapesium)) x tinggi prisma

Soal dan Jawaban Trapesium

Dibawah ini adalah gambar trapesium siku-siku yang merupakan alas dari sebuah prisma. Jika tinggi prisma 15 cm,maka luas seluruh permukaan prisma adalah … cm².

Jawaban:
t trapesium=√13² − 5²
= √169 − 25
= √144
= 12
L=2⋅L alas+K alas⋅t
= 2 (1/2 x (12+7) x 12) + (12+13+7+12)15
= (19×12) + (44×15)
= 228 + 660
= 888

Sebuah trapesium memiliki sisi sejajar 6 cm dan 14 cm serta tinggi 4 cm. Berapakah luas trapesium tersebut?

Jawaban:
Rumus trapesium untuk mencari luas: ${\textstyle L={\frac {{\text{Jumlah rusuk sejajar}}\times {\text{tinggi}}}{2}}\ }$

Luas trapesium = jumlah sisi sejajar x tinggi / 2 = (6+14) x 4 / 2 = 40 cm².

Jika panjang kedua sisi miring pada trapesium pada soal 1 adalah 5 cm, berapakah keliling trapesium?

Jawaban:
Keliling trapesium = panjang semua rusuk = 6 + 14 + 5 + 5 = 30cm.

Sebuah trapesium sama kaki ABCD memiliki panjang sisi-sisi sejajar berturut-turut 8cm dan 12cm, serta sisi tegak trapesium (kaki trapesium) 5cm. Hitunglah keliling trapesium ABCD tersebut!

Jawaban:

Panjang AB = 12 cm
Panjang BC = DA = 5 cm
Panjang CD = 8 cm

Gunakan rumus trapesium untuk mencari keliling trapesium = AB+BC+CD+DA

= 12 + 5 + 8 + 5
= 30 cm

Sebuah trapesium CDEF memiliki panjang sisi-sisi sejajar berturut-turut 5 cm dan 9 cm serta tinggi 6 cm. Maka, berapakah luas trapesium tersebut?

Jawaban:
Gunakan rumus trapesium untuk mencari luas trapesium: ${\textstyle L={\frac {{\text{Jumlah rusuk sejajar}}\times {\text{tinggi}}}{2}}\ }$

Luas = ½ x (CD + EF) x t
Luas = ½ x (5 cm + 9 cm) x 6 cm
Luas = ½ x 14 x 6
Luas = ½ x 84 cm
Luas = 42 cm

Diketahui sebuah prisma trapesium memiliki alas berbentuk trapesium dengan panjang sisi berturut-turut yaitu 5cm dan 7 cm, serta tinggi trapesium 4 cm. Sedangkan tinggi prisma adalah 8 cm. Hitunglah volume dari prisma trapesium tersebut!

Jawaban:

Luas alas trapesium = ½ x (AB + CD) x t

= ½ x (7 cm + 5cm) x 4 cm
= ½ x 12 x 4
= ½ x 48 cm
= 24 cm

Tinggi prisma = 8 cm

Jadi, Volume prisma = luas alas x tinggi prisma

= 24 x 8
= 192 cm³

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Tetrahedron geometri adalah bentuk geometrik 3 dimensi. Ini adalah polihedron terkecil. Hal ini terdiri 4 wajah segitiga, 3 dari yang bergabung di setiap sudut. Angka ini digunakan secara luas dalam arsitektur dan seni modern. Tetrahedron juga digunakan untuk memecahkan masalah geometris yang rumit. Klik disini untuk mengetahui lebih lanjut (akan membuka layar baru).

Bacaan Lainnya

Sumber bacaan: Math Warehouse, Math Open Reference

Rumus Trapesium Berserta Contoh Soal dan Jawaban