Tabung (rumus geometri)

Dalam geometri, tabung atau silinder adalah bangun ruang 3 dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki 3 sisi dan 2 rusuk. Temukan rumus tabung dibawah ini.

Kedua lingkaran disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung.

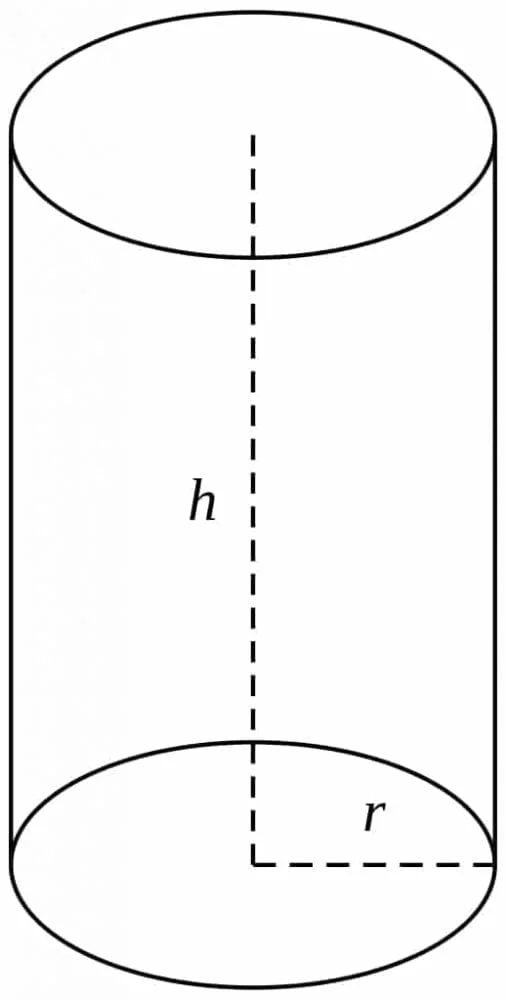
Rumus Tabung (Silinder)

r=r_{\text{alas}}

t=h/_{\text{tinggi}}

d=d_{\text{alas}}

Luas alas tabung

L=\pi r^{2}

Luas selimut tabung

L=2\pi rt

Luas permukaan tabung

L=\ L_{\text{alas}}+L_{\text{selimut}}

=\pi d(r+t)

=2\cdot \pi r^{2}+2\pi r\cdot t\,

, atau

=2\cdot \pi r\cdot (r+t)

Luas permukaan tanpa tutup tabung

L=\ L_{\text{alas}}+L_{\text{selimut}}

=\pi r^{2}+2\pi r\cdot t

=\pi r(r+2\cdot t)

Rumus keliling Alas tabung

Keliling alas = 2πr

Rumus volume tabung

V=\pi r^{2}\cdot t

={\frac {1}{4}}\pi d^{2}\cdot t

Soal dan Jawaban Rumus Tabung

Gunakan rumus tabung diatas untuk menyelesaikan soal-soal dibawah ini.

1. Sebuah tabung memiliki jari-jari berukuran 10 cm. Jika tingginya 21 cm, tentukanlah volume tabung tersebut!

Penyelesaian:
Diketahui: Jari-jari (r) = 10 cm

Tinggi (t ) = 21 cm

Ditanya: Volume tabung (v)

Jawaban:
Jadi volume tabung tersebut adalah 6600 cm³

2. Sekeping koin logam memiliki tebal 1,4 mm dan diameter 20 mm. Berapa volume koin tersebut? (Petunjuk rumus tabung: volume silinder = pi x radius x radius x tinggi).

Jawaban:
Tebal koin = tinggi silinder yaitu 1,4 mm.
Radius koin = setengah kali diameter yaitu 10 mm.
Volume koin = (22/7) x 10 mm x 10 mm x 1,4 mm = 440 mm3.

3. Sebongkah es batu dicetak membentuk silinder dengan ukuran jari-jari silinder dan tebalnya sama yaitu 35 cm. Berapa volume silinder es tersebut? (Petunjuk rumus tabung: volume silinder = pi x radius x radius x tinggi).

Jawaban:
Radius = jari-jari silinder yaitu 35 cm.
Tinggi silinder = tebal silinder = 35 cm.
Volume silinder es = (22/7) x 35 cm x 35 cm x 35 cm = 134.750 cm3.

4. John memiliki tangki minyak berbentuk tabung dengan tinggi 2 meter. Jika diisi minyak hingga penuh, tangki tersebut dapat menampung 2260,8 liter minyak. Berapa volume tangki minyak milik John?

Penyelesaian:
Diketahui : Volume (v) = 2260,8 liter =2.260.800 cm³

Tinggi (t ) = 2 m = 200 cm

Ditanya : jari-jari (r)

Jawaban:
Jadi jari-jari tangki tersebut adalah 60cm.

5. Sebatang besi sepanjang 7 meter mempunyai penampang berbentuk lingkaran dengan diameter 1 cm. Berapa volume batang besi tersebut dalam centimeter kubik? (Petunjuk: volume silinder = pi x radius x radius x tinggi).

Jawaban:
Panjang besi = tinggi silinder yaitu 7 m = 700 cm.
Radius silinder = setengah kali diameter batang besi yaitu 0,5 cm.
Volume batang besi = (22/7) x 0,5 cm x 0,5 cm x 700 cm = 550 cm3.

6. Sebuah drum (tabung) memiliki diameter 30cm dan tinggi 90cm, berapakah volume drum tersebut? (Petunjuk rumus tabung: Volume drum = π x r x r x t.

Jawaban: 3,14 x 15 x 15 x 90 = 63.585 cm³

7. Sebatang pipa berbentuk tabung memiliki panjang 14 meter dan berjari-jari 3 cm. Berapa liter volume pipa tersebut?

Penyelesaian:
Diketahui: jari-jari (r) = 3 cm

Tinggi (t ) = 14 m = 1400 cm

Ditanya: Volume tabung (v)

Jawaban:
Volume pipa tersebut adalah 39,6 liter

8. Besi dengan panjang 2 meter, memiliki diameter 3 cm, berapakah volumenya?

Rumus sama dengan di atas

Kita harus merubah dari Meter ke Centi meter ya, jadi 2 m = 200 cm

Jawaban: 3,14 x 1,5 x 1,5 x 200 = 1.413 cm³

9. Berapa volume sebuah tabung yang memiliki diameter 20 cm dan tinggi 28 cm? (Petunjuk: volume silinder = pi x radius x radius x tinggi).

Jawaban:
Radius silinder adalah setengah dari diameter yaitu 10 cm.
Volume tabung = (22/7) x 10 cm x 10 cm x 28 cm = 8.800 cm3.

10. Apabila ada sebuah tabung yang diketahui memiliki jari – jari yaitu 16 cm. Carilah dan hitinglah keliling alas tabung tersebut:

Penyelesaian:

Diketahui:
r = 16 cm

Yang ditanya : K = …?

Jawab :

K = 2 x π x r
K = 2 x 22/7 x 16
K = 704 / 7
K = 100.57 cm

Maka, keliling alas tabung tersebut ialah = 100.57 cm

11. Sebuah drum berbentuk tabung memiliki volume 88.704 cm³. Jika tingginya 36 cm, tentuknlah ukuran jari-jari tabung tersebut!

Penyelesaian:
Diketahui: volume (v) = 88.704 cm³

Tinggi (t ) = 36 cm

Ditanya : jari-jari (r)

Jawaban:
Jadi jari-jari tangki tersebut adalah 28 cm.

12. Sepotong kayu dibentuk menjadi sebuah silinder dengan luas penampang 240 cm2. Silinder kayu tersebut tingginya 50 cm. Berapa volume silinder kayu tersebut? (Petunjuk: volume silinder = luas penampang lingkaran x tinggi).

Jawaban:
Volume silinder kayu = 240 cm2 x 50 cm = 12.000 cm3.

13. Sebanyak 165 liter bensin ditungkan ke dalam drum berbentuk tabung dengan jari-jari 30 cm. Berapakah ketinggian bensin dalam drum tersebut?

Penyelesaian:
Diketahui: volume (v) = 165 liter = 165.000 cm³

Jari-jari (r ) = 30 cm

Ditanya: tinggi (t)

Jawaban:
Jadi ketinggian bensin dalam drum adalah 58,38 cm³

14. Ke dalam tabung berisi air setinggi 30 cm dimasukkan 6 bola besi yang masing-masing berjari-jari 7 cm. Jika diameter tabung 28 cm, tinggi air dalam tabung setelah dimasukkan enam bola besi adalah…

Pembahasan:
Mencari volume air dalam tabung sebelum dimasuki bola besi:

$V_{air} = \pi r^{2}t$

$V_{air} = \frac{22}{7} \times 14^{2} \times 30$

$V_{air} = \frac{22}{7} \times 196 \times 30$

$V_{air} = \frac{22}{7} \times 5.880$

$V_{air} = 18.480 \; cm^{3}$

Mencari volume 6 bola besi yang dimasukkan ke dalam tabung:

$V_{6 \; bola \; besi} = 6 \times \frac{4}{3} \pi r^{3}$

$V_{6 \; bola \; besi} = 6 \times \frac{4}{3} \times \frac{22}{7} \times 7^{3}$

$V_{6 \; bola \; besi} = 6 \times \frac{4}{3} \times 1.078$

$V_{6 \; bola \; besi} = 8.624 \; cm^{3}$

Volume gabungan air dan bola besi:

$= 18.480 + 8.624$

$= 27.104 \; cm^{3}$

Mencari tinggi air setelah bola besi dimasukkan dalam tabung:

$V = 27.104$

$\pi r^{2} t = 27.104$

$\frac{22}{7} \times 14^{2} \times t_{air} = 27.104$

$\frac{22}{7} \times 196 \times t_{air} = 27.104$

$616 t_{air} = 27.104$

$t_{air} = \frac{27.104}{616}$

$t_{air} = 44 \; cm$

Jawaban: 44 cm

15. Jari-jari sebuah tabung 7 cm. Jika tinggi tabung 20 cm dan π = 22/7, maka luas alas tabung adalah … cm²

Gunakan rumus tabung: Luas alas $L=\pi r^{2}$

= 22/7 x 7 = 154 cm²

16. Sebuah tabung mempunyai diameter dan tinggi yang masing masing ukuranya ialah 16 dan 12. Berapakah Luas permukaan yang dimiliki tabung tersebut?

Jawab : 2 × phi × r (r+t)
2 × 22/7 × 8 (8 + 12)
44 (17) = 160

Luas selimut Tabung, rumusnya: 2 × phi × r × t
Contoh soalnya : Apabiladiketahui sebuah tabung yang memiliki r = 14 dan tinggi 30. Tentukanlah luas selimut tabung tersebut:
Jawab :

Rumus: 2 × phi × r × t
2 × 22/7 × 14 × 30
44 × 50 = 2540

17. Diketahui luas alas tabung 154 cm². Jika volume tabung 3080 cm³ dan π = 22/7, maka luas selimut tabung adalah … cm²

Jawaban:
πr² = 154
22/7 x r² = 154
r² = 7 x 7
r = 7

154 x t = 3080
t = 3080 : 154
t = 20

Luas selimut: 2 πrt
= 2 x 22/7 x 7 x 20
= 880

18. Diketahui sebuah tabung berisi air berjari-jari 14 cm dan tinggi tabung 30 cm. Jika keliling air 10cm dan kedalam tabung tersebut dimasukan balok berukuran 22 cm×14 cm×6 cm, maka ketinggian air setelah dimasukan balok menjadi … cm.

Jawaban:
Volulme air yang naik=Volume balok

πr2t = 22 × 14 × 6
22/7 × 14 × 14 × t = 22 × 14 × 6
1/7 × 14 × t = 6
⇒ t = 6 : 2 = 3
Ketinggian air menjadi 10 + 3 = 13 cm.

19. Sebuah tabung memiliki jari – jari dan tinggi masing – masing 10 cm dan 30 cm, lalu tentukan lah berapa volume dari tabung tersebut?

Jawaban:

Di ketahui :
r =10 cm
t =30 cmdi tanya :

volume dari tabung tersebut?volume = π x r² x t
=3,14 x 10 cm x 10 cm x 30 cm
= 942 cm³Jadi, volume dari tabung tersebut adalah 942 cm³

20. Diketahui luas lingkaran=25 π cm² dan tinggi tabung 12 cm. Luas selimut tabung = … cm².

Jawaban:
πr = 25 π ⇒ r² = 25 ⇒ r = 5
L selimut = 2 πrt = 2π × 5 × 12 = 120π

21. Sebuah tabung memiliki jari – jari 14 cm dan tinggi nya 10 cm, maka tentukan luasnya?

Jawaban:

di ketahui :

r = 14 cm
t = 10 cm

di tanya= luas?

luas =2 x π x r (r+t)

=2 x 22/7 x 14 cm x 10 cm (14 cm + 10 cm)
=2 x 44 cm x 10 cm (24 cm)
=21120 cm²

Jadi, luasnya adalah 21120 cm²

22. Pak Budi memotong sebuah kayu menjadi sebuah tabung atau silinder dengan luas penampang alasanya ialah 350cm². Tabung atau silinder dari kayu tersebut memiliki tinggi 45 cm. Hitunglah volume tabung atau silinder dari kayu tersebut:

Jawab :

Volume silinder = luas penampang alas atau lingkaran x tinggi
Volume silinder kayu = 350 cm² x 45 cm = 15.750 cm³.

Maka, volume silinder tersebut ialah 15.750 cm³.

23. Sebuah drum minyak tanah berbentuk tabung berjari-jari 35cm. Jika tinggi tabung 0,5m, maka volume drum tersebut adalah… liter.

Jawaban:

0,5m = 50cm
Volume drum = πr 2t

=22/7 × 35 × 35 × 50
=110 × 35 × 50
=192.500 cm³
=192,5 liter

24. Sebongkah es batu dicetak dengan bentuk tabung dengan ukuran radius atau jari-jarinya 35 cm dan tingginya 35 cm. Berapakah volume tabung es tersebut?

Jawaban:

Volume tabung = phi x radius x radius x tinggi

Volume tabung = 22/7 x 35×35 x35 = 134.750 cm²

25. Hitunglah volume tabung yang mempunyai diameter 40cm serta tinggi 56cm ?

Jawab :

Diameter = 40 cm, sehingga r = ½ diameter = 20cm

Tinggi = 56cm

Volume tabung = π x r² x t

= 22/7 x 20x20x 56

= 22/7 x 22.400 = 70.400 cm³

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Tetrahedron geometri adalah bentuk geometrik 3 dimensi. Ini adalah polihedron terkecil. Hal ini terdiri 4 wajah segitiga, 3 dari yang bergabung di setiap sudut. Angka ini digunakan secara luas dalam arsitektur dan seni modern. Tetrahedron juga digunakan untuk memecahkan masalah geometris yang rumit. Klik disini untuk mengetahui lebih lanjut (akan membuka layar baru).

Bacaan Lainnya

Rumus Tabung Berserta Contoh Soal dan Jawaban

Tabung (rumus geometri)