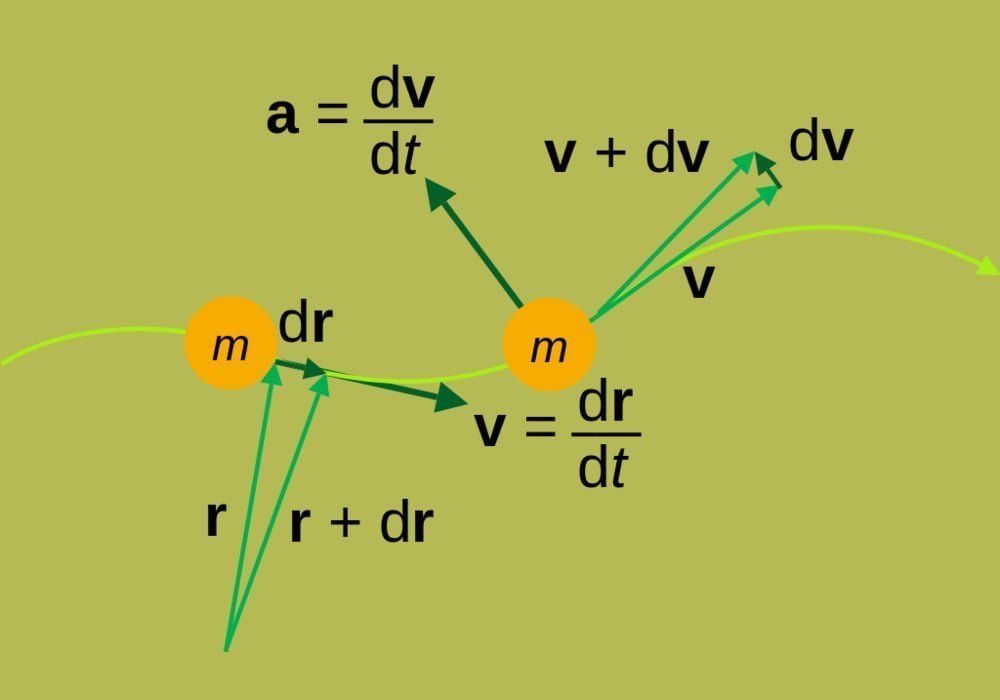
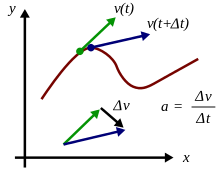
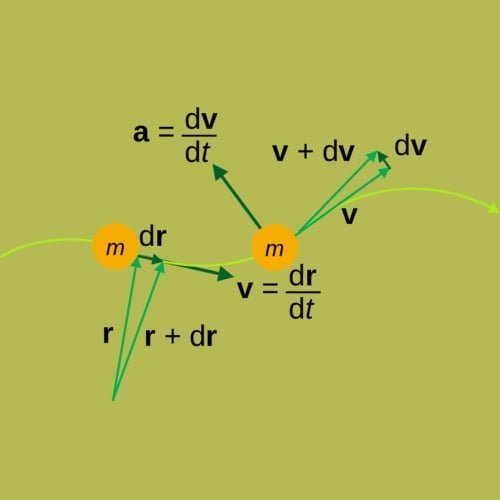
Rumus Percepatan (Akselerasi) Fisika

Rumus Percepatan (Akselerasi)

Percepatan atau akselerasi adalah perubahan kecepatan dalam satuan waktu tertentu. Akselerasi sebuah objek disebabkan karena gaya yang bekerja pada objek tersebut, seperti yang dijelaskan dalam Hukum Kedua Newton. Temukan dibawah ini rumus percepatan.

Satuan SI untuk akselerasi adalah meter per sekon kuadrat (m s⁻²). Percepatan adalah besaran vektor, sehingga percepatan memiliki besaran dan arah.

Sebagai vektor, total gaya sama dengan hasil kali massa objek (besaran skalar) dan percepatannya. Umumnya, percepatan dilihat sebagai gerakan suatu objek yang semakin cepat ataupun lambat. Dengan kata lain, objek yang membelok (misalnya mobil yang sedang menikung)-pun memiliki percepatan juga.

Definisi dan Sifat-Sifat Rumus Percepatan (Akselerasi)

Percepatan kinematis — Besaran kinematis pada partikel klasik: massa m, posisi r, kecepatan v, percepatan a.

Rumus Percepatan rata-rata

Akselerasi adalah perubahan kecepatan. Pada titik manapun pada lintasan, besaran percepatan sama dengan perubahan kecepatan pada besaran dan arah pada titik tersebut. Akselerasi sebenarnya pada waktu tadalah limit sebagai interval waktu Δt→ 0 dari Δv/Δt

Percepatan rata-rata suatu objek untuk tiap waktu adalah perubahan kecepatan $(\Delta \mathbf {v} )$ dibagi waktu $(\Delta t)$ . Secara matematis,

\mathbf {\bar {a}} ={\frac {\Delta \mathbf {v} }{\Delta t}}.

Rumus Percepatan sesaat

Dari bawah ke atas:

Fungsi akselerasi a(t);
Integral dari akselerasi adalah fungsi kecepatan v(t);
Integral dari kecepatan adalah fungsi posisi s(t).

Percepatan sesaat, adalah limit dari percepatan rata-rata per interval waktu yang sangat kecil. Dalam kalculus, percepatan sesaat adalah turunan vektor kecepatan terhadap waktu:

\mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}

(Disini dan dimanapun, jika gerak berada dalam garis lurus, besaran vektor dapat digantikan dengan skalar dalam persamaan.)

Dapat dilihat bahwa integral fungsi akselerasi $a (t)$ adalah fungsi kecepatan $v (t)$ ; dimana luasan di bawah kurva akselerasi vs waktu ( $a$ vs. $t$ ) sama dengan kecepatan.

\mathbf {v} =\int \mathbf {a} \ dt

Karena akselerasi didefinisikan sebagai turunan kecepatan $v$ terhadap waktu $t$ dan kecepatan didefinisikan sebagai turunan posisi $x$ terhadap waktu, maka akselerasi adalah turunan kedua dari $x$ terhadap $t$ :

$\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}$

Dalam mekanika klasik, percepatan suatu objek bermassa tetap berbanding lurus dengan resultan gaya yang bekerja padanya dan berbanding terbalik dengan massanya.

$\mathbf {F} =m\mathbf {a} \quad \to \quad \mathbf {a} =\mathbf {F} /m$

dengan F adalah gaya yang bekerja pada objek, m adalah massa objek, dan a adalah percepatan pusat massa benda. Ketika kecepatan semakin mendekati kecepatan cahaya, efek relativistik menjadi semakin besar.

Percepatan bisa bernilai positif dan negatif. Bila nilai percepatan positif, hal ini menunjukkan bahwa kecepatan benda yang mengalami percepatan positif ini bertambah (dipercepat). Sebaliknya bila negatif, hal ini menunjukkan bahwa kecepatan benda menurun (diperlambat). Contoh percepatan positif adalah: jatuhnya buah dari pohonnya yang dipengaruhi oleh gravitasi. Sedangkan contoh percepatan negatif adalah: proses pengereman mobil.

Cara Meghitung Percepatan Rata-Rata Dari Dua Percepatan

1. Tentukan Persamaan Percepatan Rata-rata

Cara menghitung percepatan rata-rata suatu benda dalam rentang waktu tertentu berdasarkan kecepatannya (laju benda tersebut ke arah tertentu), sebelum dan setelah rentang waktu tersebut. Untuk menghitungnya, harus mengetahui persamaan untuk menghitung percepatan:

Keterangannya:

a = percepatan
Δv = perubahan kecepatan
Δt = waktu yang dibutuhkan untuk mengubah kecepatan benda.

– Satuan percepatan adalah meter per sekon per sekon, atau m/s².

– Percepatan adalah besaran vektor, yang berarti mempunyai besar maupun arah.

Besarnya percepatan adalah jumlah totalnya, sedangkan arahnya ditentukan oleh arah gerakan benda. Jika benda melambat, percepatan akan bernilai negatif.

2. Pahami Variabelnya

Untuk bisa menentukan Δv dan Δt dengan perhitungan lebih lanjut:

dan

Keterangannya:

v_t = menyatakan kecepatan akhir
v = kecepatan awal
t_t = waktu akhir
t= waktu awal

– Karena percepatan mempunyai arah, Anda harus selalu mengurangi kecepatan akhir dengan kecepatan awal. Jika Anda membaliknya, arah percepatan yang Anda peroleh akan salah.

– Kecuali dinyatakan lain dalam soal, waktu awal benda bergerak biasanya 0 sekon.

3. Gunakan Rumus untuk Mencari Percepatan

Tuliskan persamaan Anda beserta semua variabel yang diketahui. Persamaannya adalah:

Kurangi kecepatan akhir dengan kecepatan awal, kemudian bagi hasilnya dengan rentang waktu. Hasilnya adalah percepatan rata-rata benda selama rentang waktu tersebut. Jika kecepatan akhir benda lebih kecil dibandingkan kecepatan awalnya, percepatan akan bernilai negatif, atau berarti benda tersebut melambat.

Contoh Soal dan Jawaban Percepatan

1. Kecepatan suatu mobil balap bertambah secara konstan dari 18,5 m/s menjadi 46,1 m/s dalam waktu 2,47 sekon. Berapakah percepatan rata-ratanya?

Jawab:

Diketahui:

v_t = 46,1 m/s
v = 18,5 m/s
t_t = 2,47 s
t = 0 s

Dijawab

a = (46,1 – 18,5) / 2,47 = 11,17 meter/sekon²

2. Sebuah sepeda motor mula-mula bergerak dari kecepatan 2 m/s menjadi 6 m/s selama 10 detik. Berapakah percepatan sepeda motor tersebut?

Jawab:

Diketahui :

v = 2 m/s
v_t = 6 m/s
t = 10 sekon

Ditanya : a = …?

Jawab :

a = 6 – 2 / 10

a = 4 / 10

a = 0,4 m/s²

3. Sebuah bus berhenti untuk menaikkan penumpang. Setelah penumpang naik, bus tersebut melanjutkan perjalanan ke utara. Setelah berjalan 20 sekon, kecepatan bus menjadi 36 km/jam. Berapakah besar percepatannya?

Penyelesaian

v1 = 0 m/s (bus berhenti)

v2 = 36 km/jam

v2 = 36 (1000/3600) m/s

v2 = 10 m/s

t1 = 0 s

t2 = 20 s

Ditanya = a

a = (v2 – v1)/ (t2 – t1)

a = (10 – 0)/(20 – 0)

a = 0,5 m/s2

jadi percepatan bus tersebut adalah 0,5 m/s2

4. Sebuah bus yang awalnya diam kemudian bergerak 36 km/jam selama 5 sekon. Berapakah percepatan bus?

Jawab:

Diketahui :

v = 0 m/s => mengapa bernilai nol? Karena benda yang diam itu nilai kecepatannya nol.

v_t = 36 km/jam = 10 m/s

t = 5 sekon

ditanya : a = …?

Jawab :

a = 10 – 0 / 5

a = 10 / 5 = 2 m/s²

5. Seorang pengendara sepeda berhenti dari kecepatan 22,4 m/s setelah 2,55 sekon menekan rem. Tentukan perlambatannya!

Jawab:

Diketahui:

v_t = 0 m/s

v = 22,4 m/s

t_t = 2,55 s

t = 0 s

Dijawab

a = (0 – 22,4) / 2,55 = – 8,78 meter/sekon²

6. Seoarang siswa mengendarai sepeda dengan kecepatan 7,2 km/jam. Pada suatu tanjakan, siswa tersebut mengurangi kecepatannya sebesar 0,5 m/s2 selama 2 sekon. Berapakah kecepatan akhir siswa tersebut?

Penyelesaian

v1 = 7,2 km/jam

v1 = 7,2 (1.000/3.600) m/s

v1 = 2 m/s

a = −0,5 m/s2 (tanda negatif menunjukkan perlambatan)

t = 2 s

Ditanya = v2

Dari persamaan percepatan berikut:

a = (v2 – v1)/t

Kita mendapatkan persamaan:

v2 = v1 + at

v2 = 2 + (−0,5 × 2)

v2 = 1 m/s

v2 = 3,6 km/jam

jadi, kecepatan akhirnya adalah 3,6 km/jam.

7. Mobil awalnya bergerak dengan kecepatan 10 m/s kemudian di depannya ada kambing lewat dan akhirnya bergerak dengan kecepatan 2 m/s dalam waktu 4 detik. Berapakah perlambatan mobil itu?

Jawab:

Diketahui :

v = 10 m/s

v_t = 2 m/s

t = 4 sekon

Ditanya : a = …?

Dijawab :

a = 2 – 10 / 4

a = – 8 / 10 = – 0,8 m/s²

Nilai di atas percepatannya negatif. Artinya benda itu mengalami perlambatan. Jadi nilai minus (-) artinya perlambatan.

8. Michael mengendarai sepeda motor dengan kecepatan 72 km/jam kemudian di depannya ada lampu lalu lintas dan berhenti dalam waktu 10 sekon. Berapakah perlambatan yang dialami motor Michael?

Jawab:

Diketahui :

v = 72 km/jam = 20 m/s

v_t = 0 m/s ; mengapa nilainya nol? Karena benda itu berhenti artinya diam. Kalau benda diam mempunyai kecepatannya nol (0).

t = 10 sekon

Ditanya : a = …?

Jawab :

a = 0 – 20 / 10

a = – 20 / 10

a = – 2 m/s²

9. Sebuah mobil balap bergerak dalam lintasan lurus dan dinyatakan dalam persamaan v(t) = 10 – 8t + 6t2, dengan t dalam sekon dan v dalam m/s. Tentukan percepatan mobil balap tersebut pada saat t = 3 s!

Penyelesaian

Persamaan kedudukan v(t) = 10 – 8t + 6t2

Untuk t = 3 → v(3) = 10 – 8(3) + 6(3)2 = 40 m/s

Ambil 3 selang waktu (∆t) yang berbeda, misalkan ∆t1 = 0,1 s; ∆t2 = 0,01 s; ∆t3 = 0,001 s

Untuk ∆t = 0,1 s

t2 = t1 + ∆t

t2 = 3 + 0,1 = 3,1 s

v(3,1) = 10 – 8(3,1) + 6(3,1)2 = 42,86 m/s

arata-rata = (v2 – v1)/ (t2 – t1)

arata-rata = (42,86 – 40)/ (3,1 – 3)

arata-rata = 28,6 m/s2

Untuk ∆t = 0,01 s

t2 = t1 + ∆t

t2 = 3 + 0,01 = 3,01 s

v(3,01) = 10 – 8(3,01) + 6(3,01)2 = 40,2806 m/s

arata-rata = (v2 – v1)/ (t2 – t1)

arata-rata = (40,2806 – 40)/ (3,01 – 3)

arata-rata = 28,06 m/s2

Untuk ∆t = 0,001 s

t2 = t1 + ∆t

t2 = 3 + 0,001 = 3,001 s

v(3,001) = 10 – 8(3,001) + 6(3,001)2 = 40,028006 m/s

arata-rata = (v2 – v1)/ (t2 – t1)

arata-rata = (40,028006 – 40)/ (3,001 – 3)

arata-rata = 28,006 m/s2

Untuk selang waktu dan percepatan rata-rata dimasukkan dalam tabel berikut ini.

∆t (s)	a (m/s2)
0,1	28,6
0,01	28,06
0,001	28,006

Berdasarkan tabel di atas, nampak bahwa untuk nilai ∆t yang makin kecil (mendekati nol), percepatan rata-rata makin mendekati nilai 28 m/s2. Oleh karena itu, dapat disimpulkan bahwa percepatan sesaat pada saat t = 3 s adalah 28 m/s2.

Rumus Fisika Lainnya

Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Physics, Tutor Vista

Rumus Percepatan (Akselerasi) Fisika