Kubus (rumus geometri)

Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Kubus juga disebut bidang enam beraturan, selain itu juga merupakan bentuk khusus dalam prisma segiempat. Berikut adalah rumus kubus:

Rumus Kubus

Bila variabel S adalah panjang rusuk kubus, maka:

Luas permukaan

L=6\cdot S^{2}

Volume

V=\ S^{3}

Diagonal sisi

D_{Ss}=S{\sqrt {2}}

Diagonal sisi seluruhnya

D_{Ss}=12\cdot S{\sqrt {2}}

Diagonal ruang

D_{R}=S{\sqrt {3}}

Diagonal ruang seluruhnya

D_{Rs}=4\cdot S{\sqrt {3}}

Luas bidang diagonal

B_{D}=S^{2}{\sqrt {2}}

Luas bidang diagonal seluruhnya

B_{Ds}=6\cdot S^{2}{\sqrt {2}}

Contoh Soal dan Jawaban Kubus

Petunjuk: hafalkan rumus kubus diatas untuk memudahkan Anda menjawab soal-soal dibawah ini.

1. Sebuah lemari es (kulkas) besar yang memiliki panjang, lebar dan sisinya sama yaitu 2 m, Hitunglah berapa volume lemari es tersebut?

Jawaban:
Lemari dengan ukuran panjang, lebar, dan tinggi yang sama (ketiga sisinya sama) adalah sebuah bangun kubus.
Petunjuk: gunakan rumus kubus untuk mencari volume: $V=\ S^{3}$

Volume lemari = 2 m x 2 m x 2 m = 8 m3.

2. Diketahui sebuah kubus memiliki rusuk sepanjang 12 cm. Tentukan volume kubus tersebut!

Jawaban:
Volume = 12 x 12 x 12 = 1.728 cm³

3. Hitunglah volume balok yang berukuran panjang 29 cm, lebar 12 cm, dan tinggi 8 cm!

Jawaban:
Volume = p × l × t
= 29 cm × 12 cm × 8 cm
= 2.784 cm³.

4. Hitung Volum kubus yang mempunyai rusuk 9 cm !

Jawaban:

Volume = s³
= 9³
= 729 cm³.

5. Hitung volume kubus jika luas salah satu sisinya 9 cm² !

Jawaban:

Luas salah satu sisi = 9
s² = 9
s = 3 cm

Volum = s³
= 3³
= 27 cm³

6. Volume sebuah kubus adalah 125 cm³. Hitung panjang rusuk kubus tersebut!

Jawaban:

Volum = s³

125 = s³

5³ = s³
s = 5 cm

7. Hitunglah luas permukaan kubus dengan panjang setiap rusuknya sebagai berikut:
a. 4 cm
b. 7 cm
c. 10 cm
d. 12 cm

Pembahasan dan jawaban:
Gunakan rumus kubus yang tertera di atas.

a.Untuk Panjang Rusuk 4 cm
Luas Permukaan Kubus = 6 x s²
Luas Permukaan Kubus = 6 x 4² = 96 cm²

b.Untuk Panjang Rusuk 7 cm
Luas Permukaan Kubus = 6 x s²
Luas Permukaan Kubus = 6 x 7² = 294 cm²

c.Untuk Panjang Rusuk 10 cm
Luas Permukaan Kubus = 6 x s²
Luas Permukaan Kubus = 6 x 10² = 600 cm²

d.Untuk Panjang Rusuk 12 cm
Luas Permukaan Kubus = 6 x s²
Luas Permukaan Kubus = 6 x 12² = 864 cm²

8. Hitung Luas permukaan kubus dengan panjang rusuk 7 cm !

Jawaban:
Luas permukaan kubus = 6 x s²
= 6 x 72
= 6 x 49
= 294 cm²

9. Hitung Luas permukaan kubus jika luas salah satu sisinya 10 cm² !

Jawaban:
Luas salah satu sisi = 10
s² = 10
Luas permukaan kubus = 6 x s²
= 6 x 10²
= 6 x 100
= 600 cm²

10. Panjang rusuk suatu kubus adalah 15 cm. Berapakah volume bangun tersebut?

Jawaban:
V = 15 x 15 x 15 = 3.375 cm³

11. Volume sebuah kubus adalah 729 cm³. Berapakah rusuk kubus tersebut?

Jawaban:
V = r³
729 = r³
r³ = 729
r = ∛729
r = 9 cm

12. Sebuah kubus dengan rusuk 20 cm dipotong-potong menjadi kubus kecil dengan volume masing-masing 1.000 cm³. Tentukan jumlah kubus kubus kecil yang dihasilkan!

Jawaban:
Volume kubus besar = 20 x 20 x 20 = 8.000 cm³
Volume kubus kecil = 1.000 cm³

Jumlah kubus kecil = volume kubus besar : volume kubus kecil
Jumlah kubus kecil = 8.000 : 1.000 = 8 buah

13. Sebuah wadah berbentuk kubus dengan volume 343 cm³. Berapakah panjang rusuk wadah tersebut?

Jawaban:
r³ = 343
r = ∛343
r = 7 cm

Jumlah rusuk kubus = 12
Jumlah rusuk yang diperlukan = 7 x 12 = 84 cm

14. Berapakah panjang kawat yang diperlukan untuk membuat kubus dengan volume 512 cm³?

Jawaban:
r³ = 512
r = ∛512
r = 8 cm

15. Tony menuangkan air ke dalam wadah berbentuk kubus dengan rusuk 14 cm. Ternyata air yang dituangkan Andi hanya memenuhi setengah wadah tersebut. Berapa banyak air yang dituangkan Tony?

Jawaban:
Volume air = Volume setengah kubus
Volume air = ½ x r³ = ½ x 14³ = ½ x 2.744 = 1.372 cm³

16. Diketahui panjang rusuk sebuah kubus adalah 16 cm. Jika kubus tersebut dipotong-potong menjadi kubus kecil-kecil dengan panjang rusuk masing-masing 4 cm, berapakah jumlah kubus kecil yang dihasilkan?

Jawaban:
Volume kubus besar = 16 x 16 x 16 = 4.096 cm³
Volume kubus kecil = 4 x 4 x 4 = 64 cm³
Jumlah kubus kecil = 4.096 : 64 = 64 buah

17. Berapa luas diagonal bujursangkar dengan rusuk 10 cm? (diketahui √2 = 1,414)

Jawaban:
Petunjug, gunakan rumus kubus untuk mencari diagonalnya: $B_{D}=S^{2}{\sqrt {2}}$
Luas bidang diagonal = 10 x 10 x √2 = 10 x 10 x 1,414 = 141,4 cm2.

18. Hitunglah luas bidang diagonal sebuah kubus yang mempunyai panjang rusuk 24 cm! (diketahui √2 = 1,414)

Jawaban:
Luas bidang diagonal = 24 x 24 x √2 = 10 x 10 x 1,414 = 814,464 cm2.

19. Jessica mempunyai kertas untuk membungkus kado seluas 1,5 m². Kertas tersebut untuk membungkus kado berbentuk kubus dengan ukuran panjang rusuk 45 cm, sisa kertas terluas adalah…. cm²

Jawaban:
Luas permukaan kubus
= 6 × s²
= 6 × 45 × 45
= 12.150 cm²

1,5 m² = 15.000 cm² – 12.150 cm²
= 2.850 cm²

20. Luas permukaan kubus adalah 1.014 $c m^{2}$ . Panjang rusuk kubus adalah…

$L = 6 s^{2}$

$1.014 = 6 s^{2}$

$s^{2} = \frac{1.014}{6} = 169$

$s = \sqrt{169} = 13$

21. Diketahui kubus ABCD.EFGH memiliki volume 1 liter. Jarak titik F ke garis AC adalah ….cm

$V = s^{3} = 1$

$L = 1000 c m^{3}$

$\Rightarrow s = 10 c m$

Perhatikan gambar berikut:

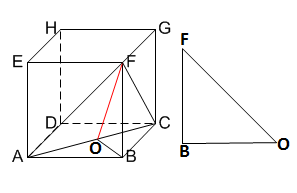
Perhatikan bahwa $A C = A F = C F =$ = Diagonal ruang $= 10 \sqrt{2}$ cm

Dengan demikian segitiga $A C F$ sama sisi. Oleh karena itu garis $F O$ tegak lurus terhadap garis $A C$

$B O = \frac{1}{2} B D = 5 \sqrt{2} C M$

$F O$ adalah jarak $F$ ke garis $A C$ . Perhatikan segitiga $F B O$

$F O = \sqrt{F B^{^{2}} + O B^{2}}$

$= \sqrt{{(10)}^{2} + {(5 \sqrt{2})}^{2}}$ $= \sqrt{100 + 50}$ $= \sqrt{150}$ $= 5 \sqrt{6}$ cm

22. ABCD.EFGH adalah sebuah kubus. Jika $α$ adalah sudut antara diagonal AG dan rusuk AD, nilai cos ∝ $α = \dots$

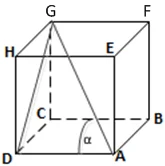
misalkan panjang rusuk kubus adalah a cm

DH=a√2 cm
AH = a√3 cm

Perhatikan segitiga ADH adalah segitiga siku-siku di D

cos ∝ = AD/AH
= a / a√3
= 1/3 √3 cm

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Tetrahedron geometri adalah bentuk geometrik 3 dimensi. Ini adalah polihedron terkecil. Hal ini terdiri 4 wajah segitiga, 3 dari yang bergabung di setiap sudut. Angka ini digunakan secara luas dalam arsitektur dan seni modern. Tetrahedron juga digunakan untuk memecahkan masalah geometris yang rumit. Klik disini untuk mengetahui lebih lanjut (akan membuka layar baru).

Bacaan Lainnya

Sumber bacaan: Pioneer Mathematics

Rumus Kubus Berserta Contoh Soal dan Jawaban

Kubus (rumus geometri)

Rumus Kubus

Luas permukaan

Volume

Diagonal sisi

Diagonal sisi seluruhnya

Diagonal ruang

Diagonal ruang seluruhnya

Luas bidang diagonal

Luas bidang diagonal seluruhnya

Contoh Soal dan Jawaban Kubus

1. Sebuah lemari es (kulkas) besar yang memiliki panjang, lebar dan sisinya sama yaitu 2 m, Hitunglah berapa volume lemari es tersebut?

2. Diketahui sebuah kubus memiliki rusuk sepanjang 12 cm. Tentukan volume kubus tersebut!

3. Hitunglah volume balok yang berukuran panjang 29 cm, lebar 12 cm, dan tinggi 8 cm!

4. Hitung Volum kubus yang mempunyai rusuk 9 cm !

5. Hitung volume kubus jika luas salah satu sisinya 9 cm² !

6. Volume sebuah kubus adalah 125 cm³. Hitung panjang rusuk kubus tersebut!

7. Hitunglah luas permukaan kubus dengan panjang setiap rusuknya sebagai berikut:
a. 4 cm
b. 7 cm
c. 10 cm
d. 12 cm

8. Hitung Luas permukaan kubus dengan panjang rusuk 7 cm !

9. Hitung Luas permukaan kubus jika luas salah satu sisinya 10 cm² !

10. Panjang rusuk suatu kubus adalah 15 cm. Berapakah volume bangun tersebut?

11. Volume sebuah kubus adalah 729 cm³. Berapakah rusuk kubus tersebut?

12. Sebuah kubus dengan rusuk 20 cm dipotong-potong menjadi kubus kecil dengan volume masing-masing 1.000 cm³. Tentukan jumlah kubus kubus kecil yang dihasilkan!

13. Sebuah wadah berbentuk kubus dengan volume 343 cm³. Berapakah panjang rusuk wadah tersebut?

14. Berapakah panjang kawat yang diperlukan untuk membuat kubus dengan volume 512 cm³?

15. Tony menuangkan air ke dalam wadah berbentuk kubus dengan rusuk 14 cm. Ternyata air yang dituangkan Andi hanya memenuhi setengah wadah tersebut. Berapa banyak air yang dituangkan Tony?

16. Diketahui panjang rusuk sebuah kubus adalah 16 cm. Jika kubus tersebut dipotong-potong menjadi kubus kecil-kecil dengan panjang rusuk masing-masing 4 cm, berapakah jumlah kubus kecil yang dihasilkan?

17. Berapa luas diagonal bujursangkar dengan rusuk 10 cm? (diketahui √2 = 1,414)

18. Hitunglah luas bidang diagonal sebuah kubus yang mempunyai panjang rusuk 24 cm! (diketahui √2 = 1,414)

19. Jessica mempunyai kertas untuk membungkus kado seluas 1,5 m². Kertas tersebut untuk membungkus kado berbentuk kubus dengan ukuran panjang rusuk 45 cm, sisa kertas terluas adalah…. cm²

20. Luas permukaan kubus adalah 1.014 $c m^{2}$ . Panjang rusuk kubus adalah…

21. Diketahui kubus ABCD.EFGH memiliki volume 1 liter. Jarak titik F ke garis AC adalah ….cm

22. ABCD.EFGH adalah sebuah kubus. Jika $α$ adalah sudut antara diagonal AG dan rusuk AD, nilai cos ∝ $α = \dots$

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Bacaan Lainnya

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

Rumus Kubus Berserta Contoh Soal dan Jawaban

Kubus (rumus geometri)

Rumus Kubus

Luas permukaan

Volume

Diagonal sisi

Diagonal sisi seluruhnya

Diagonal ruang

Diagonal ruang seluruhnya

Luas bidang diagonal

Luas bidang diagonal seluruhnya

Contoh Soal dan Jawaban Kubus

1. Sebuah lemari es (kulkas) besar yang memiliki panjang, lebar dan sisinya sama yaitu 2 m, Hitunglah berapa volume lemari es tersebut?

2. Diketahui sebuah kubus memiliki rusuk sepanjang 12 cm. Tentukan volume kubus tersebut!

3. Hitunglah volume balok yang berukuran panjang 29 cm, lebar 12 cm, dan tinggi 8 cm!

4. Hitung Volum kubus yang mempunyai rusuk 9 cm !

5. Hitung volume kubus jika luas salah satu sisinya 9 cm2 !

6. Volume sebuah kubus adalah 125 cm3. Hitung panjang rusuk kubus tersebut!

7. Hitunglah luas permukaan kubus dengan panjang setiap rusuknya sebagai berikut: a. 4 cm b. 7 cm c. 10 cm d. 12 cm

8. Hitung Luas permukaan kubus dengan panjang rusuk 7 cm !

9. Hitung Luas permukaan kubus jika luas salah satu sisinya 10 cm2 !

10. Panjang rusuk suatu kubus adalah 15 cm. Berapakah volume bangun tersebut?

11. Volume sebuah kubus adalah 729 cm³. Berapakah rusuk kubus tersebut?

12. Sebuah kubus dengan rusuk 20 cm dipotong-potong menjadi kubus kecil dengan volume masing-masing 1.000 cm³. Tentukan jumlah kubus kubus kecil yang dihasilkan!

13. Sebuah wadah berbentuk kubus dengan volume 343 cm³. Berapakah panjang rusuk wadah tersebut?

14. Berapakah panjang kawat yang diperlukan untuk membuat kubus dengan volume 512 cm³?

15. Tony menuangkan air ke dalam wadah berbentuk kubus dengan rusuk 14 cm. Ternyata air yang dituangkan Andi hanya memenuhi setengah wadah tersebut. Berapa banyak air yang dituangkan Tony?

16. Diketahui panjang rusuk sebuah kubus adalah 16 cm. Jika kubus tersebut dipotong-potong menjadi kubus kecil-kecil dengan panjang rusuk masing-masing 4 cm, berapakah jumlah kubus kecil yang dihasilkan?

17. Berapa luas diagonal bujursangkar dengan rusuk 10 cm? (diketahui √2 = 1,414)

18. Hitunglah luas bidang diagonal sebuah kubus yang mempunyai panjang rusuk 24 cm! (diketahui √2 = 1,414)

19. Jessica mempunyai kertas untuk membungkus kado seluas 1,5 m². Kertas tersebut untuk membungkus kado berbentuk kubus dengan ukuran panjang rusuk 45 cm, sisa kertas terluas adalah…. cm²

20. Luas permukaan kubus adalah 1.014 cm2cm2. Panjang rusuk kubus adalah…

21. Diketahui kubus ABCD.EFGH memiliki volume 1 liter. Jarak titik F ke garis AC adalah ….cm

22. ABCD.EFGH adalah sebuah kubus. Jika ∝ adalah sudut antara diagonal AG dan rusuk AD, nilai cos ∝=…

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Bacaan Lainnya

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

5. Hitung volume kubus jika luas salah satu sisinya 9 cm² !

6. Volume sebuah kubus adalah 125 cm³. Hitung panjang rusuk kubus tersebut!

7. Hitunglah luas permukaan kubus dengan panjang setiap rusuknya sebagai berikut:
a. 4 cm
b. 7 cm
c. 10 cm
d. 12 cm

9. Hitung Luas permukaan kubus jika luas salah satu sisinya 10 cm² !

20. Luas permukaan kubus adalah 1.014 $c m^{2}$ . Panjang rusuk kubus adalah…

22. ABCD.EFGH adalah sebuah kubus. Jika $α$ adalah sudut antara diagonal AG dan rusuk AD, nilai cos ∝ $α = \dots$