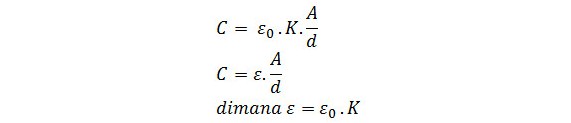Rumus Kapasitas Kapasitor

Untuk penjelasan Kapasitas Kapasitor sendiri ialah kemampuan Kapasitor yang dapat menyimpan suatu Muatan Listrik dan Kapasitas Kapasitor ini bisa didefinisikan sebagai suatu perbandingan tetap antara muatan Q yang bisa disimpan di dalam Kapasitor dengan Beda Potensial diantara Kedua Konduktornya. Berikut rumus kapasitas kapasitor:

Rumus Mencari Kapasitas Kapasitor

C = Q/V

yang diamana:
C = kapasitas kapasitor (Farad)
Q = muatan listrik yang disimpan (Coulomb)
V = beda potensial kedua ujungnya (Volt)

Nilai Kapasitansi Kapasitor tidak akan selalu bergantung pada Nilai Q dan V karena Besaran Nilai Kapasitansi sebuah Kapasitor itu tergantung pada Bentuk, Posisi dan Ukuran dari kedua keping dan jenis material insulator (pemisahnya).

Rumus Kapasitas Kapasitor Keping Sejajar

Yang dimaksud dengan Kapasitor Keping Sejajar ini adalah sebuah Kapasitor yang terdiri dari 2 buah keping konduktor yang mempunyai luas yang sama dan dipasang secara sejajar.

Untuk Rumus Mencari Kapasitor Keping Sejajar bisa kalian lihat dibawah ini:

C = є0 A/d

Dimana:

C = kapasitas kapasitor (dalam satuan farad)
εo = permitivitas ruang hampa, senilai 8,85.10-12 C2/N.m2
A = luas penampang masing-masing keping (dalam satuan m2)
d = jarak antar keping (dalam satuan m)

Rumus Kapasitas Kapasitor Keping Sejajar diatas dipakai jika antara Keping itu berisi Udara, namun jika antara kepingnya itu diisi oleh medium dielektrik lain seperti keramik, porselen dan miki yang memiliki Koefiensi Dielektrikum K, maka Rumusnya berganti seperti dibawah ini:

Rumus Kapasitas Kapasitor Bentuk Bola

Selain Kedua Rumus tersebut, terdapat satu rumus lagi yang sering digunakan untuk mencari dan menghitung Kapasitor, yakni Rumus Kapasitas Kapasitor dalam bentuk bola. Dan untuk Besarnya Kapasitas Kapasitor dalam bentuk bola tersebut bisa kalian lihat rumusnya dibawah ini:

C = 4 . π . ε0 . R

yang dimana:
C = kapasitas kapasitor (Farad)
ε0 = permivitas ruang hampa = 8,85.10-12 C2/N.m2

Rumus kapasitas kapasitor kondensator elko — Kapasitor elektrolit aluminium dengan elektrolit non-padat memiliki berbagai gaya, ukuran dan seri. Sumber foto: Wikimedia Commons

Kapasitor adalah

Kondensator atau sering disebut sebagai kapasitor adalah suatu alat yang dapat menyimpan energi di dalam medan listrik, dengan cara mengumpulkan ketidakseimbangan internal dari muatan listrik.

Jenis berdasarkan kegunaannya kondensator dibagi dalam

Kondensator tetap (nilai kapasitasnya tetap tidak dapat diubah)
Kondensator elektrolit (Electrolite Condenser = Elco)
Kondensator variabel (nilai kapasitasnya dapat diubah-ubah)

Karakteristik kondensator atau kapasitor

Macam – Macam Kapasitor itu memiliki beberapa macam bentuk dan ukuran karena tergantung dari Kapasitas, Tegangan Kerja dan Faktor lainnya.

Tipe Jangkauan Toleransi (%) Tegangan AC lazim (V) Tegangan DC lazim (V) Koefisien suhu (ppm/C) Frekuensi pancung $f_{R}$ (MHz) Sudut rugi ( $\tan \;\delta$ ) Resistansi bocoran

**Karakteristik Kondensator**
Tipe	Jangkauan	Toleransi (%)	Tegangan AC lazim (V)	Tegangan DC lazim (V)	Koefisien suhu (ppm/C)	Frekuensi pancung $f_{R}$ (MHz)	Sudut rugi ( $\tan \;\delta$ )	Resistansi bocoran (Ω)	Stabilitas
Kertas	10 nF – 10 uF	± 10%	500 V	600 V	300 ppm/C	0,1 MHz	0,01	10⁹ Ω	lumayan
Mika perak	5 pF – 10 nF	± 0,5%	–	400 V	100 ppm/C	10 MHz	0,0005	10¹¹ Ω	Baik sekali
Keramik	5 pF – 1 uF	± 10%	250 V	400 V	30 ppm/C	10 MHz	0,01	10⁸ Ω	Baik
Polystyrene	50 pF – 500 nF	± 1%	150 V	500 V	-150 ppm/C	10 MHz	0,0005	10¹² Ω	Baik sekali
Polyester	100 pF – 2 uF	± 5%	400 V	400 V	400 ppm/C	1 MHz	0,001	10¹¹ Ω	Cukup
Polypropylene	1 nF – 100 uF	± 5%	600 V	900 V	170 ppm/C	1 MHz	0,0005	10¹⁰ Ω	Cukup
Elektrolit aluminium	1 uF – 1 F	± 50%	Terpolarisasi	400 V	1500 ppm/C	0,05 MHz	0,05	10⁸ Ω	Cukup
Elektrolit tantalum	1 uF – 2000 uF	± 10%	Terpolarisasi	60 V	500 ppm/C	0,1 MHz	0,005	10⁸ Ω	Baik

4 Jenis Kapasitor Berdasarkan Bahan dan Fungsinya

Jenis Jenis Kapasitor Menurut Bahan Pembuat dan Fungsi Kapasitornya, untuk penjelasan lebih lengkapnya bisa kalian lihat dibawah ini :

1. Kapasitor Keramik

Jenis Kapasitor Keramik ini merupakan sebuah Kapasitor yang mempunyai bahan Keramik dan Kapasitor Keramik ini banyak dipakai didalam Komponen Aplikasi Audio ke RF. Lalu Kapasitor Keramik juga paling banyak dan paling umum dipakai didalam Rangkaian Elektronik.

Untuk Cara Membaca Kapasitor Keramik sangatlah mudah karena bisa kalian lihat contohnya seperti ini : Jika Anda memiliki sebuah Kapasitor dengan kode yang dimiliki 103 maka arti dari kode tersebut adalah 10 dan 3 angka dibelakang menjadi 10.000 pF yang jika didalam Satuan lebih besar menjadi 10 nF (Satuan Nano Farad).

2. Kapasitor Tantalum

Macam Kapasitor Yang Kedua adalah Kapasitor Tantalum. Kapasitor Tantanum ini lebih mirip dengan Kapasitor Elektrolit, hanya saja Kapasitor Tantalum ini mempunyai kapasitansi dan kepopuleran yang cukup tinggi. Hanya saja kelemahan dari Kapasitor Tantanum ini yang mesti kalian ketahui ialah sering meledak jika digunakan terus menerus di tekanan yang tinggi.

Adapun didalam Kelebihan Kapasitor Tantalum ini antara lain mempunyai bentuk Komponen yang kecil, tetapi kapasitansinya mempunyai nilai yang besar sehingga sangat efisien jika digunakan.

Selain itu Kapasitor Tantalum ini bisa dipakai pada Range Frekuensi yang lebar dan Frekuensi yang tinggi. Kelebihan selanjutnya ialah dapat dipakai dan tahan terhadap Suhu dari -55C sampai +125C sehingga sangat cocok jka dipakai di rangkaian yang diharuskan mempunyai daya tahan yang tinggi.

3. Kapasitor Elektrolit

Kapasitor Elektrolit ini dapat dikatakan sebagai kapasitor yang Terpolarisasi dan bisa memberikan hasil suatu Kapasitansi Tinggi sampai diatas 1 Mikrofarad. Perlu diketahui juga bahwa didalam Kapasitor Elektrolit ini banyak sekali dipakai untuk Aplikasi Pasokan Listrik Frekuensi Rendah dan dapat dipakai juga pada Aplikasi Kopling Audio.

Namun perlu diperhatikan kepada kalian bahwa pemasangan Kapasitor Elektrolit ini harus benar – benar berhati hati karena Kapasitor Elektrolit ini mempunyai Polaritas (+) dan (-), jika pemasangannya terbalik maka akan sangat berakibat fatal karena akibatnya Kapasitor Elektrolit ini akan meledak. Selain itu Nilai Kapasitas dari Kapasitor Elektrolit ini bisanya juga besar dengan tegangan yang tinggi juga.

4. Kapasitor Mika

Kemudian untuk Kapasitor Mika ini merupakan sebuah Kapasitor yang sudah jarang sekali dipakai, hal ini dikarenakan Kapasitor Mika sudah kalah populer dengan Kapasitor Tantalum dan Kapasitor Elektrolit.

Padahal jika dilihat dari Stabilitasnya sendiri cukup bagus dan jika dilihat dari Kapasitansinya sendiri Kapasitor Mika ini mempunyai Kapasitansi yang cukup tinggi, hingga angka 1000 pikofarad.

Selain itu, pemakaian Kapasitor Mika ini biasanya digunakan di Rangkaian RF dengan Frekuensi yang tinggi dan hal ini dikarenakan Toleransi yang rendah dan ketahanan Kapasitor Mika terhadap suhu yang sangat baik. Sesuai dengan namanya, maka sudah jelas bahwa Bahan Kapasitor Mika ini telah dibuat dengan menggunakan Bahan Mika. Lalu untuk Fungsi Kapasitor Mika antara lain sebagai Osilator RF, Filter, dan Kopling.

Fungsi dan Kegunaan Kapasitor

Berikut adalah fungsi dan kegunaan kapasitor:

1. Digunakan untuk menghemat daya listrik yang ada didalam Lampu Neon.

2. Sebagai pembangkit frekuensi yang biasanya digunakan didalam Rangkaian suatu Antena.

3. Sebagai suatu penghubung (Kopling) Amplifier tingkat rendah ketingkat yang lebih tinggi.

4. Digunakan sebagai Penyaring (Filter) yang biasanya dipakai di Sistem Radio, Amplifier, TV dan lain lain. Sebagai contohnya jika didalam Radio, Kapasitor dipakai untuk menghambat (Menyaring) gangguan2 dari luar.

Contoh Soal dan Jawaban Kapasitor dengan menggunakan Rumus Kapasitas Kapasitor

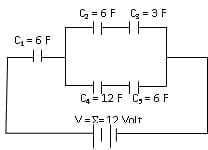
Besarnya muatan pada kapasitor C5 adalah…

a. 36 Coulomb
b. 24 Coulomb
c. 12 Coulomb
d. 6 Coulomb
e. 4 Coulomb

Pembahasan Soal :

1/C seri1 = 1/c2+1/c3 = 1/6 + 1/3 = 1/6 + 2/6 = 3/6 ——> C seri1= 2 F

1/C ser2 = 1/c4 + 1/c5 = 1/12 + 1/6 = 1/12 + 2/12 = 3/12——-> C seri2 = 4 F

C paralel = C seri1 + C seri 2 = 2 F + 4 F = 6 F

1/C seri 3 = 1/c1 = 1/C paralel = 1/6 + 1/6 = 2/6 ——> Cseri 3 = C total = C pengganti 5 Kapsitor = 3 F

Q Total = C total X V total = 3 x 12 = 36 Coulomb = Q 1 = Q 2,3,4,5 = 36 Coulomb

V1 = Q1/C1 = 36/6 = 6 Volt——> V2,3,4,5 = Vtotal – V1 = 12-6 = 6 Volt

V2,3,4,5 =V Paralel= V2,3= V4,5 = 6 Volt-

Q2,3= V2,3 X C2,3 = 6 X 12 = 12 Coulomb

Q4,5 = V4,5 X C4,5 = V4,6 X C seri 2 = 6 x 4 = 24 Coulomb

Q Seri = Q4,5 = Q4 = Q5 = 24 Coulomb

Jawaban yang benar (b) 24 Coulomb

Kapasitas kapasitor keping sejajar menjadi lebih kecil jika…

1. Luas penampang keping kapasitor (A) diperkecil
2. Jarak antar keping kapasitor (d) ditingkatkan
3. Menggunakan bahan dielektrik dengan permitivitas lebih besar dari permitivitas ruang hampa (є0)

Penjelasan:

Besar kapasitas kapasitor dengan bentuk kapasitor dua keping, besarnya kapasitas kapasitor adalah:

C = є0 A/d

Dimana:

Disini terlihat bahwa:

– kapasitas kapasitor berbanding lurus dengan luas kepingnya. Sehingga kapasitas kapasitor akan naik bila luas keping ditingkatkan, dan akan turun bila luas keping diturunkan

– kapasitas kapasitor berbanding terbalik dengan jarak kepingnya. Sehingga kapasitas kapasitor akan naik bila jarak keping didekatkan, dan akan turun bila jarak keping dijauhkan

Bila diantara keping kapasitor bukan ruang hampa tetapi benda dielektrik, tidak digunakan permitivitas vakum (є0), melainkan permitivitas statis dari bahan tersebut (єs), yang besarnya adalah sebesar:

єs = єr. є0

Dimana єr adalah konstanta dielektrik

Sehingga kapasitas kapasitor tersebut menjadi tergantung dari besar kecilnya konstanta dielektrik benda di antara kedua keping kapasitor. Besar dari єr lebih kecil dari 1 sehingga besar dari permitivitas medium (єs) akan lebih kecil dari permitivitas ruang hampa (є0), dan demikian pula kapasitas kapasitor pun mengecil.

Jika terdapat sebuah Kapasitor dengan mempunyai besaran kapasitas sebesar 0.8 μF yang dimuati oleh sebuah Baterai berkapasitas 20 Volt. Maka berapakah Muatan yang tersimpan didalam Kapasitor tersebut?

Diketahui:
C = 0.8 μF sama dengan 8 x 10^-7 F
V = 20 Volt (V)

Ditanya:
Berapakah nilah Q ?

Jawaban:
C = Q / V sehingga Q = C x V
Q = 8 x 10^-7 x 20
Q = 1.6 x 10^-5 coulomb

Terdapat sebuah Kapasitor Keping Sejajar dengan mempunyai Luas tiap kepingnya sebesar 2000 cm² dan terpisah sejauh 2 centimeter antara satu dengan lain. Berapakah nilai dari Kapasitas Kapasitor tersebut ?

Jawaban:
C = 8,85.10^-12 . (0,2./0,002)
C = 8,85.10^-12 x 100
C = 8,85.10^-10 farad

Tiga buah kapasitor C1, C2, dan C3 dengan kapasitas masing-masing 2 µF, 1 µF, 5 µF disusun seri. Kemudian dihubungkan dengan sumber tegangan sehingga kapasitor C2 mempunyai beda potensial sebesar 4 Volt. Muatan pada kapasitor C3 adalah…

A. 3 µC
B. 4 µC
C. 8 µC
D. 12 µC
E. 24 µC

Pembahasan:
Diketahui:
C1 = 2 µF
C2 = 1 µF
C3 = 5 µF
V2 = 4 V
Ditanya: Q3 = …
Jawab:
Q3 = Q2 = C2 . V2 = 1 µF . 4 V = 4 µC
Jawaban: B.

Jika 3 buah kapasitor C1,C2,C3 dengan kapasitansi masing masing 2 uf, 3 uf, dan 6 uf disusun seri, kemudian dihubungkan ke sumber tegangan 6 volt. Maka berapa besar muatan yang tersimpan pada kapasitor C2?

Jawaban:

Pendahuluan
Ini merupakan persoalan listrik statis terkait rangkaian kapasitor seri. Diminta untuk menentukan muatan yang tersimpan di salah satu kapasitor.

Pembahasan
Diketahui

C₁ = 2 μF
C₂ = 3 μF
C₃ = 6 μF

Tegangan sumber = 6 volt

Ditanya

Besar muatan yang tersimpan pada kapasitor C₂ (sebutlah sebagai Q₂, dalam coulomb)

Penyelesaian

Step-1 menghitung kapasitor total rangkaian seri 1/C = 1/C₁ + 1/C₂ + 1/C₃
1/C = 1/2 + 1/3 + 1/6
Satuan kapasitas kapasitor dalam mikrofarad.

1/C = 3/6 + 2/6 + 6/6
1/C = 6/6
Diperoleh kapasitas total C = 1 μF.

Step-2 menghitung besar muatan total Q
Rangkaian seri kapasitor dihubungkan dengan sumber tegangan 6 volt.

Muatan totalnya adalah Q = C.V
Q = (1 μF)(6 V)
Q = 6 μC

Step-3 menghitung besar muatan yang tersimpan pada kapasitor C₂

Sesuai prinsip rangkaian kapasitor secara seri, besar muatan yang tersimpan di tiap-tiap kapasitor adalah sama dengan besarnya muatan total.

Sehingga, besar muatan yang tersimpan pada kapasitor C₂ adalah Q2 = Q = 6 μC

Alternatif Pertanyaan

(a). Berapa besar tegangan di tiap-tiap kapasitor?

Karena muatan pada tiap-tiap kapasitor seri adalah sama, maka berlaku V₁ : V₂ : V₃ = 1/C₁ : 1/C₂ : 1/C₃

Kalikan 6.

V₁ : V₂ : V₃ = 3 : 2 : 1 ⇒ total angka banding adalah 3 + 2 + 1 = 6.
V₁ = ³/₆ x 6 volt = 3 volt
V₂ = ²/₆ x 6 volt = 2 volt
V₃ = ¹/₆ x 6 volt = 1 volt

(b). Berapa besar energi yang tersimpan di tiap-tiap kapasitor?
W = ¹/₂ CV²
W₁ = ¹/₂ x C₁ x V₁²
W₁ = ¹/₂ x (2 μF) x (3 V)² ⇒ W₁ = 9 μJ
W₂ = ¹/₂ x C₂ x V₂²
W₂ = ¹/₂ x (3 μF) x (2 V)² ⇒ W₁ = 6 μJ
W₃ = ¹/₂ x C₃ x V₃²
W₃ = ¹/₂ x (6 μF) x (1 V)² ⇒ W₁ = 3 μJ

Kesimpulan
Dari langkah-langkah pengerjaan di atas, diperoleh muatan yang tersimpan pada kapasitor C₂ sebesar Q2 = Q = 6 μC

Bacaan Lainnya

Sumber bacaan: Electronics Tutorials, How Stuff Works, Spark Fun, Explain That Stuff

Rumus Kapasitas Kapasitor – Kapasitor: Elektrolit, Keramik, Tantalum, Mika – Soal dan Jawaban

Rumus Kapasitas Kapasitor

Rumus Mencari Kapasitas Kapasitor

Rumus Kapasitas Kapasitor Keping Sejajar

Rumus Kapasitas Kapasitor Bentuk Bola

Kapasitor adalah

Jenis berdasarkan kegunaannya kondensator dibagi dalam

Karakteristik kondensator atau kapasitor

4 Jenis Kapasitor Berdasarkan Bahan dan Fungsinya

1. Kapasitor Keramik

2. Kapasitor Tantalum

3. Kapasitor Elektrolit

4. Kapasitor Mika

Fungsi dan Kegunaan Kapasitor

Contoh Soal dan Jawaban Kapasitor dengan menggunakan Rumus Kapasitas Kapasitor

Besarnya muatan pada kapasitor C5 adalah…

Kapasitas kapasitor keping sejajar menjadi lebih kecil jika…

Jika terdapat sebuah Kapasitor dengan mempunyai besaran kapasitas sebesar 0.8 μF yang dimuati oleh sebuah Baterai berkapasitas 20 Volt. Maka berapakah Muatan yang tersimpan didalam Kapasitor tersebut?

Terdapat sebuah Kapasitor Keping Sejajar dengan mempunyai Luas tiap kepingnya sebesar 2000 cm² dan terpisah sejauh 2 centimeter antara satu dengan lain. Berapakah nilai dari Kapasitas Kapasitor tersebut ?

Tiga buah kapasitor C1, C2, dan C3 dengan kapasitas masing-masing 2 µF, 1 µF, 5 µF disusun seri. Kemudian dihubungkan dengan sumber tegangan sehingga kapasitor C2 mempunyai beda potensial sebesar 4 Volt. Muatan pada kapasitor C3 adalah…

Jika 3 buah kapasitor C1,C2,C3 dengan kapasitansi masing masing 2 uf, 3 uf, dan 6 uf disusun seri, kemudian dihubungkan ke sumber tegangan 6 volt. Maka berapa besar muatan yang tersimpan pada kapasitor C2?

Bacaan Lainnya

Rahasia Kehidupan Harimau: Mengenal Lebih Dekat dengan Sang Raja…

Asteroid Apophis “Dewa Kekacauan” dan Bumi: data baru pada…

Keajaiban Bintang Jatuh (Shooting Stars): Gemerlap Meteor di Langit…

Tinggalkan Balasan Batalkan balasan

Rumus Kapasitas Kapasitor – Kapasitor: Elektrolit, Keramik, Tantalum, Mika – Soal dan Jawaban

Rumus Kapasitas Kapasitor

Rumus Mencari Kapasitas Kapasitor

Rumus Kapasitas Kapasitor Keping Sejajar

Rumus Kapasitas Kapasitor Bentuk Bola

Kapasitor adalah

Jenis berdasarkan kegunaannya kondensator dibagi dalam

Karakteristik kondensator atau kapasitor

4 Jenis Kapasitor Berdasarkan Bahan dan Fungsinya

1. Kapasitor Keramik

2. Kapasitor Tantalum

3. Kapasitor Elektrolit

4. Kapasitor Mika

Fungsi dan Kegunaan Kapasitor

Contoh Soal dan Jawaban Kapasitor dengan menggunakan Rumus Kapasitas Kapasitor

Besarnya muatan pada kapasitor C5 adalah…

Kapasitas kapasitor keping sejajar menjadi lebih kecil jika…

Jika terdapat sebuah Kapasitor dengan mempunyai besaran kapasitas sebesar 0.8 μF yang dimuati oleh sebuah Baterai berkapasitas 20 Volt. Maka berapakah Muatan yang tersimpan didalam Kapasitor tersebut?

Terdapat sebuah Kapasitor Keping Sejajar dengan mempunyai Luas tiap kepingnya sebesar 2000 cm2 dan terpisah sejauh 2 centimeter antara satu dengan lain. Berapakah nilai dari Kapasitas Kapasitor tersebut ?

Tiga buah kapasitor C1, C2, dan C3 dengan kapasitas masing-masing 2 µF, 1 µF, 5 µF disusun seri. Kemudian dihubungkan dengan sumber tegangan sehingga kapasitor C2 mempunyai beda potensial sebesar 4 Volt. Muatan pada kapasitor C3 adalah…

Jika 3 buah kapasitor C1,C2,C3 dengan kapasitansi masing masing 2 uf, 3 uf, dan 6 uf disusun seri, kemudian dihubungkan ke sumber tegangan 6 volt. Maka berapa besar muatan yang tersimpan pada kapasitor C2?

Bacaan Lainnya

Rahasia Kehidupan Harimau: Mengenal Lebih Dekat dengan Sang Raja…

Asteroid Apophis “Dewa Kekacauan” dan Bumi: data baru pada…

Keajaiban Bintang Jatuh (Shooting Stars): Gemerlap Meteor di Langit…

Tinggalkan Balasan Batalkan balasan

Terdapat sebuah Kapasitor Keping Sejajar dengan mempunyai Luas tiap kepingnya sebesar 2000 cm² dan terpisah sejauh 2 centimeter antara satu dengan lain. Berapakah nilai dari Kapasitas Kapasitor tersebut ?