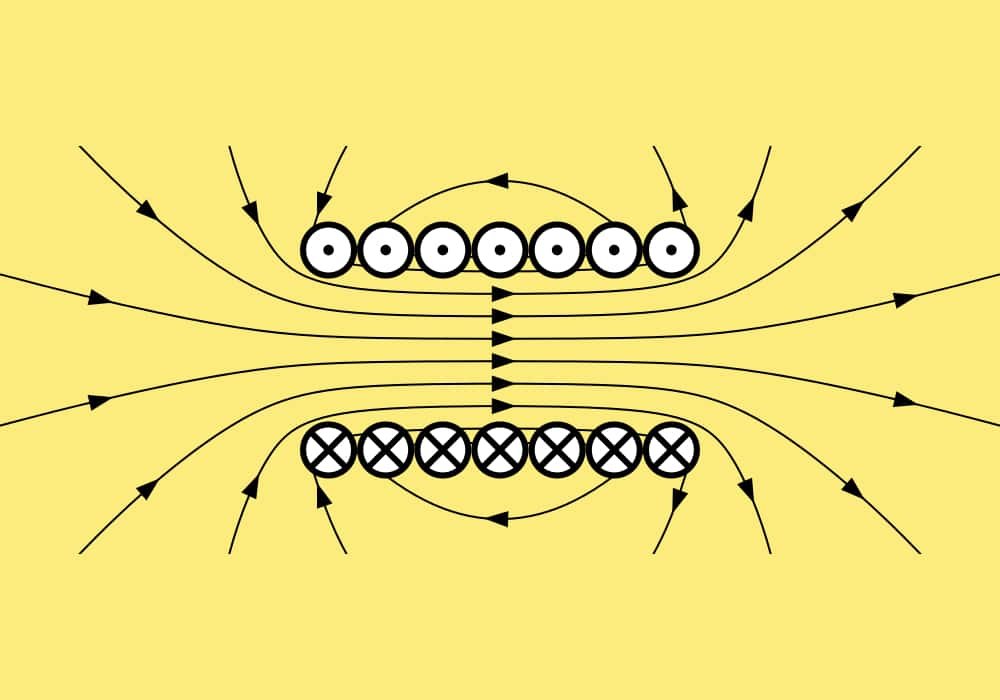
Induktansi dan Energi Medan Magnet

Induktansi adalah sifat dari rangkaian elektronika. Hal ini menyebabkan timbulnya potensial listrik secara proporsional terhadap arus yang mengalir pada rangkaian tersebut, sifat ini disebut sebagai induktansi sendiri, sedangkan apabila potensial listrik dalam suatu rangkaian ditimbulkan oleh perubahan arus dari rangkaian lain disebut sebagai induktansi bersama.

Definisi kuantitatif dari induktansi sendiri (simbol: L) adalah : $\displaystyle v= L\frac{di}{dt}$ di mana v adalah GGL yang ditimbulkan dalam volt dan i adalah arus listrik dalam ampere. Bentuk paling sederhana dari rumus tersebut terjadi ketika arus konstan sehingga tidak ada GGL yang dihasilkan atau ketika arus berubah secara konstan (linier) sehingga GGL yang dihasilkan konstan (tidak berubah-ubah).

Istilah ‘induktansi’ sendiri pertama kali digunakan oleh Oliver Heavside pada Februari 1886. Sedang penggunaan simbol L kemungkinan ditujukan sebagai penghormatan kepada Heinrich Lenz, seorang fisikawan ternama. Satuan induktansi dalam Satuan Internasional adalah weber per ampere atau dikenal pula sebagai henry (H), untuk menghormati Joseph Henry seorang peneliti yang berkontribusi besar terhadap ilmu tentang magnetisme. 1 H = 1 Wb/A.

Induktansi muncul karena adanya medan magnet yang ditimbulkan oleh arus listrik (dijelaskan oleh Hukum Ampere). Supaya suatu rangkaian elektronika mempunyai nilai induktansi, sebuah komponen bernama induktor digunakan di dalam rangkaian tersebut, induktor umumnya berupa kumparan kabel/tembaga untuk memusatkan medan magnet dan memanfaatkan GGL yang dihasilkannya.

Bentuk umum dari K buah rangkaian dengan arus i_m dan tegangan v_m adalah

\displaystyle v_{m}=\sum\limits_{n=1}^{K}L_{m,n}\frac{di_{n}}{dt}.

Koefisien L yang digunakan pada rumus di atas merupakan matriks simetris, rumus tersebut berlaku selama tidak menggunakan bahan yang bisa menjadi magnet, jika tidak maka besaran L merupakan fungsi dari besaran arus (induktansi non-linier).

Penerapan Persamaan Maxwell untuk induktansi

Rumus umum di atas merupakan penerapan dari Persamaan Maxwell jika rangkaian tersebut menggunakan kabel tipis.

Misal suatu rangkaian yang terdiri dari K buah kumparan kabel, masing-masing terdiri dari satu atau beberapa lilitan. Fluks magnetik yang timbul akan terangkai sebesar

\displaystyle N_{m}\Phi _{m}=\sum\limits_{n=1}^{K}L_{m,n}i_{n}.

Di mana N_m merupakan jumlah lilitan dalam kumparan m, Φ_m adalah fluks magnetik yang melalui kumparan, dan L_m,n adalah konstanta. Persamaan ini diturunkan dari Hukum Ampere—medan magnet dan fluks magnetik merupakan fungsi linier dari arus listrik. Dengan menggunakan Hukum Faraday dapat diperoleh

\displaystyle v_{m}=N_{m}\frac{d\Phi _{m}}{dt}=\sum\limits_{n=1}^{K}L_{m,n}\frac{di_{n}}{dt},

di mana v_m merupakan GGL yang terinduksi dalam rangkaian m. Rumus tersebut sesuai dengan definisi di atas bahwa koefisien L_m,n dapat diidentifikasi sebagai koefisien induktansi. Karena seluruh arus N_ni_n berperan menimbulkan fluks Φ_m, dapat pula dimengerti bahwa L_m,n sebanding dengan perkalian jumlah lilitan N_mN_n.

Induktansi dan Energi Medan Magnet

Dengan mengalikan persamaan v_m di atas dengan i_mdt dan menjumlahkan untuk semua m maka kita dapatkan energi yang di transfer sistem ini dalam satu satuan waktu dt,

\displaystyle \sum\limits_{m}^{K}i_{m}v_{m}dt=\sum\limits_{m,n=1}^{K}i_{m}L_{m,n}di_{n} \overset{!}{=}\sum\limits_{n=1}^{K}\frac{\partial W\left( i\right) }{\partial i_{n}}di_{n}.

Hal ini harus tetap sesuai dengan perubahan energi medan magnet W yang ditimbulkan oleh arus listrik. Integritas

\displaystyle\partial ^{2}W/\partial i_{m}\partial i_{n}=\partial ^{2}W/\partial i_{n}\partial i_{m}

mengharuskan L_m,n=L_n,m. Sehingga L_m,n harus merupakan matriks simetris.

Integral dari energi yang ditransfer adalah energi medan magnet sebagai fungsi dari arus,

\displaystyle W\left( i\right) =\tfrac{1}{2}\sum \limits_{m,n=1}^{K}i_{m}L_{m,n}i_{n}.

Persamaan ini juga merupakan konsekuensi dari linearitas Persamaan Maxwell. Supaya mudah mengingat perlu diperhatikan bahwa perubahan arus listrik berhubungan langsung dengan perubahan energi medan magnet. Energi ini memerlukan sumber tegangan (jika negatif, energi diambil) atau menghasilkan tegangan (jika energi positif, disalurkan).

Analoginya dalam energi mekanis untuk K = 1 dengan energi medan magnetik (1/2)Li² adalah sebuah benda dengan masa M, dengan laju u dan energi kinetiknya (1/2)Mu².

Energi dari perubahan laju (dalam hal elektronika, arus listrik) dikalikan masa benda (induktansi) diperoleh dari gaya (jika energi kinetik bertambah) atau menghasilkan gaya (jika energi kinetik berkurang).

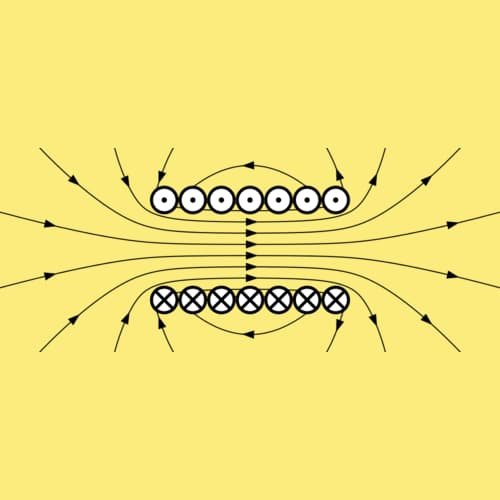
Induktor yang Berpasangan (Kopling Induktor)

Induktansi bersama muncul ketika perubahan arus dalam satu induktor menginduksi (mempengaruhi) timbulnya GGL di induktor lain yang ada di dekatnya. Mekanisme ini merupakan dasar yang sangat penting dalam cara kerja transformer, namun kadang kala induksi bersama yang bisa terjadi antara konduktor yang berdekatan malah menjadi hal yang harus dihindari dalam suatu rangkaian.

Induktansi bersama, M, juga merupakan ukuran saling induksi antara dua buah induktor. Induktansi bersama oleh rangkaian i kepada rangkaian j dihitung menggunakan integral ganda Rumus Neumann.

Induktansi bersama memiliki hubungan persamaan:

M_{21} = N_1 N_2 P_{21} \!

yang di mana:

M_{21}

adalah nilai induktansi bersama, dan tanda 21 menunjukkan keterkaitan GGL yang terinduksi dalam kumparan 2 disebabkan oleh perubahan arus dalam kumparan 1.

N₁ adalah jumlah lilitan pada kumparan 1,

N₂ adalah jumlah lilitan pada kumparan 2,

P₂₁ adalah permeansi ruang di mana fluks magnetik berada.

Induktansi bersama juga memiliki keterkaitan dengan koefisien kopling. Koefisien kopling bernilai antara 1 dan 0, koefisien kopling digunakan sebagai indikator keterkaitan antara induktor yang dipasangkan (dikopling).

M = k \sqrt{L_1 L_2} \!

yang di mana:

k adalah koefisien kopling dan 0 ≤ k ≤ 1,

L₁ adalah nilai induktansi kumparan pertama, dan

L₂ adalah nilai induktansi kumparan kedua.

Jika nilai induktansi bersama, M, sudah diketahui, maka nilai ini dapat digunakan untuk memprediksi sifat dari suatu rangkaian:

V_1 = L_1 \frac{dI_1}{dt} - M \frac{dI_2}{dt}

yang di mana:

V₁ adalah tegangan dalam induktor yang dihitung,

L₁ adalah induktansi dalam induktor yang dihitung,

dI₁/dt adalah arus (diturunkan atas waktu) yang mengalir dalam induktor yang dihitung,

dI₂/dt adalah arus (diturunkan atas waktu) yang mengalir dalam induktor yang dikopling (diinduksi oleh induktor pertama), dan

M adalah nilai induktansi bersama.

Tanda minus muncul karena menurut konvensi titik, kedua arus yang mengalir pada masing-masing induktor saling berlawanan arah.

Jika suatu induktor dipasangkan secara berdekatan dengan induktor lain dengan menggunakan prinsip induktansi bersama, seperti dalam transformer, maka tegangan, arus, dan jumlah lilitan dapat dihubungkan sebagai berikut:

V_\text{s} = \frac{N_\text{s}}{N_\text{p}} V_\text{p}

yang di mana:

V_s adalah tegangan pada induktor sekunder,

V_p adalah tegangan pada induktor primer (yaitu yang terhubung dengan sumber listrik),

N_s adalah jumlah lilitan pada induktor sekunder, dan

N_p adalah jumlah lilitan pada induktor primer.

Begitu pula untuk arus:

I_\text{s} = \frac{N_\text{p}}{N_\text{s}} I_\text{p}

yang di mana:

I_s adalah arus yang mengalir dalam induktor sekunder,

I_p adalah arus yang mengalir dalam induktor sekunder (yaitu yang terhubung dengan sumber listrik),

N_s adalah jumlah lilitan pada induktor sekunder, dan

N_p adalah jumlah lilitan pada induktor primer.

Perlu diperhatikan bahwa daya dari kedua induktor tersebut adalah sama. Juga persamaan di atas tidak berlaku jika kedua induktor memiliki sumber energi sendiri-sendiri (keduanya induktor primer).

Jika kedua sisi transformer merupakan rangkaian LC yang mana frekuensi tegangan menjadi penting, nilai induktansi bersama antara dua lilitan ini menentukan bentuk dari kurva renspon frekuensi. Walaupun batas-batas nilai indutansi bersama ini tidak didefinisikan, namun sering disebut sebagai loose-coupling, critical-coupling, dan over-coupling.

Jika rangkaian tersebut melalui transformer yang loose-coupling, bandwidth-nya akan sempit. Ketika nilai induktansi bersama ditingkatkan, bandwidth-nya ikut naik pula. Ketika nilai induktansi bersama telah melampaui titik kritis, respon bandwidth akan mulai menurun, frekuensi-frekuensi tengah akan teratuentasi lebih dibanding frekuensi-frekuensi samping. Kondisi ini disebut over-coupling.

Rumus Perhitungan Induktasi

Umumnya, induktansi dapat dihitung menggunakan persamaan Maxwell. Pada banyak skenario perhitungan dapat disederhanakan dari persamaan Maxwell. Jika menginginkan induksi dengan arus berfrekuensi tinggi, dengan efek kulit, arus listrik dan medan magnet pada permukaan konduktor dapat dihitung dengan menggunakan persamaan Laplace.

Walaupun konduktor yang digunakan adalah kawat tipis, induktansi sendiri masih bergantung pada jari-jari penampang kawat dan distribusi arus dalam kawat tersebut. Distribusi arus ini rata-rata konstan (pada permukaan atau badan kawat) untuk kawat tipis.

Induktansi bersama

Induktansi bersama dalam rangkaian kumparan i kepada rangkaian j dinyatakan dalam integral ganda Rumus Neumann

M_{ij}={\frac {\mu _{0}}{4\pi }}\oint _{C_{i}}\oint _{C_{j}}{\frac {d\mathbf {x} _{i}\cdot d\mathbf {x} _{j}}{|\mathbf {x} _{i}-\mathbf {x} _{j}|}}

Simbol μ₀ menunjukkan konstanta magnetik (4π×10⁻⁷ H/m), ‘C_i dan C_j adalah panjang kawat, |x_i–x_j| adalah jarak antara dua induktor.

Induktansi sendiri

Pada dasarnya induktansi sendiri dari kumparan kawat dapat dinyatakan pula dengan persamaan di atas dengan menganggap i=j. Masalahnya, 1/|x–x’| menjadi tidak terdefinisi, sehingga perlu menyatakan penampang a sebagai penampang kawat dan memperhatikan pula distribusi arus pada kawat tersebut. Sehingga ada integral untuk semua titik di mana |x–x’| ≥ a/2,

M_{ii}=L\approx \left({\frac {\mu _{0}}{4\pi }}\oint _{C}\oint _{C'}{\frac {d\mathbf {x} \cdot d\mathbf {x} '}{|\mathbf {x} -\mathbf {x'} |}}\right)_{|\mathbf {x} -\mathbf {x'} |\geq a/2}+{\frac {\mu _{0}}{4\pi }}lY

Disini a dan l menunjukkan jari-jari penampang kawat dan panjang kawat, dan Y adalah konstanta yang tergantung pada distribusi arus dalam kawat: Y = 0 ketika arus mengalir pada permukaan kawat (efek kulit), Y = 1/2 ketika arus tersebar rata dalam kawat. Nilai-nilai ini hanya perkiraan namun cukup akurat jika kawat yang dipergunakan tipis dan panjang.

Hubungan induktansi dan kapasitansi

Induktansi per satuan panjang L’ dan kapasitansi per satuan panjang C’ saling berhubungan dalam beberapa kasus jalur transmisi yang terdiri dari dua konduktor sempurna yang saling sejajar,

\displaystyle L'C'={\varepsilon \mu}.

Disini ε dan µ mewakili konstanta dielektik dan konstanta permeabilitas magnetik milik konduktor yang digunakan. Dalam hal ini tidak ada arus listrik dan medan magnet di dalam konduktor (efek kulit murni, frekuensi tinggi). Arus mengalir dari satu jalur menuju jalur yang lain. Kecepatan propagasi sinyal sejalan dengan kecepatan propagasi gelombang elektromagnetik.

Induktansi dan energi medan magnet — Induktansi dan Energi Medan Magnet – Soal dan Jawaban

Soal dan Jawaban Induktansi

Berapa ggl yang akan diinduksikan dalam sebuah induktor 100 mH di mana arus berubah dari 10 A menjadi 7 A dalam 90 ms.

Jawaban:

Induktansi diri L = 100 mH = 0,1 H, perubahan arus ∆i = 7 A – 10 A = –3 A; selang waktu t = 0,09 s. Ggl induksi diri, ε dihitung dengan
ε = –L∆i/∆t
= –0,1H (–3 A)/(0,09 s)
ε = 3,3 Volt

Sebuah kumparan berbentuk toroida memiliki luas penampang 5,0 cm², jari-jari efektif 0,10 m dan memiliki 200 lilitan. Tentukan; (a) induktansi toroida dan (b) energi magnetik yang tersimpan dalam toroida jika dialiri arus 6,0 A.

Jawaban:

Luas penampang A = 5,0 x 10^-4 m²; jari-jari r = 0,10 m; jumlah lilitan N = 200.
(a) induktansi toroida dihitung dengan persamaan,
L = μ₀N²A/l dengan l = keliling toroida = 2πr
= (4π x 10^-7)(200)²(5,0 x 10^-4 m²)/2π(0,10 m)
L = 40 μH
(b) kuat arus i = 6,0 A. Energi magnetik dalam toroida W dihitung dengan persamaan
W = ½ Li² = ½ (40 x 10^-6H)(6,0 A)²
W = 7,20 x 10^-4 J
Arus dalam suatu induksi 90 mH berubah terhadap waktu sebagai i = t² – 6t (dalam satuan SI). Tentukan besar ggl induksi pada; (a) t = 1,0 s dan t = 4,0 s dan (b) kapan ggl bernilai nol?

Jawaban:

Induktansi L = 0,09 H, kuat arus i = t² – 6t maka di/dt = 2t – 6. Besar ggl induksi dihitung dengan persamaan
ε = –Ldi/dt = –(0,09 H)(2t – 6)
ε = –0,18(t – 3)
(a) saat t = 1,0 s; ε = 0,18(1 – 3) = 0,36 V
saat t = 4,0 s; ε = –0,18(4 – 3) = –0,18 V
(b) ε = 0 maka,
0 = –0,18(t – 3)
t = 3 sekon
Jadi, ggl bernilai nol saat t = 3 s.

Sebuah kumparan dengan hambatan 40,0 ohm dan induktansi 50,0 H dialiri arus yang besarnya berubah-ubah terhadap waktu menurut persamaan i = 0,180 sin 120πt (dalam SI). Tentukan kuat arus induksi diri maksimum yang timbul pada kumparan kawat tersebut.

Jawaban:

Hambatan R = 40,0 ohm, induktansi L = 50,0 H, maka
di/dt = d/dt[0,180 sin 120πt] = 0,180(120π) cos 120πt
Karena adanya laju perubahan arus, di/dt, maka timbul ggl induksi ε yang diperoleh dari
ε = –Ldi/dt
kuat arus induksi diri i_ind dihitung dengan hukum ohm,
i_ind = ε/R = – (L/R)di/dt
i_ind = – [(50 V)/(40Ω)L])[0,180(120π) cos 120πt] Kuat arus induksi-diri maksimum adalah
i_ind,maks = – [(50 V)/(40Ω)L])[0,180(120π] i_ind,maks = 27π A

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumner bacaan: Tutor Vista, Electronics Tutorials, NCBI (National Center for Biotechnology Information), RF Cafe

Rumus Induktansi, Induktor dan Energi Medan Magnet – Soal dan Jawaban

Induktansi dan Energi Medan Magnet

Penerapan Persamaan Maxwell untuk induktansi

Induktansi dan Energi Medan Magnet