Rumus Elips atau Oval

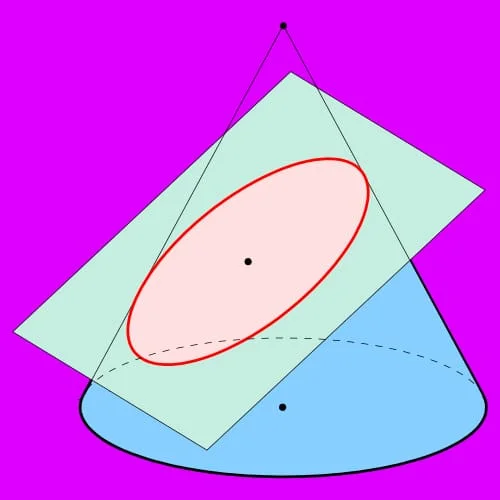
Elips adalah salah satu contoh dari irisan kerucut dan dapat didefinisikan sebagai lokus atau tempat dari semua titik, dalam satu bidang, yang memiliki jumlah jarak yang sama dari dua titik tetap yang telah ditentukan sebelumnya (disebut fokus).

Dalam matematika, sebuah elips atau oval adalah gambar yang menyerupai lingkaran yang telah dipanjangkan ke satu arah.

Dalam bahasa Indonesia, selain istilah elips atau oval, juga sering dikenal istilah sepadan, yakni bulat lonjong (atau lonjong saja), bulat bujur dan bulat panjang.

Rumus luas elips

Luas elips adalah $L=\pi ab$

Rumus keliling elips

Keliling elips adalah

Keliling I: $K\approx 2\pi {\sqrt {\frac {a^{2}+b^{2}}{2}}}$

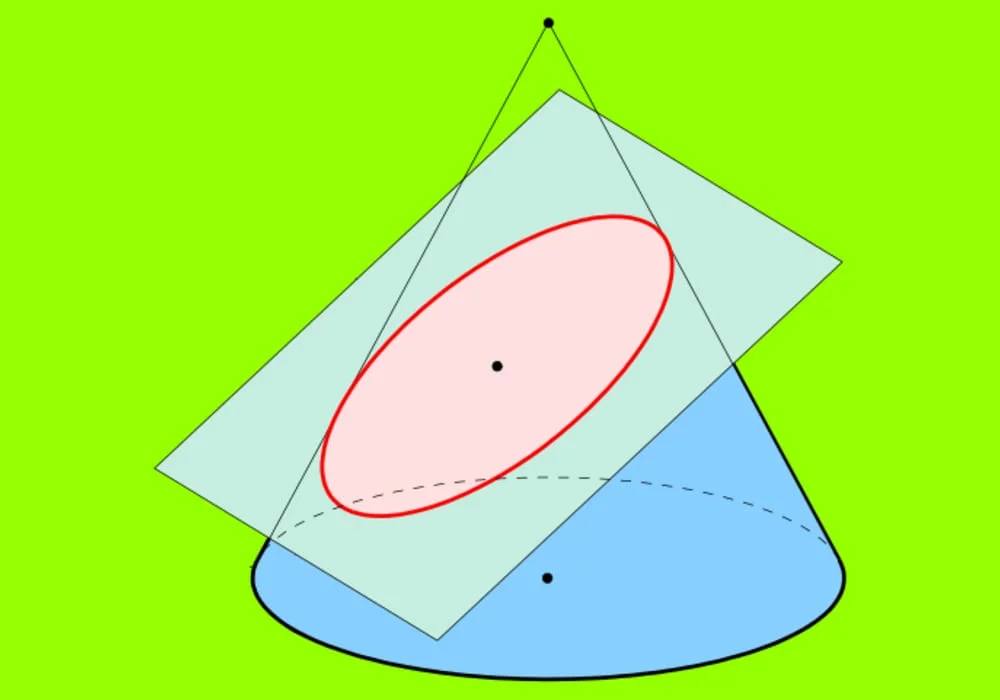
Keliling II (model Ramanujan): $K\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]=\pi \left[3(a+b)-{\sqrt {10ab+3(a^{2}+b^{2})}}\right]$

dan

K\approx \pi \left(a+b\right)\left(1+{\frac {3h}{10+{\sqrt {4-3h}}}}\right)

yang di mana

h={\frac {(a-b)^{2}}{(a+b)^{2}}}

Keliling III (model integral): $K=2\pi a\left[1-\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]$

dan

K=\pi (a+b)\left[1+\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{2^{n}n!}}\right)^{2}{\frac {h^{n}}{(2n-1)^{2}}}\right]

Rumus elips — Elips (merah) diperoleh sebagai persimpangan kerucut dengan bidang miring. Sumber foto: Wikimedia Commons

Persamaan Elips: Vertikal dan horisontal pada titik pusat (0,0)

	Vertikal	Horisontal
	Titik pusat (0,0)
Persamaan	${\frac {x^{2}}{b^{2}}}+{\frac {y^{2}}{a^{2}}}=1$	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$
Panjang sumbu mayor	$2a$	$2a$
Panjang sumbu minor	$2b$	$2b$
Panjang Latus Rectum	$L={\frac {2b^{2}}{a}}$	$L={\frac {2b^{2}}{a}}$
Fokus	$F(0,\pm c)$	$F(\pm c,0)$
Puncak	$P(0,\pm a)$	$P(\pm a,0)$
Direktris	$y=\pm {\frac {a^{2}}{c}}$	$x=\pm {\frac {a^{2}}{c}}$
Eksentrisitas	$e={\frac {c}{a}}$	$e={\frac {c}{a}}$
	Titik pusat (h,k)
Persamaan	${\frac {(x-h)^{2}}{b^{2}}}+{\frac {(y-k)^{2}}{a^{2}}}=1$	${\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1$
Panjang sumbu mayor	$2a$	$2a$
Panjang sumbu minor	$2b$	$2b$
Panjang Latus Rectum	$L={\frac {2b^{2}}{a}}$	$L={\frac {2b^{2}}{a}}$
Fokus	$F(h,k\pm c)$	$F(h\pm c,k)$
Puncak	$P(h,k\pm a)$	$P(h\pm a,k)$
Direktris	$y=\pm {\frac {a^{2}}{c}}$	$x=\pm {\frac {a^{2}}{c}}$
Eksentrisitas	$e={\frac {c}{a}}$	$e={\frac {c}{a}}$

dimana $c={\sqrt {a^{2}-b^{2}}}$

Contoh Soal dan Jawaban Elips atau Oval

1. Tentukanlah titik pusat, jari-jari pendek dan panjang dari persamaan elips 4x² + 9y² +16x – 18y – 11 = 0

Penyelesaian:
4x²+9y²+16x-18y-11=0
4x²+16x+9y²-18y-11=0
4(x²+4x)+9(y²-2y)-11=0
4(x²+4x+4)+9(y²-2y+1)=11+16+9
4(x+2)2+9(y-1)2=36

{ (x+2)² / 9) + (y-1)² / 4) } = 1

Pusat elips (-2,1)
Jari-jari panjang a2 = 9, maka a = √9 = 3
Jari-jari pendek b2 = 4, maka b = √4 = 2

2. Soal certia prosedur medis. Litotripsi merupakan suatu prosedur medis yang dilakukan untuk menghancurkan batu di saluran kemih dengan menggunakan gelombang kejut ultrasonik sehingga pecahannya dapat dengan mudah lolos dari tubuh. Suatu alat yang disebut lithotripter, berbentuk setengah elips 3 dimensi mengaplikasikan sifat-sifat dari titik fokus elips, digunakan untuk mengumpulkan gelombang ultrasonik pada satu titik fokus untuk dikirimkan ke batu ginjal yang terletak di titik fokus lainnya. Jika lithotripter tersebut memiliki panjang (sumbu semi mayor) 16 cm dan berjari-jari (sumbu semi minor) 10 cm, seberapa jauh dari titik puncak seharusnya batu ginjal tersebut diposisikan agar diperoleh hasil yang maksimal?

Jawaban:

Pembahasan Dari soal, kita dapatkan panjang sumbu semi mayornya adalah q = 16, sehingga q² = 16² = 256 dan panjang sumbu semi minornya adalah p = 10, sehingga p² = 10² = 100. Dengan menggunakan persamaan fokus,

ƒ² = |p² = q²|
= |100 – 256|
= 156
ƒ ≈ 12,49 atau ƒ ≈ -12,49

Sehingga, jarak titik puncak dengan titik fokus di mana batu ginjal diposisikan dapat ditentukan sebagai berikut.

d = q + ƒ = 16 + 12,49 = 28,49

Jadi, agar diperoleh hasil yang maksimal, batu ginjal tersebut seharusnya terletak pada jarak 28,49 dari titik puncak lithotripter.

3. Jika diketahui persamaan Elips 4×2 + 9y2 – 48x + 72y +144 = 0. Tentukanlah:
a) Koordinat pusat
b) Koordinat puncak
c) Koordinat focus

Pembahasan :

          4×2 + 9y2 – 48x + 72y +144 = 0
=                   4 (x2 – 12x) + 9 (y2 + 8y) = -144
= 4 (x2 – 12x + 36) + 9 (y2 + 8y +16) = -144 + 144 +144
=                           4 (x – 6)2 + 9 (y + 4)2 = 144
=                                  (x – 6)2 + (y + 4)2 = 1
36              16

a = 6, b = 4, c = √36 – 16 = √20 = 2√5, p = 6, dan q = -4

a) Koordinat pusat (p , q) = (6 , -4)

b) Koordinat puncak :
(p + a , q) = (12 , -4) ; (p – a ,q) = (0, -4) ;
(p , q + b) = (6 , 0) ; dan (p , q – b) = (6 , -8)

c) Koordinat Fokus

F1 (p + c , q) = (6 + 2 √5 , -4)
F2 (p – c , q) = (6 – 2 √5 , -4)

4. Soal cerita permasalahan karakteristik elips. Di Washington D.C., terdapat taman Ellipse yang terletak di antara Gedung Putih dan Monumen Washington. Taman tersebut dikelilingi oleh suatu jalan yang berbentuk elips dengan panjang sumbu mayor dan minornya secara berturut-turut adalah 458 meter dan 390 meter. Apabila pengelola taman tersebut ingin membangun air mancur pada masing-masing fokus taman tersebut, tentukan jarak antara air mancur tersebut!

Jawaban:

Pembahasan Karena panjang dari sumbu mayornya 2p = 458 maka kita peroleh p = 458/2 = 229 dan p² = 229² = 52.441. Sedangkan panjang sumbu minornya 2q = 390, sehingga q = 390/2 = 195 dan q² = 195² = 38.025. Untuk menentukan f, kita dapat menggunakan persamaan fokus.

ƒ² = |p² = q²|
= |52 441 – 38 025|
= 14 416
ƒ ≈ 120 atau ƒ ≈ -120

Jadi, jarak antara kedua air mancur tersebut adalah 2(120) = 240 meter.

5. Diketahui suatu elips dengan pusat O (0, 0), salah satu fokusnya terdapat pada (0, 3), dan Panjang sumbu mayornya adalah 10. Tentukan persamaan elips tersebut!

Pusat (0, 0). Fokus (0, 3) à c = 3.

Panjang sumbu mayor 2a = 10 à a = 5

a² = 25
b² = a²– c² à b² = 25 – 9 = 16.

Persamaan elips: x²/16 + y²/25 = 1

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math is Fun, Wolfram, Math Open Reference

Rumus Elips – Matematika Geometri – Contoh Soal dan Jawaban

Rumus Elips atau Oval

Rumus luas elips

Rumus keliling elips

Keliling I

Keliling II (model Ramanujan)

Keliling III (model integral)

Persamaan Elips: Vertikal dan horisontal pada titik pusat (0,0)

Contoh Soal dan Jawaban Elips atau Oval

1. Tentukanlah titik pusat, jari-jari pendek dan panjang dari persamaan elips 4x² + 9y² +16x – 18y – 11 = 0

3. Jika diketahui persamaan Elips 4×2 + 9y2 – 48x + 72y +144 = 0. Tentukanlah:
a) Koordinat pusat
b) Koordinat puncak
c) Koordinat focus

5. Diketahui suatu elips dengan pusat O (0, 0), salah satu fokusnya terdapat pada (0, 3), dan Panjang sumbu mayornya adalah 10. Tentukan persamaan elips tersebut!

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

Rumus Elips – Matematika Geometri – Contoh Soal dan Jawaban

Rumus Elips atau Oval

Rumus luas elips

Rumus keliling elips

Keliling I

Keliling II (model Ramanujan)

Keliling III (model integral)

Persamaan Elips: Vertikal dan horisontal pada titik pusat (0,0)

Contoh Soal dan Jawaban Elips atau Oval

1. Tentukanlah titik pusat, jari-jari pendek dan panjang dari persamaan elips 4x2 + 9y2 +16x – 18y – 11 = 0

3. Jika diketahui persamaan Elips 4×2 + 9y2 – 48x + 72y +144 = 0. Tentukanlah: a) Koordinat pusat b) Koordinat puncak c) Koordinat focus

5. Diketahui suatu elips dengan pusat O (0, 0), salah satu fokusnya terdapat pada (0, 3), dan Panjang sumbu mayornya adalah 10. Tentukan persamaan elips tersebut!

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

1. Tentukanlah titik pusat, jari-jari pendek dan panjang dari persamaan elips 4x² + 9y² +16x – 18y – 11 = 0

3. Jika diketahui persamaan Elips 4×2 + 9y2 – 48x + 72y +144 = 0. Tentukanlah:
a) Koordinat pusat
b) Koordinat puncak
c) Koordinat focus