Persamaan Kuadrat

Persamaan kuadrat adalah suatu persamaan polinomial berorde dua.

Rumus persamaan kuadrat

Bentuk umum dari persamaan kuadrat adalah

$y=ax^{2}+bx+c\,\!$

dengan

$a\neq 0\,\!$

Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari $x^{2}$ , koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.

Di bawah ini terdapat beberapa jenis persamaan kuadrat secara umum, yaitu:

Akar Real
Akar Imajiner / tidak real ( D < 0 )
Akar Rasional ( D = k² )

Arti nilai a, b dan c

Variasi nilai a

Variasi nilai b

Variasi nilai c

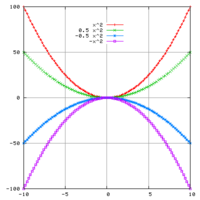
Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.

a menentukan seberapa cekung/cembung parabola yang dibentuk oleh fungsi kuadrat. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a < 0 akan menyebabkan parabola terbuka ke bawah.
b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepatnya adalah -b/2a.
c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0.

Ilustrasi grafik-grafik persamaan kuadrat dengan berbagai variasi nilai a. b dan c dapat dilihat pada gambar di atas.

Gambar diatas menunjukkan lintasan si penerjun yang merupakan merupakan lintasan parabola karena perpindahan horizontal adalah fungsi linear waktu $x=v_x t$ , sementara perpindahan vertikal adalah fungsi kuadrat waktu $y=\tfrac{1}{2} at^2+v_y t+h$ . Akibatnya, jalur mengikuti persamaan kuadrat $y=\tfrac{a}{2v_x^2} x^2+\tfrac{v_y}{v_x} x+h$ , di mana $v_x$ dan $v_y$ adalah komponen horisontal dan vertikal dari kecepatan asli, a adalah percepatan gravitasi dan h adalah tinggi asli. Nilai a harus dianggap negatif di sini, karena arahnya (ke bawah) berlawanan dengan pengukuran tinggi (ke atas).

Rumus Kuadratis (Rumus abc)

y = 0.75 (x + 3.333) (x – 6-000)

Rumus kuadratis dikenal pula dengan nama rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c suatu persamaan kuadrat.

Rumus kuadratis memiliki bentuk

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa

$y=0\,\!$ .

Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk

$y=ax^{2}+bx+c\,\!$

dapat dituliskan menjadi

$y=a(x-x_{1})(x-x_{2})\,\!$ .

Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu

$x_{1}+x_{2}=-{\frac {b}{a}}\,\!$

dan

$x_{1}\cdot x_{2}={\frac {c}{a}}\,\!$ .

Pembuktian Rumus Persamaan Kuadrat

Dari bentuk umum persamaan kuadrat,

ax^{2}+bx+c=0\,\!

bagi kedua ruas untuk mendapatkan $a=1$

x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0,\,\!

Pindahkan ${\frac {c}{a}}$ ke ruas kanan

x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}\,\!

sehingga teknik melengkapkan kuadrat bisa digunakan di ruas kiri.

\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}}{4a^{2}}}=-{\frac {c}{a}}\,\!

Pindahkan $-{\frac {b^{2}}{4ac}}$ ke ruas kanan

\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}\,\!

kemudian samakan penyebut di ruas kanan.

\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}\,\!

Kedua ruas diakar (dipangkatkan setengah), sehingga tanda kuadrat di ruas kiri hilang, dan muncul tanda plus-minus di ruas kanan.

x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}

Pindahkan $-{\frac {b}{2a}}$ ke ruas kanan

x=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}

sehingga didapat rumus kuadrat

x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}

atau

x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}

Diskriminan/determinan

Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar:

b^{2}-4ac,\,\!

yang disebut sebagai diskriminan atau juga sering disebut determinan suatu persamaan kuadrat. Kadang dinotasikan dengan huruf D.

Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks.

Dalam hal ini diskriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat 3 kasus yang mungkin:

Jika diskriminan bersifat positif, akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional — sebaliknya dapat pula merupakan bilangan irrasional kuadrat.

Jika diskriminan bernilai nol, terdapat eksak satu akar, dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar ganda, di mana nilainya adalah:

x=-{\frac {b}{2a}}.\,\!

Jika diskriminan bernilai negatif, tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:

x_{+}={\frac {-b}{2a}}+i\left({\frac {\sqrt {4ac-b^{2}}}{2a}}\right)

dan

x_{-}={\frac {-b}{2a}}-i\left({\frac {\sqrt {4ac-b^{2}}}{2a}}\right)

Jadi akar-akar akan berbeda, jika dan hanya jika diskriminan bernilai tidak sama dengan nol, dan akar-akar akan bersifat riil, jika dan hanya jika diskriminan bernilai tidak negatif.

Akar riil dan kompleks

Persamaan kuadrat dapat memiliki sebuah akar (akar ganda) atau dua buah akar yang berbeda, yang terakhir ini dapat bersifat riil atau kompleks bergantung dari nilai diskriminannya.

Akar-akarnya dapat pula dipandang sebagai titik potongnya dengan sumbu x atau garis y = 0.

Nilai-nilai y

Akar-akar suatu persamaan kuadrat menentukan rentang x di mana nilai-nilai y berharga positif atau negatif. Harga-harga ini ditentukan oleh nilai konstanta kuadrat a:

**Harga-harga y**
	${\displaystyle a><noscript><img decoding=$
	$x<x_{1}\!$	$x_{1}<x<x_{2}\!$	${\displaystyle x><noscript><img decoding=$	$x_{1}<x<x_{2}\!$	${\displaystyle x><noscript><img decoding=$	${\displaystyle y><noscript><img decoding=$	${\displaystyle y><noscript><img decoding=$
$D=0\!$	${\displaystyle y><noscript><img decoding=$	${\displaystyle y><noscript><img decoding=$	$-\!$	$y<0\!$
$D<0\!$	${\displaystyle y><noscript><img decoding=$	${\displaystyle y><noscript><img decoding=$	$-\!$	$y<0\!$

dengan $x_{1}<x_{2}\!$ merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila $x,x_{1},x_{2}\!$ bersifat kompleks, maka yang dimaksud adalah $\Re \ x$ (nilai riil)-nya.

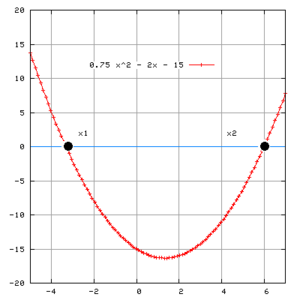
Titik potong dengan garis y = d

Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadrat ( $y_{1}=ax^{2}+bx+c\!$ ) dengan suatu garis mendatar ( $y_{2}=d\!$ ). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.

Intepretasi yang sama pun berlaku, jika:

diskriminan positif, terdapat dua titik potong antara $y_{1}\!$ dan $y_{2}\!$ ,
diskriminan nol, terdapat hanya satu titik potong antara $y_{1}\!$ dan $y_{2}\!$ , dan
diskriminan negatif, tidak terdapat titik potong antara kedua kurva, $y_{1}\!$ dan $y_{2}\!$ .

Geometri

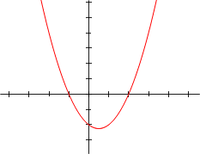
Untuk fungsi kuadrat:
f(x) = x² − x − 2 = (x + 1)(x − 2), dengan variabel x adalah bilangan riil. koordinat-x dari titik-titik di mana kurva menyentuh sumbu-x, x = −1 dan x = 2, adalah akar-akar dari persamaan kuadrat : x² − x − 2 = 0.

Akar-akar dari persamaan kuadrat adalah juga pembuat nol dari fungsi kuadrat tersebut:

f(x)=ax^{2}+bx+c,\,

dikarenakan akar-akar tersebut merupakan nilai $x\,\!$ yang memberikan

f(x)=0.\,

Jika a, b, dan c adalah bilangan riil, dan domain dari $f\,\!$ adalah himpunan bilangan riil, maka pembuat nol dari $f\,\!$ adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.

Mengikuti pernyataan di atas, bahwa jika diskriminan berharga positif, kurva persamaan kuadrat akan menyentuh sumbu-x pada dua buah titik (dua buah titik potong), jika berharga nol, akan menyentuh di satu titik dan jika berharga negatif, kurva tidak akan menyentuh sumbu-x.

Rumus Fungsi Kuadrat

Persamaan fungsi kuadrat : $f(x)=ax^{2}+bx+c\,$ dimana f(x) = y maka titik balik (titik puncak) fungsi kuadrat adalah ( $-{\frac {b}{2a}}\,$ , $-{\frac {D}{4a}}\,$ ).

Pembuktian

Dari bentuk umum persamaan kuadrat,

ax^{2}+bx+c=y\!

a(x^{2}+{\frac {b}{a}}x+{\frac {c}{a}})=y\!

a(\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}}{4a^{2}}}+{\frac {c}{a}})=y\!

anggapan bahwa $(x+{\frac {b}{2a}})^{2}$ adalah 0 maka:

(x+{\frac {b}{2a}})^{2}=0

x=-{\frac {b}{2a}}

a(-{\frac {b^{2}}{4a^{2}}}+{\frac {c}{a}})=y\!

a(-{\frac {b^{2}}{4a^{2}}}+{\frac {4ac}{a^{2}}})=y\!

-{\frac {b^{2}-4ac}{4a}}=y\!

atau

-{\frac {D}{4a}}=y\!

maka titik balik adalah ( $-{\frac {b}{2a}}\,$ , $-{\frac {D}{4a}}\,$ ).

Jenis Jenis Persamaan Kuadrat

Tidak hanya itu saja, akan tetapi persamaan kuadarat juga memiliki beberapa jenis jenis, yaitu seperti di bawah ini :

Akar akar persamaan kuadrat sangat ditentukan ari nilai diskriminan ( D = b² – 4ac ) yang membuat beda jenis akar akar persamaan kuadrat menjadi 3 jenis yaitu :

Apabila D > 0, jadi persamaan kuadrat mempunyai dua akar real yang berlainan.

- Apabila D memiliki bentuk kuadrat sempurna, jadi kedua akarnya rasional.
- Apabila D tidak memiliki bentuk kuadrat sempurna, jadi kedua akarnya irasional.

Apabila D = 0, jadi persamaan kuadrat memiliki dua akar yang sama ( akar kembar ), real, dsan rasional.
Apabila D < 0, jadi persamaan kuadrat tidak memiiki akar real atu kedua akarnya tidak real ( imajiner ).
Bentuk perluasan untuk akar akar real:
- Kedua akar posisitif
D 0
x₁ + x₂ >< 0
x₁ x₂ > 0
- Kedua akar negative
D 0
x₁ + x₂ < 0
x₁ x₂ > 0
- Kedua akar berlainan tanda
D > 0
x₁ x₂ < 0
- Kedua akar bertanda sama
D 0
x₁ x₂ > 0
- Kedua akar saling berlawanan
D > 0
x₁ + x₂ = 0 ( b = 0 )
x₁ x₂ < 0
- Kedua akar saling berkebalikan
D > 0
x₁ + x₂ = 1 ( c = a )

Rumus Persamaan Kuadrat Baru

Nah lalu apa itu persamaan kuadrat baru? Nah jadi seperti yang sudah dijelaskan di atas tadi, persamaan kuadrat bisa dicari akar akarnya dengan memakai metode pemfaktoran, melengkapkan kuadrat sempurna, dan dengan memakai rumus persamaan kuadrat. Kemudian bagaimana jika masalahnya di balik?

Diketahui akar akar persamaan kuadrat dan diminta untuk mentukan persamaan kuadrat yang akar akarnya sudah diketahui itu. Bagaimana juga menentukan persamaan kuadrat barus yang akar akarnya adalah akar akar suatu persamaan kuadrat yang sudah dimodifikasi, nah langsung saja kepembahasannya.

Persamaan kuadrat yang sudah diketahui akar akarnya x₁ dan x₂ bisa disusun kedalam dua bentuk yaitu:

( x – x₁ ) ( x – x₂ ) = 0

Atau

x² – ( x₁ + x₂ ) x + ( x₁ ) ( x₂ ) = 0

Nah bagaimana dengan persamaan grafik fungsi kuadrat, jika bentuk umum fungsi kuadrat itu adalah f ( x ) = ax² + bx + c = 0 yang amana a, b, dan c merupakan bilangan real dan a 0. Nah sedangkan grafik fungsi ini memiliki gambar yang bentuknya parabola.

Untuk menggambarkan “Rumus Persamaan Kuadrat Baru” dibutuhkan langkah langkah seperti di bawah ini:

Menentukan titik potong dengan sumbu x, syaratnya yaitu y = 0 jadi ax² + bx + c = 0,

( x – x₁ ) ( x – x₂ ) = 0, titiknya ( x₁, 0 ) dan ( x₂, 0 )

Menentukan titik potong dengan sumbu y, memiliki syarat yaitu x = 0 jadi

y = a ( 0 )² + b( 0 ) + c = c titiknya ( 0, c )

Menentukan persamaan sumbu simetri, yaitu : x = , xp merupakan titik tengah x₁ dan x₂. jadi persamaan sumbu simetri yaitu :

Menentukan nilai ekstrim atau nilai maksimum atau minimum fungsi, yaitu = ² + b + c, jadi nilai maksimum atau minimum fungsi adlaah

Catatan apabila a > 0 jadi nilai minimum dan jika a < 0 jadi nilai maksimum

Menentukan titik balik fungsi maksimum atau minim.
Menggambar fungsi.

Macam – Macam Akar Persamaan Kuadrat

Untuk mengetahui berbagai macam dari akar persamaan kuadrat, kita juga bisa mengetahuinya dengan memakai rumus D = b2 – 4ac.

Apabila terbentuk nilai D maka kita akan dengan mudah dapat menemukan berbagai akarnya.

Berikut ini adalah beberapa jenis dari persamaan kuadrat secara umum, antara lain:

1. Akar Real ( D ≥ 0 )

Akar real berlainan jika diketahui= D > 0

2. Akar Imajiner/ Tidak Real ( D < 0 )

3. Akar Rasional ( D = k²)

Contoh Soal dan Jawaban Persamaan Kuadrat

1. Sebuah grafik fungsi kuadrat memotong sumbu –x di A ( 1, 0 ) dan B ( 2, 0 ). Jika grafik tersebut juga melewati titik ( 0, 4 ), maka tentukanlah persamaan fungsi kuadratnya!

Penyelesaian :

Persamaan fungsi kuadrat bisa dinyatakan menjadi y = a ( x – 1 )

( x – 2 ). Nilai a ditentukan dari keterangan bahwa fungsi kuadrat itu lewat titik ( 0, 4 ). Maka artinya untuk nilai x = 0 didapatkan y = 4.

y = a ( x – 1 ) ( x – 2 )
4 = a ( 0 – 1 ) ( 0 – 2 )
4 = a ( -1 ) ( -2 )
4 = 2a
a = 2

Maka dari itu, persamaan fungsi kuadratnya adalah seperti di bawah ini:

y = f ( x )
y = a ( x – 1 ) ( x – 2 )
y = 2 ( x – 1 ) ( x – 2 )
y = 2 ( x² – x – 2x + 2 )
y = 2 ( x² – 3x + 2 ?)
y = 2x² – 6x + 4

2. Jika bentuk umum dari persamaan x² – 4 = 3 ( x – 2 ) yaitu ax² + bx + c = 0, jadi nilai a, b, dan c berturut turut adalah…

Penyelesaian :

Untuk menentukan nilai a, b, dan c harus mengubah bentuk soal menjadi bentuk umum terlebih dahulu yaitu sebagai berikut :

x² – 4 = 3 ( x – 2)
x² – 4 = 3x – 6
x² – 4 – 3x + 6 = 0
x² – 3x + 2 = 0
a = 1, b = -3, dan c = 2

Jadi, nilai a, b, dan c adalah 1, -3, dan -2.

3. Soal Menyusun Persamaan Kuadrat. Persamaan kuadrat yang akar-akarnya -2 serta 3 yaitu…

A. x² – 2x – 6 = 0
B. x² – x + 6 = 0
C. x² – x – 6 = 0
D. x² + x – 6 = 0

Jawaban:

Persamaan kuadratnya ialah:

⇒ (x – x₁)(x – x₂) = 0
⇒ (x – (-2))(x – 3) = 0
⇒ (x + 2)(x – 3) = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x² – x – 6 = 0

Jawaban: C.

4. Apabila bentuk umum dari persamaan x² – 4 = 3 ( x – 2 ) yaitu ax² + bx + c = 0, jadi nilai a, b, dan c berturut turut adalah …

Penyelesaian :

Untuk menentukan nilai a, b, dan c harus mengubah bentuk soal menjadi bentuk umum terlebih dahulu yaitu sebagai berikut :

x² – 4 = 3 ( x – 2)
x² – 4 = 3x – 6
x² – 4 – 3x + 6 = 0
x² – 3x + 2 = 0
a = 1, b = -3, dan c = 2.

5. Soal Menentukan Akar Persamaan Kuadrat. Apabila salah satu akar dari persamaan kuadrat x² + 2x + c = 0 yaitu 3, maka akar lainnya adalah…

A. x = 5
B. x = 3
C. x = -5
D. x = -15

Jawaban:

Langkah pertama yang harus kita lakukan adalah mensubstitusikan nilai x = 3 untuk mengetahui nilai c:

⇒ x² + 2x + c = 0
⇒ 3² + 2(3) + c = 0
⇒ 9 + 6 + c = 0
⇒ 15 + c = 0
⇒ c = -15

Langkah kedua yang harus kita lakukan adalah mensubstitusikan nilai c sehingga persamaanya menjadi:

⇒ x² + 2x + c = 0
⇒ x² + 2x – 15 = 0

Kemudia menentukan nilai akarnya dengan pemfaktoran:

⇒ (x + 5)(x – 3) = 0
⇒ x = -5 atau x = 3

Jawaban: C.

6. Apabila terdapat salah satu akar dari persamaan kuadarat x² – 4x + c = 0 adalah 2m, jadi nilai c yang memenuhi persamaan itu adalah …

Penyelesaian :

Langkah pertama yaitu harus substitusikan nilai x = 2 ke persamaannya :

x² – 4x + c = 0
2² – 4 ( 2 ) + c = 0
4 – 8 + c = 0
-4 + c = 0
C = 4.

7. Apabila salah sau akar dari persamaan kuadrat x² + 2x + c = 0 yaitu 3, jadi berapa akar lainnya ?

Penyelesaian :

Substitusikan nilai x = 3 untuk tahu nilai c :

x² + 2x + c = 0
3² + 2 ( 3 ) + c = 0
9 + 6 + c = 0
15 + c = 0
C = -15

Substiusi nilai c jadi persamaannya menjadi :

x² + 2x + c = 0
x² + 2x – 15 = 0

kemudian tetukannlah akar dengan pemfaktorannya :

( x + 5 ) ( x – 3 ) = 0
X = -5 atau x = 3

8. Soal Menentukan Jenis Akar Persamaan Kuadrat. Jenis akar-akar dari persamaan x² – 4x + 4 = 0 yaitu…

A. Real kembar
B. Real berbeda
C. Imajiner
D. Real berlawanan tanda

Jawaban:

Berdasarkan dari nilai akarnya, kita memakai cara pemfaktoran, yaitu:

⇒ x² – 4x + 4 = 0
⇒ (x – 2)(x – 2) = 0
⇒ x = 2 atau x = 2

Yang artinya, akarnya real kembar.

Metode kedua adalah:

Tinjau nilai diskriminannya, maka:

⇒ D = b² – 4ac
⇒ D = (-4)² – 4(1)(4)
⇒ D = 16 – 16
⇒ D = 0

Untuk D = 0, akarnya ialah real kembar.

Jawaban: A.

9. Dalam waktu x jam, kendaraan yang berjalan dengan kecepatan rata-rata (x+15) km/jam dapat menempuh jarak 100 km.
a. Bentuklah persamaan kuadrat dalam bentuk x!
b. Selesaikan persamaan kuadrat tersebut!

Jawaban:

a. x(x+15)=100

b. x²+15=100x²+15-100=0(x+20)(x-5)=0x+20=0
x₁=-20
x-5=0
x₂=5
x= 5 jam

Kita harus memakai x₂ karena bilangan tersebut adalah bilangan bulat positif, waktu tidak pernah menggunakan bilangan negatif.

10. Diskriminan D>0. Persamaan kuadrat dengan nilai diskriminan D>0 mempunyai dua akar real yang berlainan. Akar-akarnya bisa berupa bilangan bulat, bilangan pecahan, dan bilangan akar.

Jika koefisien b=0, maka persamaan kuadrat ini juga mempunyai akar-akar real berkebalikan/berlawanan.

Contoh:

Koefisien a<1

$\vspace{1pc}-4x^2+10x-5=0\\ \vspace{1pc}a=-4\;b=10\;c=-5\\ \vspace{1pc}x_{1,2}=\frac{-b\pm\sqrt{b^2-(4.a.c)}}{2a}\\ \vspace{1pc}x_{1,2}=\frac{-10\pm\sqrt{10^2-(4.(-4).(-5))}}{2(-4)}\\ \vspace{1pc}x_{1,2}=\frac{-10\pm\sqrt{100-80}}{-8}\\ \vspace{1pc}x_{1,2}=\frac{-10\pm\sqrt{20}}{-8}\\ \vspace{1pc}x_{1,2}=\frac{-10\pm2\sqrt{5}}{-8}\\ \vspace{1pc}x_{1}=\frac{-10+2\sqrt{5}}{-8}=\frac{-10}{-8}+\frac{2}{-8}\sqrt{5}=\frac{5}{4}-\frac{1}{4}\sqrt{5}\\ \vspace{1pc}x_{2}=\frac{-10-2\sqrt{5}}{-8}=\frac{-10}{-8}-\frac{2}{-8}\sqrt{5}=\frac{5}{4}+\frac{1}{4}\sqrt{5}$

Koefisien a=1

$\vspace{1pc}x^2-3x-4=0\\ \vspace{1pc}a=1\;b=-3\;c=-4\\ \vspace{1pc}x_{1,2}=\frac{-b\pm\sqrt{b^2-(4.a.c)}}{2a}\\ \vspace{1pc}x_{1,2}=\frac{-(-3)\pm\sqrt{(-3)^2-(4.1.(-4))}}{2(1)}\\ \vspace{1pc}x_{1,2}=\frac{3\pm\sqrt{9-(-16)}}{2}\\ \vspace{1pc}x_{1,2}=\frac{3\pm\sqrt{25}}{2}\\ \vspace{1pc}x_{1,2}=\frac{3\pm 5}{2}\\ \vspace{1pc}x_{1}=\frac{3+5}{2}=4\\ \vspace{1pc}x_{2}=\frac{3-5}{2}=-1$

Koefisien a>1

$\vspace{1pc}4x^2-9=0\\ \vspace{1pc}a=4\;b=0\;c=-9\\ \vspace{1pc}x_{1,2}=\frac{-b\pm\sqrt{b^2-(4.a.c)}}{2a}\\ \vspace{1pc}x_{1,2}=\frac{-0\pm\sqrt{0^2-(4.4.(-9))}}{2(4)}\\ \vspace{1pc}x_{1,2}=\frac{0\pm\sqrt{0-(-144)}}{8}\\ \vspace{1pc}x_{1,2}=\frac{0\pm\sqrt{144}}{8}\\ \vspace{1pc}x_{1,2}=\frac{0\pm 12}{8}\\ \vspace{1pc}x_{1}=\frac{0+12}{8}=\frac{3}{2}=1\frac{1}{2}\\ \vspace{1pc}x_{2}=\frac{0-12}{8}=-\frac{3}{2}=-1\frac{1}{2}$

11. Tentukan jenis akar dari persamaan di bawah ini: x2 + 4x + 2 = 0 !

Jawaban:

Dari persamaan = x2 + 4x + 2 = 0, maka dapat kita ketahui:

Diketahui:

a = 1
b = 4
c = 2

Penyelesaian:

D = b2 – 4ac
D = 42 – 4(1)(2)
D = 16 – 8
D = 8 ( D>8, maka akarnya pun adalah akar real namun berbeda )

»Akar real sama x1 = x2 jika diketahui D = 0

12. Buktikan jika persamaan di bawah ini mempunyai akar real kembar: 2×2 + 4x + 2 = 0

Jawaban:

Dari persamaan tersebut yaitu: = 2×2 + 4x + 2 = 0, maka

Diketahui:

a = 2
b = 4
c = 2

Penyelesaian:

D = b2 – 4ac
D = 42 – 4(2)(2)
D = 16 – 16
D = 0 ( D=0, terbukti jika akar real dan kembar)

13. Tentukanlah jenis akar dari persamaan di bawah ini: x2 + 2x + 4 = 0 !

Jawaban:

Dari persamaan tersebut yakni: = x2 + 2x + 4 = 0, maka

Diketahui:

a = 1
b = 2
c = 4

Penyelesaian:

D = b2 – 4ac
D = 22 – 4(1)(4)
D = 4 – 16
D = -12 (D<0, sehingga akar-akarnya merupakan akar tidak real)

14. Soal Jumlah Akar-akar Persamaan Kuadrat. Apabila akar-akar persamaan x² – 3x – 10 = 0 ialah x₁ dan x₂, maka hasil dari x₁ + x₂ sama dengan…

A. x₁ + x₂ = 3
B. x₁ + x₂ = 4
C. x₁ + x₂ = 5
D. x₁ + x₂ = 7

Jawaban:

Dengan menggunakan cara pemfaktoran, maka:

⇒ x² – 3x – 10 = 0
⇒ (x + 2)(x – 5) = 0
⇒ x₁ = -2 atau x₂ = 5

Jumlah akar-akarnya yaitu:

⇒ x₁ + x₂ = -2 + 5
⇒ x₁ + x₂ = 3

Dengan menggunakan metode cepat, yaitu:

Dari x² – 3x – 10 = 0
Dik : a = 1, b = -3, c = -10

Jumlah akarnya yaitu:

⇒ x₁ + x₂ = -b/a
⇒ x₁ + x₂ = -(-3)/1
⇒ x₁ + x₂ = 3

Jawaban: A.

15. Tentukan jenis akar dari persamaan di bawah ini: x² + 4x + 3 = 0

Jawaban:

Dari persamaan tersebut yakni: = x² + 4x + 3 = 0, maka

Diketahui:

a = 1
b = 4
c = 3

Penyelesaian:

D = b² – 4ac
D = 4² – 4(1)(3)
D = 16 – 12
D = 4 = 2²= k² (Sebab D=k²=4, sehingga akar persamaannya merupakan akar rasional)

16. Selesaikan persamaan kuadrat berikut dengan menggunakan metode faktorisasi 5x²+13x+6=0!

Jawaban:

5x² + 13x = 6 = 0
5x² + 10x + 3x + 6 = 0
5x(x + 2) + 3(x + 2) = 0
(5x + 3)(x + 2) = 0
5x = -3
x = -3/5, atau x = -2

Sehingga, himpunan penyelesaian HP = (-3/5, -2)

17. Tentukan persamaan kuadrat di mana akar akarnya yaitu -2 dan 3.

Jawaban:

x₁=-2 dan x₂=3
(x-(-2))(x-3)=0
(x+2)(x+3)
x²-3x+2x-6=0
x²-x-6=0

18. Tentukan persamaan kuadrat yang akar-akarnya 3 dan juga -1/2!

Jawaban:

x₁=3 dan x₂= -1/2
x₁₊ x₂=3 -1/2 =6/2 – 1/2 = 5/2
x_1.x₂= 3 (-1/2) = -3/2

Sehingga, persamaan kuadratnya yaitu:
x²-( x₁₊ x₂)x+(x_1.x₂)=0
x²– 5/2 x – 3/2=0 (masing-masing ruas dikali 2)
2x²-5x-3=0

19. Soal Bentuk Umum Persamaan Kuadrat. Apabila bentuk umum dari persamaan x² – 4 = 3(x – 2) merupakan ax² + bx + c = 0, maka nilai a, b, dan c berturut-turut adalah…

A. 1, -3, 2
B. 1, -2, 3
C. 1, 3, -2
D. 1, -3, -10

Jawaban:

Untuk menentukan nilai a, b, dan c maka kita harus merubah bentuk soal menjadi bentuk umum terlebih dahulu.

Caranya:

⇒ x² – 4 = 3(x – 2)
⇒ x² – 4 = 3x – 6
⇒ x² – 4 – 3x + 6 = 0
⇒ x² – 3x + 2 = 0
⇒ a = 1, b = -3, dan c = 2

Jawaban: A.

20. Soal Akar Persamaan Kuadrat. Apabila salah satau akar dari persamaan kuadrat x² – 4x + c = 0 yaitu 2, maka nilai c yang memenuhi persamaan itu yakni…

A. c = 2
B. c = 4
C. c = -4
D. c = -6

Jawaban:

Langkah pertama yang harus kita lakukan adalah mensubstitusikan nilai x = 2 ke persamaannya, sehingga:

⇒ x² – 4x + c = 0
⇒ 2² – 4(2) + c = 0
⇒ 4 – 8 + c = 0
⇒ -4 + c = 0
⇒ c = 4

Jawaban: B.

21. Soal Himpunan Penyelesaian Persamaan Kuadrat. Himpunan penyelesaian dari persamaan: x² + 5x + 6 = 0 yaitu…

A. {-2, -3}
B. {-2, 3}
C. {-3, 2}
D. {3, 4}

Jawaban:

Dengan menggunakan cara pemfaktoran, maka:

⇒ x² + 5x + 6 = 0
⇒ (x + 2)(x + 3) = 0
⇒ x = -2 atau x = -3
⇒ HP = {-2, -3}

Jawaban: A.

22. Soal Menentukan Akar Lainnya dari Persamaan Kuadrat. Salah satu akar dari persamaan 3x² – 2x + c = 0 ialah 2, akar lainnya yaitu…

A. -4/5
B. -4/3
C. 3/4
D. 4/3

Jawaban:

Langkah pertama yang harus kita lakukan adalah mensubstitusikan nilai x = 2 ke persamaan:

⇒ 3x² – 2x + c = 0
⇒ 3(2)² – 2(2) + c = 0
⇒ 3.4 – 4 + c = 0
⇒ 12 – 4 + c = 0
⇒ 8 + c = 0
⇒ c = -8

Langkah kedua yang harus kita lakukan adalah mensubstitusikan nilainilai c sehingga persamaannya menjadi:

⇒ 3x² – 2x + c = 0
⇒ 3x² – 2x + (-8) = 0
⇒ 3x² – 2x – 8 = 0

Dengan menggunakan metode pemfaktoran:

⇒ 3x² – 2x – 8 = 0
⇒ (3x + 4)(x – 2) = 0
⇒ x = -4/3 atau x = 2

Sehingga, akar lainnya yaitu -4/3.

Jawaban: B.

23. Soal Menentukan Nilai Koefisien Persamaan Kuadrat. Apabila akar-akar dari persamaan x² + bx + c = 0 yaitu -1 dan 3, maka nilai b yang memenuhi persamaan itu adalah…

A. b = 4
B. b = 2
C. b = -1
D. b = -2

Jawaban:

Langkah pertama yang harus kita lakukan adalah mensubstitusikan nilai x = -1 ke persamaan:

⇒ x² + bx + c = 0
⇒ (-1)² + b(-1) + c = 0
⇒ 1 – b + c = 0
⇒ -b + c = -1
⇒ c = b – 1 …. (1)

Langkah kedua yang harus kita lakukan adalah mensubstitusikan nilai x = 3 ke persamaan:

⇒ x² + bx + c = 0
⇒ (3)² + b(3) + c = 0
⇒ 9 + 3b + c = 0
⇒ 3b + c = -9 …. (2)

Kemudian mensubsitusikan persamaan (1) ke persamaan (2), sehingga:
⇒ 3b + c = -9
⇒ 3b + (b – 1) = -9
⇒ 4b – 1 = -9
⇒ 4b = -9 + 1
⇒ 4b = -8
⇒ b = -2

Jawaban: D.

24. Soal Melengkapi Kuadrat Sempurna. Bentuk kuadrat sempurna dari persamaan x² – 6x – 7 = 0 yaitu…

A. (x + 3)² = 16
B. (x – 3)² = 16
C. (x – 4)² = 16
D. (x – 5)² = 25

Jawaban:

Langkah pertama adalah membentuk kuadrat sempurna dengan cara mengubah bentuk ax² + bx + c = 0 menjadi

x² + b/ax = -c/a.

Bentuk kuadrat sempurnanya yaitu:

⇒ x² – 6x – 7 = 0
⇒ x² – 6/1x = 7/1
⇒ x² – 6x = 7

Kedua adalah semua ruas sama-sama ditambah dengan bilangan yang sama, sehingga:
⇒ x² – 6x + (3)² = 7 + (3)²
⇒ x² – 6x + 9 = 7 + 9
⇒ (x – 3)² = 16

Jawaban: B

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math World, Popular Mechanics, Cliffs Notes

Persamaan Kuadrat – Rumus Kuadratis (Rumus abc), Pembuktian rumus persamaan kuadrat, Diskriminan/determinan, Akar riil dan kompleks, Geometri, Rumus fungsi kuadrat

Persamaan Kuadrat

Rumus persamaan kuadrat

Di bawah ini terdapat beberapa jenis persamaan kuadrat secara umum, yaitu:

Arti nilai a, b dan c

Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.

Rumus Kuadratis (Rumus abc)

Rumus kuadratis memiliki bentuk

Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk

dapat dituliskan menjadi

Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu

Pembuktian Rumus Persamaan Kuadrat

Diskriminan/determinan

Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar:

Dalam hal ini diskriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat 3 kasus yang mungkin:

Akar riil dan kompleks

Nilai-nilai y

Titik potong dengan garis y = d

Intepretasi yang sama pun berlaku, jika:

Geometri

Akar-akar dari persamaan kuadrat adalah juga pembuat nol dari fungsi kuadrat tersebut:

dikarenakan akar-akar tersebut merupakan nilai {\displaystyle x\,\!}<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ec21bb206c6c9f458130ab7ffddfe3fd8d0fa6bb" alt="{\displaystyle x\,\!}" aria-hidden="true"> yang memberikan

Rumus Fungsi Kuadrat

Jenis Jenis Persamaan Kuadrat

Rumus Persamaan Kuadrat Baru

Persamaan kuadrat yang sudah diketahui akar akarnya x₁ dan x₂ bisa disusun kedalam dua bentuk yaitu:

Untuk menggambarkan “Rumus Persamaan Kuadrat Baru” dibutuhkan langkah langkah seperti di bawah ini:

Macam – Macam Akar Persamaan Kuadrat

1. Akar Real ( D ≥ 0 )

2. Akar Imajiner/ Tidak Real ( D < 0 )

3. Akar Rasional ( D = k2 )

Contoh Soal dan Jawaban Persamaan Kuadrat

1. Sebuah grafik fungsi kuadrat memotong sumbu –x di A ( 1, 0 ) dan B ( 2, 0 ). Jika grafik tersebut juga melewati titik ( 0, 4 ), maka tentukanlah persamaan fungsi kuadratnya!

2. Jika bentuk umum dari persamaan x² – 4 = 3 ( x – 2 ) yaitu ax² + bx + c = 0, jadi nilai a, b, dan c berturut turut adalah…

3. Soal Menyusun Persamaan Kuadrat. Persamaan kuadrat yang akar-akarnya -2 serta 3 yaitu…

4. Apabila bentuk umum dari persamaan x² – 4 = 3 ( x – 2 ) yaitu ax² + bx + c = 0, jadi nilai a, b, dan c berturut turut adalah …

5. Soal Menentukan Akar Persamaan Kuadrat. Apabila salah satu akar dari persamaan kuadrat x2 + 2x + c = 0 yaitu 3, maka akar lainnya adalah…

6. Apabila terdapat salah satu akar dari persamaan kuadarat x² – 4x + c = 0 adalah 2m, jadi nilai c yang memenuhi persamaan itu adalah …

7. Apabila salah sau akar dari persamaan kuadrat x² + 2x + c = 0 yaitu 3, jadi berapa akar lainnya ?

8. Soal Menentukan Jenis Akar Persamaan Kuadrat. Jenis akar-akar dari persamaan x2 – 4x + 4 = 0 yaitu…

9. Dalam waktu x jam, kendaraan yang berjalan dengan kecepatan rata-rata (x+15) km/jam dapat menempuh jarak 100 km. a. Bentuklah persamaan kuadrat dalam bentuk x! b. Selesaikan persamaan kuadrat tersebut!

10. Diskriminan D>0. Persamaan kuadrat dengan nilai diskriminan D>0 mempunyai dua akar real yang berlainan. Akar-akarnya bisa berupa bilangan bulat, bilangan pecahan, dan bilangan akar.

11. Tentukan jenis akar dari persamaan di bawah ini: x2 + 4x + 2 = 0 !

12. Buktikan jika persamaan di bawah ini mempunyai akar real kembar: 2×2 + 4x + 2 = 0

13. Tentukanlah jenis akar dari persamaan di bawah ini: x2 + 2x + 4 = 0 !

14. Soal Jumlah Akar-akar Persamaan Kuadrat. Apabila akar-akar persamaan x2 – 3x – 10 = 0 ialah x1 dan x2, maka hasil dari x1 + x2 sama dengan…

15. Tentukan jenis akar dari persamaan di bawah ini: x2 + 4x + 3 = 0

16. Selesaikan persamaan kuadrat berikut dengan menggunakan metode faktorisasi 5x2+13x+6=0!

17. Tentukan persamaan kuadrat di mana akar akarnya yaitu -2 dan 3.

18. Tentukan persamaan kuadrat yang akar-akarnya 3 dan juga -1/2!

19. Soal Bentuk Umum Persamaan Kuadrat. Apabila bentuk umum dari persamaan x2 – 4 = 3(x – 2) merupakan ax2 + bx + c = 0, maka nilai a, b, dan c berturut-turut adalah…

20. Soal Akar Persamaan Kuadrat. Apabila salah satau akar dari persamaan kuadrat x2 – 4x + c = 0 yaitu 2, maka nilai c yang memenuhi persamaan itu yakni…

21. Soal Himpunan Penyelesaian Persamaan Kuadrat. Himpunan penyelesaian dari persamaan: x2 + 5x + 6 = 0 yaitu…

22. Soal Menentukan Akar Lainnya dari Persamaan Kuadrat. Salah satu akar dari persamaan 3x2 – 2x + c = 0 ialah 2, akar lainnya yaitu…

23. Soal Menentukan Nilai Koefisien Persamaan Kuadrat. Apabila akar-akar dari persamaan x2 + bx + c = 0 yaitu -1 dan 3, maka nilai b yang memenuhi persamaan itu adalah…

24. Soal Melengkapi Kuadrat Sempurna. Bentuk kuadrat sempurna dari persamaan x2 – 6x – 7 = 0 yaitu…

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Nilai Pi 1 juta digit pertama | Analisis dan…

Menghitung Dimensi Balok dari Luas Jaring-Jaringnya

Rumus Matematika dan Contoh untuk Penggunaan Sehari-hari

Tinggalkan Balasan Batalkan balasan

dikarenakan akar-akar tersebut merupakan nilai $x\,\!$ yang memberikan

3. Akar Rasional ( D = k²)

5. Soal Menentukan Akar Persamaan Kuadrat. Apabila salah satu akar dari persamaan kuadrat x² + 2x + c = 0 yaitu 3, maka akar lainnya adalah…

8. Soal Menentukan Jenis Akar Persamaan Kuadrat. Jenis akar-akar dari persamaan x² – 4x + 4 = 0 yaitu…

9. Dalam waktu x jam, kendaraan yang berjalan dengan kecepatan rata-rata (x+15) km/jam dapat menempuh jarak 100 km.
a. Bentuklah persamaan kuadrat dalam bentuk x!
b. Selesaikan persamaan kuadrat tersebut!

14. Soal Jumlah Akar-akar Persamaan Kuadrat. Apabila akar-akar persamaan x² – 3x – 10 = 0 ialah x₁ dan x₂, maka hasil dari x₁ + x₂ sama dengan…

15. Tentukan jenis akar dari persamaan di bawah ini: x² + 4x + 3 = 0

16. Selesaikan persamaan kuadrat berikut dengan menggunakan metode faktorisasi 5x²+13x+6=0!

19. Soal Bentuk Umum Persamaan Kuadrat. Apabila bentuk umum dari persamaan x² – 4 = 3(x – 2) merupakan ax² + bx + c = 0, maka nilai a, b, dan c berturut-turut adalah…

20. Soal Akar Persamaan Kuadrat. Apabila salah satau akar dari persamaan kuadrat x² – 4x + c = 0 yaitu 2, maka nilai c yang memenuhi persamaan itu yakni…

21. Soal Himpunan Penyelesaian Persamaan Kuadrat. Himpunan penyelesaian dari persamaan: x² + 5x + 6 = 0 yaitu…

22. Soal Menentukan Akar Lainnya dari Persamaan Kuadrat. Salah satu akar dari persamaan 3x² – 2x + c = 0 ialah 2, akar lainnya yaitu…

23. Soal Menentukan Nilai Koefisien Persamaan Kuadrat. Apabila akar-akar dari persamaan x² + bx + c = 0 yaitu -1 dan 3, maka nilai b yang memenuhi persamaan itu adalah…

24. Soal Melengkapi Kuadrat Sempurna. Bentuk kuadrat sempurna dari persamaan x² – 6x – 7 = 0 yaitu…