Perpindahan Panas
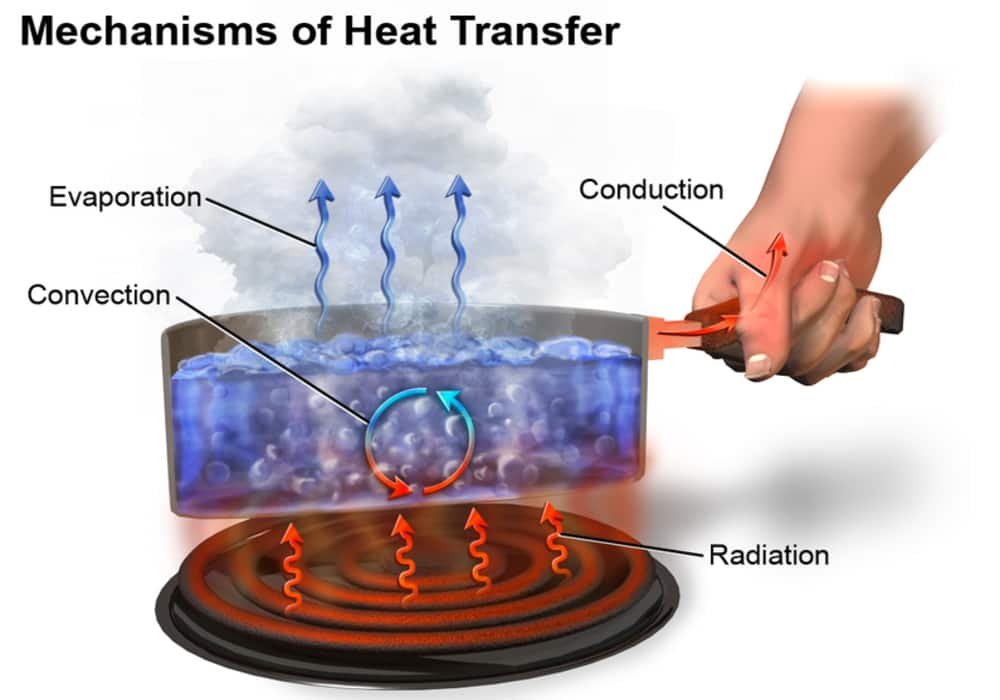
Perpindahan panas adalah salah satu dari displin ilmu teknik termal yang mempelajari cara menghasilkan panas, menggunakan panas, mengubah panas, dan menukarkan panas di antara sistem fisik. Perpindahan panas diklasifikasikan menjadi konduktivitas termal, konveksi termal, radiasi termal, dan perpindahan panas melalui perubahan fasa.
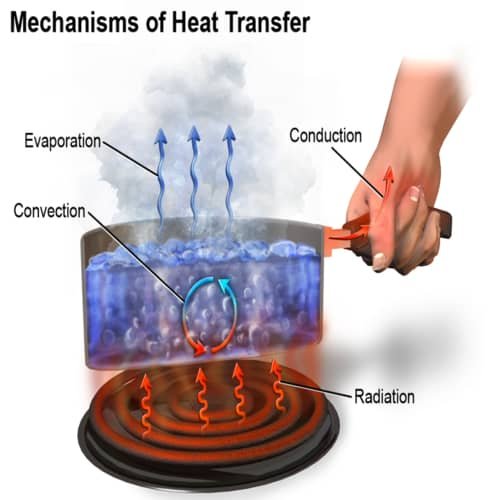
Mekanisme Perpindahan Panas
Bentuk-bentuk dasar perpindahan panas pada massa adalah:
1. Konduksi atau difusi
Perpindahan energi antara objek yang mengalami kontak fisik dengan sumber panas.
Ada beberapa kesamaan pada persamaan perpindahan panas, momentum, dan massa semuanya dapat dipindahkan dengan difusi (atau pembauran adalah peristiwa mengalirnya atau berpindahnya suatu zat dalam pelarut dari bagian berkonsentrasi tinggi ke bagian yang berkonsentrasi rendah):
- Massa: tersebarnya bau di udara merupakan contoh difusi massa.
- Panas: konduksi panas pada material padat merupakan contoh difusi panas.
- Momentum: drag yang dialami oleh tetesan air hujan di atmosfer merupakan contoh difusi momentum.
Berdasarkan daya hantar kalor, benda dibedakan menjadi dua jenis yaitu konduktor dan isolator.
- Konduktor adalah benda/ bahan yang dapat mengantarkan kalor dengan baik. Konduktor dapat dimanfaatkan pada alat masak dari logam, raksa pada thermometer, tabung tembaga pada radioator mobil. Contoh konduktor adalah besi, tembaga, aluminium, silicon, dan perak.
- Isolator adalah benda yang tidak dapat menghantarkan panas. Isolator dapat dimanfaatkan untuk pakaian dengan berbahan wol saat musim dingin, peralatan rumah tangga, dan digunakan oleh orang eskimo dalam membuat iglo. Contoh dari isolator adalah kayu, kaca, kertas, plastik.
Persamaan perpindahan molekuler untuk momentum Hukum Newton, panas Hukum Fourier, dan massa Hukum Fick sangat mirip.
| Besaran yang berpindah | Fenomena fisika | Persamaan |
|---|---|---|
| Momentum | Viskositas (Fluida Newtonian) | |
| Energi | Konduksi panas (Hukum Fourier) | |
| Massa | Difusi molekuler (Hukum Fick) |
Perpindahan Momentum
Pada perpindahan momentum transfer, fluida dibayangkan sebagai objek yang terdistribusi kontinu. Studi mengenai perpindahan momentum atau mekanika fluida dapat dibedakan menjadi 2 cabang: statika fluida (fluida diam) dan dinamika fluida (fluida bergerak). Ketika fluida bergerak pada arah x paralel dengan permukaan solid, fluida tersebut memiliki momentum pada arah-x dengan konsentrasi υxρ. Dengan difusi acak molekul maka ada perpindahan molekul pada arah-z. Maka momentum pada arah-x berpindah ke arah-z dari lapisan yang bergerak lebih cepat ke lapisan yang bergerak lebih lambat. Persamaan perpindahan momentum menurut Hukum Newton tentang Viskositas dapat ditulis sebagai berikut:
dengan τzx adalah fluks momentum arah-x pada arah-z, ν is μ/ρ, difusivitas momentum z adalah jarak transport atau difusi, ρ adalah densitas, dan μ adalah viskositas.
Perpindahan massa
Ketika sistem berisi 2 atau lebih komponen yang konsentrasinya berbeda-beda antar titik, ada kecenderungan alami dari massa untuk berpindah, untuk meminimalkan perbedaan konsentrasi dalam sistem.
Perpindahan massa dalam sistem dijelaskan oleh Hukum pertama Fick: ‘Difusi fluks dari konsentrasi tinggi ke konsentrasi rendah berbanding lurus dengan gradien konsentrasi substansi dan difusivitas substansi pada medium.’ Perpindahan massa dapat berlangsung karena ada perbedaan driving force. Beberapa diantaranya adalah:
- Massa dapat berpindah akibat gradien tekanan (difusi tekanan)
- Difusi gata muncul akibat gerak beberapa gaya luar
- Difusi disebabkan oleh gradien temperatur (difusi termal)
Dapat dibandingkan dengan Hukum Fourier mengenai konduksi panas:
dengan D adalah konstanta difusivitas.
Perpidahan panas
Prinsip dasar perpindahan panas mengikuti hukum pertama termodinamika yang dapat dinyatakan sebagai berikut:
Untuk sistem lain yang alirannya turbulen, geometri kompleks atau boundary condition lebih mudah digunakan:
dengan A adalah luas permukaan, adalah perbedaan suhu, q adalah aliran panas per satuan waktu, dan h adalah koefisien perpindahan panas.
Untuk sistem lainnya yang mengandung aliran turbulen, geometri kompleks atau boundary condition maka persamaan lainnya dapat digunakan:
dengan A adalah luas permukaan, } adalah perbedaan termperatur, q adalah aliran panas per satuan waktu dan h adalah koefisien transfer panas.
Ada 2 tipe konveksi yang dapat muncul:
Konveksi tak bebas dapat muncul pada aliran laminer maupun turbulen. Pada kondisi laminer pada tabung berbentuk lingkaran, ada beberapa besaran tak berdimensi seperti bilangan Nusselt, bilangan Reynolds, dan Prandtl. Persamaan yang umum adalah:
Perpindahan panas dianalisis pada packed bed, reaktor, dan alat penukar panas (heat exchanger).
Baca juga ? Konduksi Panas dan Hukum Fourier – Rumus, Contoh Soal dan Jawaban
Konduksi
Pada skala mikroskopik, konduksi panas muncul sebagai “rasa panas”, atom yang bergetar atau berpindah sedemikian cepat berinteraksi dengan atom dan molekul sekelilingnya sehingga memindahkan sejumlah energi mereka ke partikel di sekelilingnya.
Dengan kata lain, panas dipindahkan dengan konduksi ketika atom yang saling berdampingan menggetarkan satu sama lain, atau ketika elektron berpindah dari satu atom ke atom lain. Konduksi adalah bentuk perpindahan panas paling umum pada benda padat pada kontak termal.
Fluida-terutama gas-kurang konduktif. Konduktansi kontak termal adalah studi konduksi panas antara benda padat yang saling bersentuhan.
Konduksi steady state (lihat Hukum Fourier) adalah bentuk konduksi yang terjadi ketika perbedaan temperatur yang terjadi pada konduksi berlangsung spontan, maka setelah waktu kesetimbangan, distribusi spasial temperatur pada benda terkonduksi tidak berubah-ubah lagi. Pada konduksi steady state, jumlah panas yang memasuki suatu bagian sama dengan jumlah panas yang keluar.
Konduksi transient (lihat persamaan panas) muncul ketika temperatur objek berubah sebagai fungsi waktu. Analisis pada sistem transient lebih kompeks dan sering dipakai untuk aplikasi dari analisis numerik oleh komputer.
Rumus perpindahan kalor secara konduksi
Q/t = kA [ (T1-T2) / 1 ]
Keterangan : Q/t = laju perpindahan kalor, k = konduktivitas termal, A = luas penampang, T1 = suhu tinggi, T2 = suhu rendah, l = panjang benda.
Contoh perpindahan kalor secara konduksi
Benda yang terbuat dari logam akan terasa panas, hangat jika benda tersebut dipanaskan, contohnya
- Knalpot motor yang menjadi panas pada saat mesin motor dihidupkan.
- Mentega yang dipanaskan pada wajan yang menjadi meleleh disebabkan karena panas.
- Tutup panci terasa panas saat panci digunakan untuk memasak
- Air akan mendidih pada saat dipanaskan dengan menggunakan panci logam dan sejenisnya.
- Memasak air dengan menggunakan panci logam. Panas panci yang berasal dari kompor yang digunakan saat memasak.
- Membuat kopi atau lain sebagainya minuman panas.
- Membakar besi, logam, dan juga sejenisnya.
- Pada saat memegang gelas yang panas, maka telapak tangan kita juga akan menerima panas dari gelas tersebut.
- Saat menyetrika baju, panas yang berasal dari setrika berpindah ke baju karena digosokkan dengan secara langsung sehingga baju tersebut menjadi hangat.
Pengertian Konduktivitas Termal (keterhantaran termal)
Konduktivitas termal suatu benda merupakan kemampuan yang dimiliki suatu benda dalam memindahkan kalor melalui benda tersebut. Benda yang mempunyai konduktivitas termal (k) yang tinggi maka merupakan penghantar kalor yang baik, begitu sebaliknya. Benda yang mempunyai konduktivitas termal (k) yang renda maka merupakan penghantar kalor yang buruk. Berikut ini merupakan tabel konduktivitas dariberbagai macam benda.
Konduktivitas atau keterhantaran termal adalah suatu besaran intensif bahan yang menunjukkan kemampuannya untuk menghantarkan panas. Konduksi termal adalah suatu fenomena transport di mana perbedaan temperatur menyebabkan transfer energi termal dari satu daerah benda panas ke daerah yang sama pada temperatur yang lebih rendah. Panas yang di transfer dari satu titik ke titik lain melalui salah satu dari tiga metode yaitu konduksi, konveksi, dan radiasi.
- konduktivitas termal = laju aliran panas × jarak / ( luas × perbedaan suhu )
Besaran ini didefinisikan sebagai panas, Q, yang dihantarkan selama waktu t melalui ketebalan L, dengan arah normal ke permukaan dengan luas A yang disebabkan oleh perbedaan suhu ΔT dalam kondisi tunak (adalah kondisi sewaktu sifat-sifat suatu sistem tak berubah dengan berjalannya waktu atau dengan kata lain, konstan) dan jika perpindahan panas hanya tergantung dengan perbedaan suhu tersebut.
Rumus Tahanan Termal (R)
R = T/Q
Keterangan :
R = tahanan alias hambatan termal
Q = konduktivitas termal
T = temperatur
Baca juga ? Rumus Termodinamika Entropi – Contoh Soal dan Jawaban Termodinamika Entropi
Nilai konduktivitas termal berbagai bahan pada 0℃
1. Bahan Logam Konduktivitas termal(k) W/M ℃
Perak(murni) 410
Tembaga(murni) 385
Alumunium (murni) 202
Nikel(murni) 93
Besi(murni) 73
Baja karbon,1% 43
Timbal (murni) 35
Baja krom – nikel (18%Cr,8%Ni) 16.
2. Bahan Logam Konduktivitas Bukan Logam (k) W/M ℃
Kuarsa(sejajar sumbu) 41.6
Magnesit 4.15
Marmer 2.08-2.94
Batu pasir 1.83
Kaca, jendela 0.78
Kayu, maple atau ek 0.17
Serbuk gergaji 0.059
Wol kaca 0.038
3. Berikut ini nilai konduktivitas termal beberapa benda
| Jenis benda | Konduktivitas Termal (k) | |
| J/m.s.Co | Kkal/m.s.Co | |
| Perak | 420 | 1000 x 10-4 |
| Tembaga | 380 | 920 x 10-4 |
| Aluminium | 200 | 500 x 10-4 |
| Baja | 40 | 110 x 10-4 |
| Es | 2 | 5 x 10-4 |
| Kaca (biasa) | 0,84 | 2 x 10-4 |
| Bata | 0,84 | 2 x 10-4 |
| Air | 0,56 | 1,4 x 10-4 |
| Tubuh manusia | 0,2 | 0,5 x 10-4 |
| Kayu | 0,08 – 0,16 | 0,2 x 10-4 – 0,4 x 10-4 |
| Gabus | 0,042 | 0,1 x 10-4 |
| Wol | 0,040 | 0,1 x 10-4 |
| Busa | 0,024 | 0,06 x 10-4 |
| Udara | 0,023 | 0,055 x 10-4 |
2. Adveksi
Perpindahan energi dari satu lokasi ke lokasi lain sebagai efek samping dari objek berenergi yang bergerak.
3. Radiasi
Perpindahan energi dari atau ke objek akibat pelepasan atau penyerapan radiasi elektromagnetik serta tidak harus melakukan kontak fisik dengan sumber panas.
Rumus Perpindahan Kalor Radiasi
Laju perpindahan kalor termal yang dipancarkan dengan cara radiasi oleh suatu benda secara empiris ditemukan oleh Josef Stefan di tahun 1879. Stefan mengemukakan bahwa laju perpindahan kalor termal yang dipancarkan secara radiasi oleh suatu benda sebanding dengan luas permukaan pada benda dan pangkat empat suhu absolutnya. Hasil empiris diturunkan dengan teoritis oleh Ludwig Boltzmann di tahun 1884 yang dikenal dengan hukum Stefan-Boltzmann yang bisa dinyatakan dengan persamaan sebagai berikut:
P = eσAT44
Dengan keterangan:
P = Daya yang diradiasikan (watt)
e = Emisivitas suatu benda
σ = Konstanta Stefan (5,6703 x 10-8 W/m2K4).
A =Luas suatu benda yang memancarkan radiasi (m2)
T = Suhu mutlak (K)
Nilai emisivitas e sebuah benda bergantung dengan warna permukaan suatu benda tersebut. Permukaan sebuah benda yang berwarna hitam sempurna nilai e = 1, sedang untuk suatu benda yang warnanya putih sempurna nilai e = 0. Jadi nilai emisivitas e secara umum adalah 0 < e < 1.
Contoh Soal Perpindahan Kalor Radiasi
1. Sebuah bola tembaga memiliki luas 20 cm2 selanjutnya dipanaskan sampai berpijar pada suhu 127o Apabila emisivitas bahan adalah 0,4 dan tetapan Stefan adalah 5,67 x 10-8 W/m2K4, maka hitunglah energi radiasi yang dipancarkan oleh bola tersebut setiap sekonnya.
Penyelesaian:
Diketahui:
A = 20 cm2 = 2 x 10-3 m2
T = (127 + 273) = 400 K
e = 0,4
σ = 5,67 x 10-8 W/m2K4
Ditanya: P:…?
Jawab:
P = eσAT4
P = (0,4).(5,67 x 10-8).(2 x 10-3).(400)4
P = (0,4).(5,67 x 10-8).(2 x 10-3).(256 x 108)
P = 1161,23 x 10-3 W
P = 1,61123 W ≈ 1,2 W
Jadi, energi radiasi yang dipancarkan oleh suatu bola tersebut pada setiap sekon adalah 1,2 watt.
Contoh radiasi:
- Panas matahari yang sampai ke bumi walau dengan melalui ruang hampa.
- Tubuh terasa hangat pada saat berada di dekat sumber api.
- Menetaskan telur unggas dengan menggunakan lampu.
- Pakaian menjadi kering pada saat dijemur di bawah terik matahari.
- warna hitam kusam merupakan penyerap atau pemancar kalor yang baik
- radiasi neutron cepat atau lambat.
Radiasi termal
Radiasi termal adalah energi yang dilepaskan oleh benda sebagai gelombang elektromagnetik, karena adanya tumpukan energi termal pada semua benda dengan suhu di atas nol mutlak.
Radiasi termal muncul sebagai akibat perpindahan acak dari atom dan molekul benda. Karena atom dan molekul ini terdiri dari partikel bermuatan (proton dan elektron), pergerakan mereka menghasilkan pelepasan radiasi elektromagnetik yang membawa energi.
Radiasi dari matahari dapat digunakan untuk panas dan tenaga listrik. Tidak seperti konduksi dan konveksi, radiasi termal dapat dikumpulkan di sebuah titik kecil menggunakan kaca pemantul, kemudian dimanfaatkan untuk pembangkit listrik solar.
Rumus Radiasi
∆Q ∆t = e.
Q = Kalor yang dipancarkan benda (J)
T = suhu mutlak (K)
e = emisitas bahan
σ = Tetapan Stefan Boltzman (5,672 x 10-8 W/m2K4 )
A = Luas Penampang benda (m2)
Contoh Soal Radiasi:
Sebuah lampu pijar memakai kawat wolfram dengan luas (A) 10-6 m2 dan emisivitasnya (e) 0,5. Jika bola lampu berpijar dengan suhu 1.000 K selama 5 second (σ = 5,67 x 10-8 W/m2K4 ), maka hitunglah jumlah energi radiasi yang dipancarkan oleh lampu pijar tersebut!
Diketahui:
T = 1.000 K
A = 10-6 m2
t = 5 s
e = 0,5
σ = 5,67 x 10-8 W/m2K4
Pertanyaan: Q
Jawaban:
∆Q/∆t = e σ A T4
∆Q = e σ A T4 ∆t
= (0,5) (5,67 x 10-8 W/m2K4 ) (10-6 m2) (1.000 K)4(5s)
= 14,175 x 10-2 J
4. Konveksi
Perpindahan panas konveksi atau konveksi adalah perpindahan panas dari satu tempat ke tempat lain karena adanya perpindahan fluida, proses perpindahan panas melalui perpindahan massa. Gerak serempak fluida menambah perpindahan panas pada banyak kondisi, seperti misalnya antara permukaan solid dan permukaan fluida. Konveksi adalah perpindahan panas yang umum pada cairan dan gas.
Konveksi bebas muncul ketika gerak fluida disebabkan oleh gaya apung yang berasal dari perbedaan massa jenis akibat perbedaan temperatur di dalam fluida. Konveksi tak bebas adalah istilah yang digunakan ketika aliran di dalam fluida diinduksi oleh benda eksternal, seperti kipas, pengaduk, dan pompa, sehingga menyebabkan konveksi induksi buatan.
Pendinginan atau pemanasan konveksi di banyak kasus dapat dijelaskan oleh Hukum Newton tentang pendinginan: “Kecepatan hilangnya panas pada benda sebanding dengan perbedaan temperatur antara benda tersebut dengan lingkungannya.” Meskipun begitu, dari definisinya, hukum Newton tentang pendinginan ini membutuhkan kecepatan panas hilang yang membentuk garis linear pada grafik fungsi (“sebanding dengan”). Padahal, secara umum, konveksi tidak pernah membentuk gradien garis lurus. Maka, hukum Newton tidak berlaku.
Rumus Konveksi
H = h. A. ∆T
Keterangan:
h = Koefisien konveksi termal (j/sm2K)
A = Luas permukaan (m2)
∆ T = Perbedaan suhu (K)
Contoh Soal Konveksi:
Suatu Fluida memiliki koefisien konveksi termal 0,01 kal/ms0C dan memiliki luas penampang aliran 20 cm2.
Bila fluida tersebut mengalir di sebuah dinding dengan suhu 1000C menuju dinding lainya dengan suhu 200C dan kedua dinding dalam keadaan yang sejajar, maka berapa besarnya kalor yang dirambatkan?
Diketahui:
h = 0,01 kal/ms0C
A = 20 cm2 = 2 x 10-3 m2
∆ T = (1000C-200C) = 800C
Jawaban:
H = h A ∆ T
= (0,01 kal/ms0C) (2 x 10-3 m2) (800C)
= 16 x 10-4 kal/s
Persamaan perpindahan panas konveksi dikenal sebagai hukum Newton untuk pendinginan (Newton’s Law of Cooling) yang dipersamaankan sebagai berikut:
JikaTs>T∞ maka:
Dengan,
| qKonv | : | Laju perpindahan panas konveksi (Watt) |
| h | : | Koefisien perpindahan panas konveksi (W/m2 .K) |
| A | : | Luas permukaan perpindahan panas (m2) |
| T∞ | : | Temperatur permukaan (K) |
| Ts | Temperatur fluida (K) |
Besarnya perpindahan panas konveksi juga ditentukan oleh besarnya koefisien perpindahan panas konveksi (h) yang tergantung dari dimensi dan kondisi aliran. Kondisi aliran untuk konveksi alami ditentukan dari Rayleigh Number (RaL) yaitu perkalian antara Grashof Number (GrL) dengan Prandtl Number (Pr), sehingga secara matematis dapat ditulis sebagai berikut :
Dengan,
| g | : | Percepatan gravitasi (m/s2) |
| β | : | Koefisien ekspansi volume (1/K) |
| Ts | : | Temperatur permukaan (K) |
| T∞ | : | Temperatur dari fluida (K) |
| Lc | : | Panjang karakteristik (m) |
| v | : | Viskositas kinematik fluida (m2/s) |
Apabila : RaL > 109 aliran adalah turbulen ; RaL ≈ 109 kondisi kritis ; RaL < 109 aliran adalah laminar.
Untuk perpindahan panas konveksi alami pada plat datar vertikal Nusselt Number ditentukan dengan persamaan :
Sedangkan untuk perpindahan panas konveksi alami pada plat datar horizontal penentuan harga Nusselt Number dibagi menjadi dua :
- Untuk plat horizontal dengan arah perpindahan panas ke atas,
Nu = 0,54 RaL1/4 untuk 10=<RaL<107
Nu = 0,15,RaL1/3 untuk 107<RaL<1011
- Untuk plat horizontal dengan arah perpindahan panas ke bawah,
Nu = 0,27 RaL ¼ dengan : 105<RaL<1011
Koefisien perpindahan panas konveksi (h) ditentukan dengan Nusselt Number (Nu).
Nu =HLc/K sehingga Nu =Nuk/Lc
Dengan,
| Nu | : | Nusselt Number |
| H | : | Koefisien perpindahan panas konveksi (W/m2 .K) |
| K | : | Konduktivitas temal fluida (W/m .K) |
| Lc | : | Panjang karakteristik (m) |
Contoh Konveksi:
- Gerakan naik dan turun air ketika dipanaskan.
- Gerakan naik dan turun kacang hijau, kedelai dan lainnya ketika dipanaskan.
- Terjadinya angin darat dan angin laut.
- Gerakan balon udara.
- Asap cerobong pabrik yang membumbung tinggi.
- Ketika kita merebus kacang hijau pada saat airnya sudah memdidih maka ada pergerakan naik turun dari kacang hijau.
- Pada saat kita merebus air maka akan ada pergerakan air yang panas naik dan juga yang dingin turun.
- Terjadinya angin darat serta jugaangin laut, karena adanya suatu perbedaan pada suhu di daratan danjuga tentu di lautan.
- Saat memanaskan air, air akan terlihat seperti diaduk. Itu disebabkan karena, air yang paling bawah akan pertama kalilebih dulu panas dan juga menjadi akan menjadi lebih ringan sehingga saat berpindah ke atas.
- Proses mencairnya es batu yang dimasukkan ke dalam air panas. Panas pada air tersebut berpindah secara bersamaan dengan mengalirnya air panas itu ke es batu.
Baca juga ? Entalpi Termokimia – Pemanasan / Kalor Fisika – Soal dan Jawaban
Koefisien perpindahan panas
di mana
- ΔQ = panas yang masuk atau panas yang keluar, W
- h = koefisien perpindahan panas, W/(m2K)
- A = luas permukaan perpindahan panas, m2
- = perbedaan temperatur antara permukaan padat dengan luas permukaan kontak dengan fluida, K
Dari persamaan di atas, koefisien perpindahan panas adalah koefisien proporsionalitas antara fluks panas, Q/(A delta t), dan perbedaan temperatur, , yang menjadi penggerak utama perpindahan panas.
Satuan SI dari koefisien perpindahan panas adalah watt per meter persegi-kelvin, W/(m2K). Koefisien perpindahan panas berkebalikan dengan insulasi termal.
Terdapat beberapa metode untuk mengkalkulasi koefisien perpindahan panas dalam berbagai jenis kondisi perpindahan panas yang berbeda, fluida yang berlainan, jenis aliran, dan dalam kondisi termohidraulik.
Perhitungan koefisien perpindahan panas dapat diperkirakan dengan hanya membagi konduktivitas termal dari fluida dengan satuan panjang, namun untuk perhitungan yang lebih akurat sering kali digunakan bilangan Nusselt, yaitu satuan tak berdimensi yang menunjukkan rasio perpindahan panas konvektif (pergerakan molekul-molekul pada fluida yaitu cairan atau gas dan rheid) dan konduktif normal terhadap bidang batas.
Korelasi Dittus-Boelter (konveksi paksa, forced convection)
Korelasi yang khusus namun sederhana dan biasa digunakan pada berbagai aplikasi adalah korelasi perpindahan panas Dittus-Boelter untuk fluida dalam aliran turbulen. Korelasi ini dapat digunakan ketika konveksi adalah satu-satunya cara dalam memindahkan panas, tidak ada perubahan fase, dan tidak ada radiasi yang signifikan. Koreksi dari perhitungan ini ±15%.
Untuk aliran fluida pada pipa melingkar yang lurus dengan bilangan Reynolds antara 10000 dan 120000, ketika bilangan Prandtl di anara 0.7 dan 120, untuk titik yang jaraknya lebih dari sepuluh kali diameter pipa dan ketika permukaan pipa halus secara hidraulis, koefisien perpindahan panas antara fluida dan permukaan pipa dapat diekspresikan sebagai:
di mana
- = konduktivitas termal fluida
- = = diameter hidraulik
- Nu = bilangan Nusselt
bilangan Nusselt dapat dicari dengan:
- (korelasi Dittus-Boelter)
di mana:
- Pr = bilangan Prandtl
- Re = bilangan Reynolds
- n = 0.4 untuk pemanasan (dinding lebih panas dari fluida yang mengalir) dan 0.33 untuk pendinginan (dinding lebih dingin dari fluida yang mengalir).
Korelasi Thom
Terdapat korelasi yang sederhana antara koefisien perpindahan panas dalam proses pemanasan fluida hingga mendidih (boiling process). Korelasi Thom adalah untuk aliran air yang mendidih dan jenuh pada tekanan di atas 20 MPa, dalam kondisi di mana molekul-molekul air yang mendidih lebih banyak mendominasi sepanjang konveksi paksa sedang terjadi. Konsep ini berguna untuk perkiraan kasar dari perbedaan temperatur yang mungkin terjadi pada fluks panas yang ditentukan.
di mana:
- = kenaikan temperatur pada dinding di atas titik jenuh, K
- q = fluks panas, MW/m2
- P = tekanan air, MPa
perhatikan bahwa ini adalah rumus empiris yang khusus pada satuan tertentu yang diberikan pada rumus.
Koefisien perpindahan panas pada dinding pipa
Pada kasus perpindahan panas pada pipa yang melingkar, fluks panas bergantung pada diameter dalam dan diameter luar dari pipa, atau tebalnya. Namun jika tebal pipa sangat tipis jika dibandingkan dengan diameter dalamnya, maka perhitungannya:
di maka k adalah konduktivitas termal dari material dinding dan x adalah ketebalan dinding. Penggunaan asumsi ini bukan berarti mengasumsikan bahwa ketebalan dinding diabaikan, namun diasumsikan bahwa perpindahan panas adalah linier pada satu garis, tidak tersebar dari satu titik di pusat pipa ke segala arah penampang melintang pipa.
Jika asumsi di atas tidak berlaku, maka koefisien perpindahan panas dapat dihitung dengan menggunakan:
di mana di adalah diameter dalam dan do adalah diameter luar.
Koefisien perpindahan panas gabungan
Untuk dua atau lebih proses perpindahan panas yang bekerja secara paralel, koefisien perpindahan panas ditambahkan:
Untuk dua atau lebih proses perpindahan panas yang bekerja secara berantai pada garis lurus, koefisien perpindahan panas ditambahkan secara invers:
Misalnya, katakan ada sebuah pipa dengan fluida yang mengalir di dalamnya. Laju perpindahan panas antara fluida di bagian dalam pipa dengan permukaan luar pia adalah
di mana
- Q = laju perpindahan panas (W)
- h = koefisien perpindahan panas (W/(m2·K))
- t = ketebalan dinding (m)
- k = konduktivitas termal dinding (W/m·K)
- A = luas permukaan dinding (m2)
- = perbedaan temperatur.
Aplikasi koefisien perpindahan panas
Koefisien perpindahan panas banyak digunakan dalam perhitungan dan permodelan proses pengeringan, pengolahan makanan (misalnya penggorengan, pemasakan dengan manipulasi tekanan (puffing), dsb), hingga permodelan suhu udara di dalam bangunan (misalnya rumah tanaman atau greenhouse).
Rumus Fisika Lainnya
Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).
Contoh Soal dan Jawaban Perpindahan Panas (Kalor)
1. Sebuah sistem termal silinder memiliki diameter luar 50 mm, tinggi 15 cm, dan temperatur permukaan luarnya 227 °C. Silinder tersebut berada di dalam lingkungan udara atmosfer yang bertemperatur rata-rata 27 °C dengan koefisien perpindahan panas konveksi 50 W/m²K. Pada kasus ini kita ingin memperoleh gambaran seberapa besar laju transmisi energi panas dari permukaan silinder bagian luar ke sirkulasi udara di sekitarnya, dan besarnya tahanan termal konveksinya.
Pembahasan:
Prinsip-prinsip perhitungannya adalah sebagai berikut:
Dalam persoalan ini, kita anggap bahwa perpindahan panas radiasi dianggap kecil sehingga diabaikan. Besarnya laju perpindahan panas konveksi dari permukaan silinder ke udara di sekitarnya dihitung dengan menggunakan persamaan:
Q34 = hoAo (T3 – T4)
Disini:
T3 = temperatur permukaan luar silinder 227 °C
T4 = temperatur udara luar 27 °C
ho = koefisien perpindahan panas konveksi aliran udara 50 W/m²K
Gunakan rumus: Ao = π do L
Dengan menggunakan data:
do adalah diameter luar silinder, diketahui = 50 mm = 0,05
L tinggi silinder, diketahui = 15 cm = 0,15 m
Maka diperoleh Ao = 0,0236 m²
Selanjutnya dengan menggunakan data-data tersebut, sekarang kita dapat menghitung besarnya laju perpindahan panas konveksi menggunakan persamaan:’
Q34 = ho Ao (T3 – T4)
Maka diperoleh Q34 = 234,5 W.
2. Soal perhitungan konveksi.Udara pada suhu 23°C bertiup diatas plat panas berukuran (60×80) cm. Suhu plat dijaga tetap 300°C. Koefisien perpindahan kalor konveksi adalah 20 W/m² °C. Hitung berapa nilai perpindahan kalornya!
Jawaban:
Hukum newton tentang pendinginan:
q = h.A.(Tw-T∞)
q = 20 W/m². 0°C . (0,6×0,8)m² . (300-23)°C
q = 2659,2W
q = 2,659KW
3. Soal perpindahan kalor radiasi. Plat A dan plat B merupakan dua plat
tak berhingga (blackbody). Suhu plat A adalah 700 °C dan suhu plat B adalah 450 °C. Pada kedua plat tersebut saling terjadi perpindahan kalor secara radiasi. Hitung perpindahan kalor netto per satuan luas!
Jawaban:
Suhu mutlak plat A = (700+273)°K = 973°K
Suhu mutlak plat B = (450+273)°K = 723°K
Dengan menggunakan persamaan:
q pancaran netto / A = σ . (T14 – T24)
q pancaran netto / A = 5,699 x 10-8 W/m² . K4 . (973³4 – 723^4)K^4
q pancaran netto / A = 3,53207 x 104 W/m²
q pancaran netto / A = 35,2 KW/m²
Rumus Fisika Lainnya
Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).
Bacaan Lainnya
- Sifat Atom – 10 Sifat Dasar Atom (Nuklir, Massa, Ukuran, Momen magnetik, Aras energi)
- Jari-Jari Atom – Jenis dan Nilai jari-jari atom
- Atom – Pengertian, Teori, Sifat, Struktur, Susunan
- Konfigurasi Elektron – Penjelasan Tabel konfigurasi elektron
- Reduktor dan Oksidator – Penjelasan, Contoh Soal dan Jawaban
- Bilangan Oksidasi Kimia (Biloks) – Aturan Penentuan Biloks, Tabel, Contoh Soal dan Jawaban
- Pembakaran Kimia – Persamaan Kimia – Sempurna & Tak Sempurna dan Contoh Soal beserta Jawabannya
- Tabel Periodik Lengkap Dengan Daftar Unsur Kimia Berdasarkan Nama, Warna dan Jenis
- Rumus Kimia Konsep Mol dan Empiris Beserta Contoh Soal & Jawaban
- Unsur, Senyawa dan Campuran Kimia – Beserta Penjelasan & Rumus
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
- Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
- Cara Menghentikan Penindasan Bullying
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- 10 Cara Memotivasi Anak Untuk Belajar Agar Menjadi Pintar
- Di Indonesia, (HAN) Hari Anak Nasional tanggal 23 Juli
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Colorado State University, Science Direct, Machine Design
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing
























Wah keren artikelnya. Terima kasih yah. Jadi teringat masa sekolah dulu 🙂
Sama-sama 🙂