Perkalian Vektor

Perkalian Vektor adalah operasi perkalian dengan dua operand (objek yang dikalikan) berupa vektor. Tetapi hasil operasi ini tidak selalu adalah vektor. Terdapat 3 macam perkalian vektor, yaitu: produk skalar atau perkalian titik (bahasa Inggris: dot product atau scalar product, perkalian silang (bahasa Inggris: cross product atau vector product atau directed area product) dan perkalian langsung (bahasa Inggris: direct product).

Produk Skalar Vektor atau Perkalian Titik

Produk skalar (atau “perkalian titik”) dua buah vektor akan menghasilkan sebuah skalar. Jenis perkalian ini bersifat komutatif.

\!{\vec {A}}\cdot {\vec {B}}=(a_{x}{\hat {i}}+a_{y}{\hat {j}}+a_{z}{\hat {k}})\cdot (b_{x}{\hat {i}}+b_{y}{\hat {j}}+b_{z}{\hat {k}})

=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}\!

Untuk vektor satuan terdapat hubungan-hubungan yang khusus dalam operasi perkalian titik, yang merupakan sifat-sifat yang digunakan dalam perkalian titik, yaitu

{\hat {i}}\cdot {\hat {i}}=1

{\hat {j}}\cdot {\hat {j}}=1

{\hat {k}}\cdot {\hat {k}}=1

dan

{\hat {i}}\cdot {\hat {j}}={\hat {j}}\cdot {\hat {i}}=0

{\hat {j}}\cdot {\hat {k}}={\hat {k}}\cdot {\hat {j}}=0

{\hat {k}}\cdot {\hat {i}}={\hat {i}}\cdot {\hat {k}}=0

Atau dapat pula dituliskan dengan menggunakan notasi delta Kronecker $\!\delta _{mn}$ , yaitu

{\hat {m}}\cdot {\hat {n}}=\delta _{mn}

Perkalian Silang Vektor

Hasil suatu perkalian silang dua buah vektor adalah juga sebuah vektor. Perkalian silang bersifat tidak komutatif.

{\vec {A}}\times {\vec {B}}=(a_{x}{\hat {i}}+a_{y}{\hat {j}}+a_{z}{\hat {k}})\times (b_{x}{\hat {i}}+b_{y}{\hat {j}}+b_{z}{\hat {k}})

=(a_{y}b_{z}-a_{z}b_{y}){\hat {i}}+(a_{z}b_{x}-a_{x}b_{z}){\hat {j}}+(a_{x}b_{y}-a_{y}b_{x}){\hat {k}}

Untuk vektor-vektor satuan terdapat pula hubungan yang mendasari operasi perkalian silang, yaitu

{\hat {i}}\times {\hat {j}}={\hat {k}}

{\hat {j}}\times {\hat {k}}={\hat {i}}

{\hat {k}}\times {\hat {i}}={\hat {j}}

dan

{\hat {j}}\times {\hat {i}}=-{\hat {k}}

{\hat {k}}\times {\hat {j}}=-{\hat {i}}

{\hat {i}}\times {\hat {k}}=-{\hat {j}}.

Perkalian langsung Vektor

Hasil perkalian langsung dua buah vektor adalah sebuah tensor atau matriks. Perkalian ini tidak bersifat komutatif.

{\vec {A}}{\vec {B}}=(a_{x}{\hat {i}}+a_{y}{\hat {j}}+a_{z}{\hat {k}})(b_{x}{\hat {i}}+b_{y}{\hat {j}}+b_{z}{\hat {k}})

={\hat {i}}(a_{x}b_{x}){\hat {i}}+{\hat {i}}(a_{x}b_{y}){\hat {j}}+{\hat {i}}(a_{x}b_{z}){\hat {k}}

+{\hat {j}}(a_{y}b_{x}){\hat {i}}+{\hat {j}}(a_{y}b_{y}){\hat {j}}+{\hat {j}}(a_{y}b_{z}){\hat {k}}

+{\hat {k}}(a_{z}b_{x}){\hat {i}}+{\hat {k}}(a_{z}b_{y}){\hat {j}}+{\hat {k}}(a_{z}b_{z}){\hat {k}}

Perkalian langsung dua buah vektor satuan tidak memiliki hubungan yang khusus.

({\hat {a}})({\hat {b}})={\hat {a}}{\hat {b}}

{\hat {a}}{\hat {b}}\neq {\hat {b}}{\hat {a}}

Produk Skalar / Perkalian Titik

Definisi menurut aljabar

Produk skalar dua vektor A = [A₁, A₂, …, A_n] dan B = [B₁, B₂, …, B_n] didefinisikan sebagai:

\mathbf {A} \cdot \mathbf {B} =\sum _{i=1}^{n}A_{i}B_{i}=A_{1}B_{1}+A_{2}B_{2}+\cdots +A_{n}B_{n}

di mana Σ melambangkan summation notation dan n adalah dimensi ruang vektor. Misalnya, dalam ruang tiga dimensi, produk skalar vektor-vektor [1, 3, −5] dan [4, −2, −1] adalah:

{\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=(1)(4)+(3)(-2)+(-5)(-1)\\&=4-6+5\\&=3.\end{aligned}}

Definisi menurut geometri

Dalam ruang Euclidean, suatu vektor Euclidean adalah sebuah objek geometri yang memiliki baik besaran (magnitude) dan arah (direction). Sebuah vektor dapat digambarkan seperti sebuah anak panah. Besarannya adalah panjangnya, sedangkan arahnya adalah yang ditunjuk oleh ujung panah. Besaran vektor A dilambangkan dengan $\|\mathbf {A} \|$ . Produk skalar dua vektor Euclidean A dan B didefinisikan sebagai:

\mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,

di mana θ adalah sudut di antara A dan B.

Secara khusus, jika A dan B adalah ortogonal, maka sudut di antara keduanya adalah 90° dan

\mathbf {A} \cdot \mathbf {B} =0.

Pada keadaan ekstrem lain, jika kedua vektor itu mempunyai arah yang sama (codirectional), maka sudut di antara keduanya adalah 0° dan

\mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|

Ini menyiratkan bahwa produk skalar suatu vektor A dengan dirinya sendiri adalah

\mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2},

yang menghasilkan

\|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }},

rumus untuk panjang Euclidean vektor itu.

Sifat Produk Skalar / Perkalian Titik

Produk skalar memenuhi sifat-sifat berikut jika a, b, dan c adalah vektor real dan r adalah suatu bilangan skalar.

Komutatif:
$\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$
which follows from the definition (θ is the angle between a and b):
$\mathbf {a} \cdot \mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\cos \theta =\|\mathbf {b} \|\|\mathbf {a} \|\cos \theta =\mathbf {b} \cdot \mathbf {a}$
Distributif over vector addition:
$\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$
Bilinear:
$\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$
Perkalian skalar:
$(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=c_{1}c_{2}(\mathbf {a} \cdot \mathbf {b} )$
Ortogonal:
Dua vektor bukan-nol a dan b adalah ortogonal jika dan hanya jika a ⋅ b = 0.
Tidak ada cancellation:
Berbeda dengan perkalian angka biasa, di mana jika ab = ac, maka b selalu sama dengan c kecuali a sama dengan nol, produk skalar tidak menuruti cancellation law:
Jika a ⋅ b = a ⋅ c dan a ≠ 0, maka dapat ditulis: a ⋅ (b − c) = 0 dengan hukum distributif; hasil di atas mengatakan bahwa ini hanya berarti a tegak lurus dengan (b − c), di mana masih mengizinkan (b − c) ≠ 0, sehingga b ≠ c.
Product Rule: Jika a dan b adalah suatu fungsi, maka turunan (dilambangkan oleh tanda prime ′) dari a ⋅ b adalah a′ ⋅ b + a ⋅ b′.

Posisi vektor

${\vec {a}}=(a_{1},a_{2})={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}=a_{1}{\hat {i}}+a_{2}{\hat {j}}$

{\vec {a}}=(a_{1},a_{2},a_{3})={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}=a_{1}{\hat {i}}+a_{2}{\hat {j}}+a_{3}{\hat {k}}

Panjang vektor

Berada di $R^{2}$

Panjang vektor a dalam posisi

(a_{1},a_{2})

adalah

\left|{\vec {a}}\right|={\sqrt {a_{1}^{2}+a_{2}^{2}}}

Panjang vektor b dalam posisi

(b_{1},b_{2})

adalah

\left|{\vec {b}}\right|={\sqrt {b_{1}^{2}+b_{2}^{2}}}

Panjang vektor c dalam posisi

(a_{1},a_{2})

dan

(b_{1},b_{2})

adalah

\left|{\vec {c}}\right|={\sqrt {(b_{1}-a_{1})^{2}+(b_{2}-a_{2})^{2}}}

Berada di $R^{3}$

Panjang vektor a dalam posisi

(a_{1},a_{2},a_{3})

adalah

\left|{\vec {a}}\right|={\sqrt {a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}

Panjang vektor b dalam posisi

(b_{1},b_{2},b_{3})

adalah

\left|{\vec {b}}\right|={\sqrt {b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}

Panjang vektor c dalam posisi

(a_{1},a_{2},a_{3})

dan

(b_{1},b_{2},b_{3})

adalah

\left|{\vec {c}}\right|={\sqrt {(b_{1}-a_{1})^{2}+(b_{2}-a_{2})^{2}+(b_{3}-a_{3})^{2}}}

Vektor satuan

{\hat {a}}={\frac {\vec {a}}{\left|{\vec {a}}\right|}}

Operasi aljabar pada vektor

Penjumlahan dan pengurangan

terdiri dari 2 aturan jenis yaitu aturan segitiga dan jajar genjang

{\vec {c}}={\vec {a}}+{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}+{\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}={\begin{pmatrix}{a_{1}+b_{1}}\\{a_{2}+b_{2}}\end{pmatrix}}

{\vec {c}}={\vec {a}}-{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}-{\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}={\begin{pmatrix}{a_{1}-b_{1}}\\{a_{2}-b_{2}}\end{pmatrix}}

Perkalian

skalar dengan vektor

Jika k skalar tak nol dan vektor ${\vec {a}}=a_{1}{\hat {i}}+a_{2}{\hat {j}}+a_{3}{\hat {k}}$ maka vektor $k{\vec {a}}=(ka_{1},ka_{2},ka_{3})$

titik dua vektor

Jika vektor ${\vec {a}}=a_{1}{\hat {i}}+a_{2}{\hat {j}}+a_{3}{\hat {k}}$ dan vektor ${\vec {b}}=b_{1}{\hat {i}}+b_{2}{\hat {j}}+b_{3}{\hat {k}}$ maka ${\vec {a}}\cdot {\vec {b}}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$

titik dua vektor dengan membentuk sudut

Jika ${\vec {a}}$ dan ${\vec {b}}$ vektor tak nol dan sudut $\alpha$ diantara vektor ${\vec {a}}$ dan ${\vec {b}}$ maka perkalian skalar vektor ${\vec {a}}$ dan ${\vec {b}}$ adalah ${\vec {a}}\cdot {\vec {b}}$ = $\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|cos\alpha$

silang dua vektor

Jika vektor ${\vec {a}}=a_{1}{\hat {i}}+a_{2}{\hat {j}}+a_{3}{\hat {k}}$ dan vektor ${\vec {b}}=b_{1}{\hat {i}}+b_{2}{\hat {j}}+b_{3}{\hat {k}}$ maka ${\vec {a}}\times {\vec {b}}=(a_{2}b_{3}{\hat {i}}+a_{3}b_{1}{\hat {j}}+a_{1}b_{2}{\hat {k}})-(a_{2}b_{1}{\hat {k}}+a_{3}b_{2}{\hat {i}}+a_{1}b_{3}{\hat {j}})$

\left[{\begin{array}{rrr|rr}{\hat {i}}&{\hat {j}}&{\hat {k}}&{\hat {i}}&{\hat {j}}\\a_{1}&a_{2}&a_{3}&a_{1}&a_{2}\\b_{1}&b_{2}&b_{3}&b_{1}&b_{2}\\\end{array}}\right]

Sifat operasi aljabar pada vektor

${\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}$
$({\vec {a}}+{\vec {b}})+{\vec {c}}={\vec {a}}+({\vec {b}}+{\vec {c}})$
${\vec {a}}+0=0+{\vec {a}}$
$k({\vec {a}}+{\vec {b}})=k{\vec {a}}+k{\vec {b}}$
$(k+l){\vec {a}}=k{\vec {a}}+l{\vec {a}}$
${\vec {a}}+(-{\vec {a}})=0$
${\vec {a}}\cdot {\vec {b}}={\vec {b}}\cdot {\vec {a}}$
$({\vec {a}}\cdot {\vec {b}})\cdot {\vec {c}}={\vec {a}}\cdot ({\vec {b}}\cdot {\vec {c}})$
${\vec {a}}\cdot 1=1\cdot {\vec {a}}$
$k({\vec {a}}\cdot {\vec {b}})=k{\vec {a}}\cdot {\vec {b}}={\vec {a}}\cdot k{\vec {b}}$
$(k\cdot l){\vec {a}}=k(l\cdot {\vec {a}})$
${\vec {a}}\cdot {\vec {a}}=\left|{\vec {a}}\right|$
${\vec {a}}\times {\vec {b}}\neq {\vec {b}}\times {\vec {a}}$
${\vec {a}}\times {\vec {b}}=-({\vec {b}}\times {\vec {a}})$
$({\vec {a}}\times {\vec {b}})\times {\vec {c}}\neq {\vec {a}}\times ({\vec {b}}\times {\vec {c}})$
${\vec {a}}\cdot ({\vec {b}}\times {\vec {c}})={\vec {b}}\cdot ({\vec {c}}\times {\vec {a}})={\vec {c}}\cdot ({\vec {a}}\times {\vec {b}})$
${\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}$
$k({\vec {a}}\times {\vec {b}})=k{\vec {a}}\times {\vec {b}}={\vec {a}}\times k{\vec {b}}$

Hubungan vektor dengan vektor lain

Perkalian titik

Saling tegak lurus

Jika tegak lurus antara vektor ${\vec {a}}$ dengan vektor ${\vec {b}}$ maka

{\vec {a}}\cdot {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|cos90

{\vec {a}}\cdot {\vec {b}}=0

Sejajar

Jika vektor ${\vec {a}}$ sejajar dengan vektor ${\vec {b}}$ maka

{\vec {a}}\cdot {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|cos0

{\vec {a}}\cdot {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|

{\vec {a}}\cdot {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|cos180

{\vec {a}}\cdot {\vec {b}}=-\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|

Perkalian silang

Saling tegak lurus

Jika tegak lurus antara vektor ${\vec {a}}$ dengan vektor ${\vec {b}}$ maka

{\vec {a}}\times {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|sin90

{\vec {a}}\times {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|

{\vec {a}}\times {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|sin180

{\vec {a}}\times {\vec {b}}=-\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|

Jika $\beta >90$ maka dua vektor tersebut searah

Jika $\beta <90$ maka vektor saling berlawanan arah

Sejajar

Jika vektor ${\vec {a}}$ sejajar dengan vektor ${\vec {b}}$ maka

{\vec {a}}\times {\vec {b}}=\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|sin0

{\vec {a}}\times {\vec {b}}=0

Sudut dua vektor

Jika vektor ${\vec {a}}$ dan vektor ${\vec {b}}$ sudut yang dapat dibentuk dari kedua vektor tersebut adalah $cos\alpha ={\frac {{\vec {a}}\cdot {\vec {b}}}{\left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|}}$

Panjang proyeksi dan proyeksi vektor

Panjang proyeksi vektor

{\vec {a}}

pada vektor

{\vec {b}}

adalah

\left|{\vec {c}}\right|={\frac {{\vec {a}}\cdot {\vec {b}}}{\left|{\vec {b}}\right|}}

Proyeksi vektor

{\vec {a}}

pada vektor

{\vec {b}}

adalah

{\vec {c}}={\frac {{\vec {a}}\cdot {\vec {b}}}{\left|{\vec {b}}\right|^{2}}}\cdot {\vec {b}}

Perbandingan

Aturan jajar genjang: Posisi vektor; ${\vec {N}}={\frac {ms+nr}{m+n}}$

Berada di

R^{2}

{\vec {N}}=({\frac {mx_{2}+nx_{1}}{m+n}},{\frac {my_{2}+ny_{1}}{m+n}})

Berada di

R^{3}

{\vec {N}}=({\frac {mx_{2}+nx_{1}}{m+n}},{\frac {my_{2}+ny_{1}}{m+n}},{\frac {mz_{2}+nz_{1}}{m+n}})

Satu garis: Perbandingan posisi dalam adalah m:n; Perbandingan posisi luar adalah m:-n

Contoh Soal dan Jawaban Perkalian Vektor

1. Dua buah vektor pangkalnya saling bertemu membentuk sudut 60°, vektor A panjangnya 60 cm sedangkan vektor B panjangnya 40 cm. Berapa nilai perkalian titik (dot) dan perkalian silang (cross) kedua vektor tersebut?

Jawaban:

Perkalian titik, yaitu

Perkalian silang, yaitu

2. Sebuah hasil perkalian vektor diperoleh bahwa A.B = 40 meterpersegi. Jika besar vektor B yang panjangnya 4 meter membentuk sudut 60°. Berapa panjang vektor A dalam centimeter?

Jawaban:

Dengan menggunakan rumus perkalian titik (dot product), maka diperoleh perhitungan sebagai berikut.

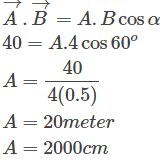
3. Tentukan Kedua Vektor di bawah ini.

Tentukanlah besar sudut yang dibentuk oleh kedua vektor tersebut.

Solusi :

A.B = |A||B| cos ⁡ α

Sebelum kita mencari besar sudut yang dibentuk maka terlebih dahulu kita mencari besar atau panjang dari kedua vektor dan Perkalian Dot dari Kedua Vektor tersebut

*Panjang Vektor

Konsep Perkalian Titik (Dot Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan

*Perkalian Dot

Setelah kita mendapatkan Panjang Vektor dan Hasil Perkalian Dot kedua vektor maka dengan mudah kita mengetahui sudut yang dibentuk oleh kedua vektor tersebut.

Jadi, besar sudut yang terbentuk oleh dua vektor tersebut adalah 4,88 drajat.

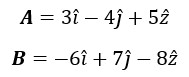
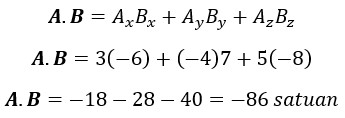
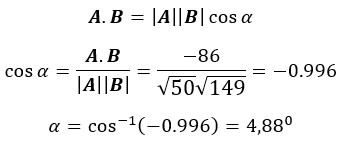
**4. Dua buah vektor A dan B pangkalnya membentuk sudut 60°. Jika A = 2 Bdan A.B=400 meterpersegi. Maka berapa besar vektor A dan B?**

Jawaban:

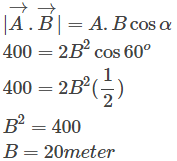
Setelah besar vektor B diketahui, maka A = 2.20 = 40 meter.

5. Vektor A memiliki panjang sebesar 10 cm sedangkan vektor B memiliki panjang sebesar 20 cm. Keduanya memiliki pangkal yang membentuk sudut a. Jika A x B besarnya 1 meterpersegi, berapa besar sudut a?

Jawaban:

Terlebih dahulu kita samakan satuannya, A x B = 1 meter = 100 centimeterpersegi. Kemudian dengan menggunakan rumus perkalian silang, kita peroleh…

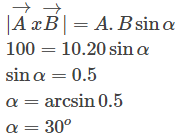
6. Tentukan Hasil perkalian Titik (Dot Product) dari dua Vektor Berikut Ini

Solusi:

Jadi perkalian dari dua vektor tersebut adalah -56 Satuan. Yang mana satuannya tergantung dari besaran vektor yang dikalikan. Misalnya kita mengalikan vektor gaya dan perpindahan, maka satuannya adalah Nm.

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Tentang Matematika

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita! Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math is Fun

Perkalian Vektor: Produk Skalar / Perkalian Titik, Silang dan Langsung – Bersama Contoh Soal dan Jawaban

Perkalian Vektor

Produk Skalar Vektor atau Perkalian Titik

Perkalian Silang Vektor

Perkalian langsung Vektor

Produk Skalar / Perkalian Titik

Definisi menurut aljabar

Definisi menurut geometri

Sifat Produk Skalar / Perkalian Titik

Posisi vektor

Panjang vektor

Vektor satuan

Operasi aljabar pada vektor

Sifat operasi aljabar pada vektor

Hubungan vektor dengan vektor lain

Sudut dua vektor

Panjang proyeksi dan proyeksi vektor

Perbandingan

Contoh Soal dan Jawaban Perkalian Vektor

1. Dua buah vektor pangkalnya saling bertemu membentuk sudut 60°, vektor A panjangnya 60 cm sedangkan vektor B panjangnya 40 cm. Berapa nilai perkalian titik (dot) dan perkalian silang (cross) kedua vektor tersebut?

2. Sebuah hasil perkalian vektor diperoleh bahwa A.B = 40 meterpersegi. Jika besar vektor B yang panjangnya 4 meter membentuk sudut 60°. Berapa panjang vektor A dalam centimeter?

3. Tentukan Kedua Vektor di bawah ini.

**4. Dua buah vektor A dan B pangkalnya membentuk sudut 60°. Jika A = 2 Bdan A.B=400 meterpersegi. Maka berapa besar vektor A dan B?**

5. Vektor A memiliki panjang sebesar 10 cm sedangkan vektor B memiliki panjang sebesar 20 cm. Keduanya memiliki pangkal yang membentuk sudut a. Jika A x B besarnya 1 meterpersegi, berapa besar sudut a?

6. Tentukan Hasil perkalian Titik (Dot Product) dari dua Vektor Berikut Ini

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Tentang Matematika

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan