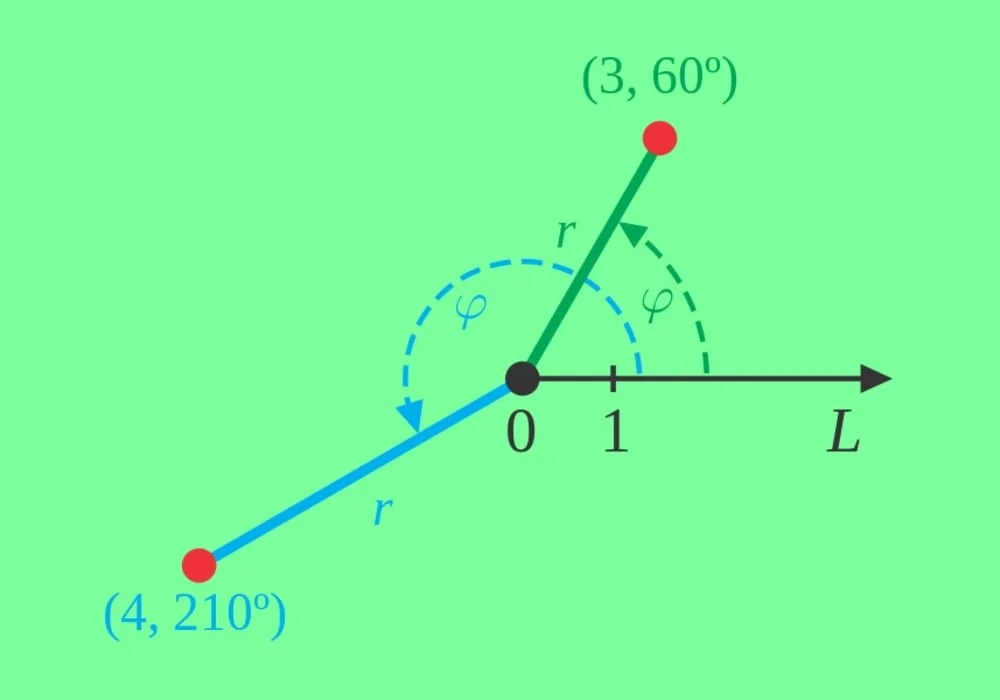
Penjelasan Koordinat Polar
Sistem koordinat polar (sistem koordinat kutub) dalam matematika adalah suatu sistem koordinat 2-dimensi di mana setiap titik pada bidang ditentukan dengan jarak dari suatu titik yang telah ditetapkan dan suatu sudut dari suatu arah yang telah ditetapkan.
Sistem koordinat polar (sistem koordinat kutub)
Dalam matematika adalah suatu sistem koordinat 2-dimensi di mana setiap titik pada bidang ditentukan dengan jarak dari suatu titik yang telah ditetapkan dan suatu sudut dari suatu arah yang telah ditetapkan.
Titik yang telah ditetapkan (analog dengan titik origin dalam sistem koordinat Kartesius) disebut pole atau “kutub”, dan ray atau garis geometri “sinar” dari kutub pada arah yang telah ditetapkan disebut “aksis polar” (polar axis). Jarak dari suatu kutub disebut radial coordinate atau radius, dan sudutnya disebut angular coordinate, polar angle, atau azimuth.
Konversi dari atau ke koordinat Kartesius
Contoh sebuah diagram menggambarkan hubungan antara sistem koordinat Kartesius dan polar.
Sebuah kurva dalam bidang Kartesian dapat dipetakan ke dalam koordinat polar. Dalam animasi ini, dipetakan kepada .
Koordinat polar r dan φ dapat dikonversi ke dalam sistem koordinat Kartesius x dan y menggunakan fungsi trigonometri sinus dan kosinus:
Koordinat Kartesian x dan y dapat dikonversi ke dalam koordinat polar r dan φ dengan r ≥ 0 dan φ dalam interval (−π, π] dengan:
- (sebagaimana dalam teorema Pythagoras atau Euclidean norm), dan
- ,
di mana atan-antan merupakan variasi umum pada fungsi arctangent yang didefinisikan sebagai:
Nilai φ di atas adalah principal value dari fungsi bilangan kompleks argument yang diterapkan pada x+iy. Suatu sudut dalam rentang [0, 2π) dapat diperoleh dengan menambahkan 2π pada nilai sudut itu jika nilainya negatif.
Sejarah Sistem Koordinat Polar
Dari abad ke-8 M dan seterusnya, para astronom mengembangkan metode untuk menghitung arah ke Mekkah (kiblat)— dan jaraknya — dari semua lokasi di bumi.
Kaidah Sistem Koordinat Polar
Sebuah grid polar dengan beberapa sudut yang diberi label dalam derajat.
Koordinat radial
Koordinat radial sering dilambangkan dengan r, dan koordinat angular dilambangkan dengan φ, θ, atau t. Koordinat angular ditetapkan sebagai φ oleh standar ISO 31-11.
Sudut dalam notasi polar
Sudut dalam notasi polar biasanya dinyatakan dalam derajat atau radian (2π rad sama dengan to 360°). Derajat biasanya digunakan dalam navigasi, surveying, dan banyak bidang, sementara radian lebih umum dalam matematika dan fisika.
Dalam banyak konteks, suatu koordinat angular positif berarti sudut φ diukur berlawanan dengan jarum jam dari aksis.
Dalam literatur matematika, aksis polar sering digambar horizontal dan mengarah ke kanan.
Contoh Soal dan Jawaban Koordinat Polar (sistem koordinat kutub)
1. Mengubah atau Mengkonversi Koordinat Polar ke Koordinat Kartesius. Koordinat kartesius dari titik (10, 315°) adalah…
A. (-5, -5√2)
B. (-5, 5√2)
C. (5√2, 5√2)
D. (5√2, -5√2)
E. (5, -5√2)
Jawab : D
» Sudut 315° (kuadran IV) —–> (x, -y)
» Dari pilihan jawaban di atas maka kemungkinan jawabannya D atau E
» (r, α) ——> (10, 315°)
x = 10 . cos 315°
x = 10 . ½√2
x = 5√2
y = 10 . sin 315°
y = 10 . -½√2
y = -5√2
Jadi koordinat kartesiusnya adalah (5√2, -5√2)
Untuk lebih jelas dapat dilihat pada gambar di samping.
2. Mengubah atau Mengkonversi Koordinat Kartesius ke Koordinat Polar. Koordinat kutup dari titik (-6, 6√3) adalah…
A. (12, 30°)
B. (12, 60°)
C. (12, 90°)
D. (12, 120°)
E. (12, 210°)
Jawab : D
Cara biasa
r² = (-6)² + (6√3)²
r² = 36 + 108
r² = 144
r = 12
a = arc tan (6√3) / -6
a = arc tan -√3
a = 120°
Jadi koordinat kutubnya adalah (12, 120°)
Cara praktis
» (-6, 6√3) ——-> (-x, y) —–> maka berada di kuadran II
» Dari pilihan jawaban di atas yang berada di kuadran II yaitu hanya pilihan D
» Sedangkan r tidak usah dicari karena dari pilihan jawaban semuanya sama.
3. Untuk koordinat kartesius ke koordinat kutub koordinat kutub titik (-4,4) adalah…
penyelesaian :
(x,y)⇒ (r, α)
x = -4, y=4
(karena x negatif dan y positif, maka α sudut di kuadran II)
r =
⇒
⇒
⇒
tan α = x/y
⇒4/ – 4
⇒ – 1
karena α sudut di kuadran II, maka : α = (180-45)°= 135°
maka koordinat kutubnya ialah ( 4√2, 135°)
4. Untuk koordinat kutub ke koordinat kartesius
Jika diketahui koordinat kutub (6√3, 60°), maka koordinat kartesiusnya adalah…
a. (3,3)
b. (3√3, 9)
c. (3, √3)
d. (9, 3√3)
e. (3, 3√3)
Penyelesaian :
koordinat kutub ⇒ koordinat kartesius
(r , α) ⇒ ( x , y )
r = 6√3 ; α = 60°
(Karena α sudut di kuadran I, maka x positif f dan y positif)
x = r cos α
⇒ 6√3 x cos 60°
⇒ 6√3 x 1/2
⇒ 3√3
y = r sin α
⇒ 6√3 x sin 60°
⇒ 6√3 x 1/2 √3
⇒ 3 x 3
⇒ 9
sehingga koordinat kartesiusnya ialah ( 3√3 , 9) (d)
Bacaan Lainnya
- Induksi Elektromagnetik – Hukum Faraday dan Hukum Lenz – Soal dan Jawaban
- Induksi dan Fluks Magnetik Bersama Contoh Soal dan Jawaban
- Rumus Rangkaian Listrik Dan Contoh-Contoh Soal Beserta Jawabannya
- Tabel Konstanta Fisika – Tabel konstanta universal, elektromagnetik, atom dan nuklir, fisika-kimia, nilai yang diadopsi, satuan natural, bilangan tetap
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
- Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
- Cara Menghentikan Penindasan Bullying
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Apakah Produk Pembalut Wanita Aman?
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Lumen Learning, Math is Fun
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing
Penjelasan koordinat polar ini padat, lengkap dan mudah di mengerti.
Padat-ringkas dan exelent bagi senior bagi junior