Konduksi Panas

Konduksi panas atau konduksi termal adalah penjalaran kalor tanpa disertai perpindahan bagian-bagian zat perantaranya.

Rumus Konduksi

Q ∆t = H = k.A

H = Jumlah kalor merambat setiap detik (J/s)
k = Koefisien konduksi termal (J/msK)
A = luas penampang pada batang (m)
L = Panjang pada Batang (m)
∆ T = perbedaan suhu di kedua ujung batang (K)

Dinding yang berbentuk geometri sederhana

Dinding datar

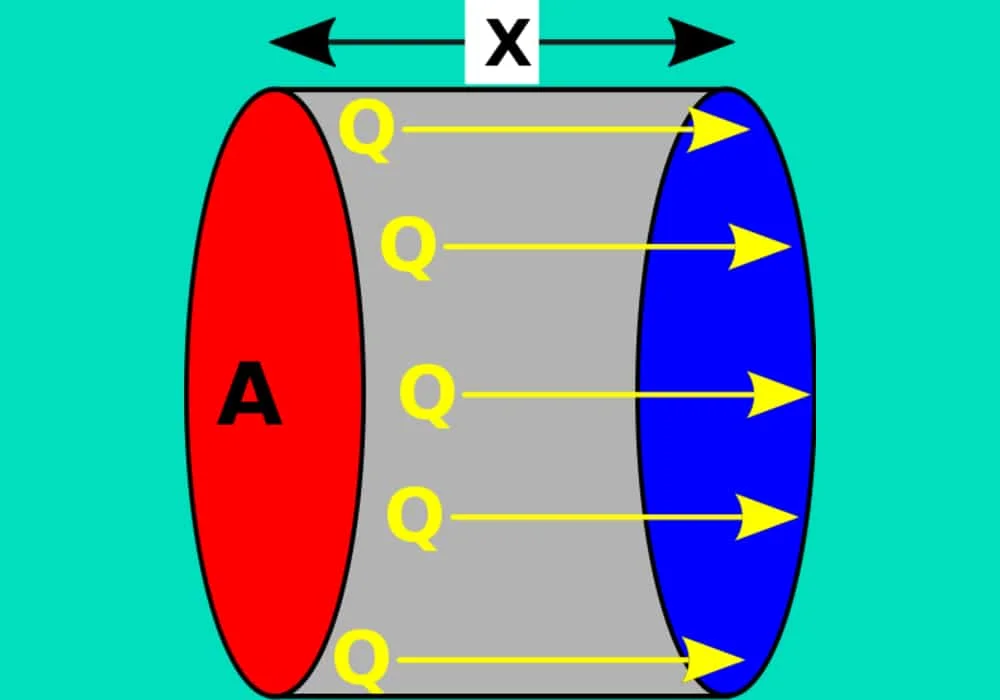
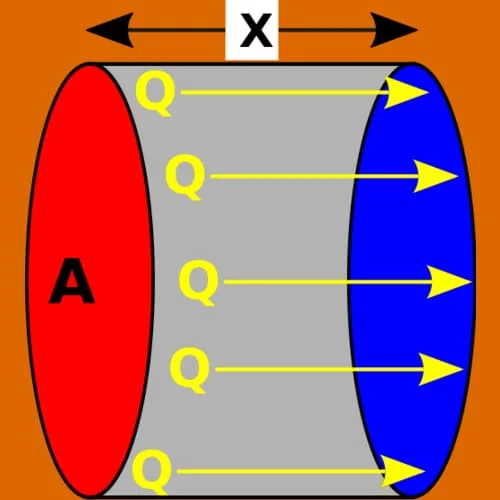
Aliran panas satu dimensi yang terjadi pada dinding datar dengan distribusi temperatur yang seragam melalui suatu bahan yang homogen, dihitung melalui persamaan :

q_k = k * A * (T_panas-T_dingin)/ x

q_k = K_k * ΔT

q_k = ΔT/ R_k

Keterangan :

q_k = laju aliran panas konduksi, (W)
k = koefisien perpindahan panas konduksi, (W/mK)
T_panas = temperatur tinggi, (K)
T_dingin = temperatur rendah, (K)
A = luas penampang, (m²)
ΔT = beda temperatur, (K)
x = tebal bahan, (m)
K_k = Konduktansi termal konduksi, (W/K)
R_k = tahanan termal konduksi, (K/W)

Silinder berlubang

Aliran panas radial dengan cara konduksi melalui silinder berpenampang lingkaran yang berlubang, misalnya konduksi pada pipa atau isolasi pipa, dihitung melalui persamaan :

q_k = k * A * (dT/dr)

q_k = (2 π k L) * (T_i– T_o)/ ln (r_o/r_i)

q_k = k * A~ * (T_i– T_o)/ (r_o– r_i)

Keterangan :

L = panjang silinder, (m)
T_i = temperatur bagian dalam, (K)
T_o = temperatur bagian luar, (K)
r_i = jari-jari luas bagian dalam, (m)
r_o = jari-jari luas bagian luar, (m)
A~ = luas rata-rata logaritmik, (m²)
A~= (2 π L) * (r_o– r_i)/ ln (r_o/r_i)
A~ = (A_o – A_i) / ln (A_o / A_i)

Keterangan :

A_i = luas silinder bagian dalam, (m²)
A_o = luas silinder bagian luar, (m²)

Cangkang yang berbentuk bola dan paralepipeda

Konduksi panas melalui bola dengan temperatur permukaan dalam dan luarnya seragam dan konstan, dihitung melalui persamaan:

q_k = (4 π r_i * r_o * k) * (T_i– T_o)/ (r_o– r_i)

q_k = k * (A_o – A_i)^1/2 * (T_i– T_o)/ (r_o– r_i)

Pengaruh Konduktivitas termal yang tak seragam

Beberapa kasus diatas diandaikan bahwa pengaruh perubahan temperatur tidak terlalu besar sehingga pengaruh temperatur terhadap konduktivitas termal diabaikan. Untuk beberapa bahan, pengaruh perubahan temperatur terhadap konduktivitas termal sangat besar, dihitung melalui persamaan :

k_t = k_o* (1+ _kT)

Keterangan :

k_t = koefisien perpan konduksi pada T_t, (W/mK)
k_o = koefisien perpan konduksi pada T_o, (W/mK)
_k = koefisien temperatur konduktivitas termal, (K^-1)

Dengan memperhatikan faktor diatas, laju aliran panas konduksi,

q_k = k_o * A * ((T_p– T_d) + _k/2 (T_p²– T_d²))/x
q_k = k_o * A * ((T_p– T_d) + (1 + _k (T_p– T_d) /2)/x
q_k = k_m * A * ΔT / L

Dengan :

k_m = k_o * (1 + _k (T_p– T_d) /2)

Struktur komposit

Dinding Komposit

Dengan asumsi bahwa pada tiap-tiap dinding ini laju aliran panas besarnya sama, sehingga:

q = h₁* A * (T_i-T₁) = k * A * ΔT /x

Bila persamaan diatas diganti dengan konsep tahanan termal, diperoleh :

q = (T_i-T₁) /R₁ = (T₁-T₂) /R₂ = (T₂-T₃) /R₃ = (T₃-T₄) /R₄ = (T₄-T_o) /R₅

atau :

(T_i-T₁) = q * R₁; (T₁-T₂) = q * R₂ ; (T₂-T₃) = q * R₃ ; (T₃-T₄) = q * R₄ ; (T₄-T_o) = q * R₅

Sehingga :

(T_i-T_o) = q * (R₁+R₂ + R₃ + R₄ + R₅)

Atau, laju aliran panas yang mengalir,

q = (T_i-T_o) /(R₁+R₂ + R₃ + R₄ + R₅)

Konduksi Panas dan Hukum Fourier - Rumus, Contoh Soal dan Jawaban — Diagram yang menunjukkan aliran panas dari panas ke dingin, untuk menggambarkan Hukum konduksi panas (hukum Fourier), bila diintegrasikan. Artikel: Konduksi Panas dan Hukum Fourier – Rumus, Contoh Soal dan Jawaban. Sumber foto: Wikimedia Commons

Contoh Konduksi Panas

Berikut adalah beberapa contoh proses konduksi kalor:

Ketika berjalan di luar tanpa alas kaki siang hari, panas dari aspal berpindah secara konduksi ke kakinya.
Balok es diletakkan di tangan kita. Seiring waktu, panas berpindah secara konduksi dari tangan pria itu ke es batu akan menyebabkan es mencair.
Mesin mobil dihidupkan, dan kap mobil menjadi hangat karena konduksi panas dari mesin ke kap mobil secara konduksi.
Seorang anak laki-laki dipeluk ibunya menjadi hangat. Ini karena panas dipindahkan secara konduksi dari tubuh ibunya ke tubuhnya sendiri melalui proses konduksi.
Wajan besi dingin diletakkan di atas kompor. Ketika kompor dihidupkan, wajan menjadi sangat panas karena konduksi panas dari kompor ke wajan.
Kemeja ditempatkan di papan setrika untuk disetrika. Panas dari setrika bepindah secara konduksi ke baju, membuatnya mudah untuk menghilangkan semua kerutan yang tidak sedap dipandang dan membuat kemeja terlihat tajam.
Seorang anak laki-laki mengambil satu sen dari meja, dan itu terasa sangat dingin saat disentuh. Setelah memegangnya selama beberapa detik, panas dari tangannya secara konduksi ke koin logam.
Radiator dihidupkan untuk menghangatkan rumah pada hari yang dingin, dan pemilik rumah meletakkan topinya di atasnya. Topi menjadi lebih hangat karena radiator menghantarkan panas secara konduksi padanya.

Hukum Fourier

Hukum konduksi panas, disebut juga Hukum Fourier, menyatakan bahwa tingkat (rate) perpindahan panas melalui sebuah material adalah berbanding lurus dengan gradien negatif pada suhu dan luas, pada sudut siku pada gradien tersebut, melalui dimana panas mengalir.

Hukum Fourier dapat dinyatakan dalam 2 bentuk ekivalen:

1. Bentuk diferensial, dimana dilihat dari laju alir atau fluks energi secara lokal.

2. Bentuk integral, dimana dilihat dari jumlah energi yang mengalir dari dan ke sebuah sistem secara keseluruhan,

Bentuk diferensial

Bentuk diferensial Hukum Fourier tentang konduksi panas menyatakan bahwa rapat fluks panas lokal, ${\overrightarrow {q}}$ , sama dengan perkalian antara konduktivitas panas, $k}$ dengan negatif gradien suhu lokal, $-\nabla T$ . Rapat fluks panas adalah jumlah energi yang mengalir melalui sebuah satuan luas per satuan waktu.

{\overrightarrow {q}}=-k{\nabla }T

dimana (termasuk satuan SI)

{\overrightarrow {q}}

adalah rapat fluks panas lokal, W·m⁻²

{\big .}k{\big .}

adalah konduktivitas panas bahan, W·m⁻¹·K⁻¹,

{\big .}\nabla T{\big .}

adalah gradien suhu, K·m⁻¹.

Konduktivitas panas, $k$ , sering dianggap konstan meski hal ini tidak selalu benar. Ketika konduktivitas panas bahan umumnya bervariasi menurut temperatur, perbedaannya sering kali kecil untuk selang suhu yang besar pada beberapa material umum. Pada material anisotropi, konduktivitas panas umumnya berbeda menurut orientasi, dalam kasusu ini $k$ dinyatakan dengan tensor orde-dua. Untuk material non-uniform, $k$ bervariasi menurut lokasi spasial.

Untuk banyak aplikasi sederhana, hukum Fourier digunakan dalam bentuk satu dimensinya. Dalam arah-x,

q_{x}=-k{\frac {dT}{dx}}

Bentuk integral

Dengan mengintegralkan bentuk diferensial terhadap total permukaan bahan $S$ , didapatkan bentuk integral Hukum Fourier:

{\frac {\partial Q}{\partial t}}=-k

$\oiint$

{\nabla }T\cdot \,dS

dimana (termasuk satuan SI):

${\big .}{\frac {\partial Q}{\partial t}}{\big .}$ adalah jumlah panas berpindah per satuan waktu (dalam W), dan
$dS$ adalah elemen luas permukaan (dalam m²)

Persamaan diferensial diatas, jika diintegralkan untuk material homogen geometri satu bidang antara 2 titik pada suhu konstan, menghasilkan laju alir panas sebagai:

{\big .}{\frac {\Delta Q}{\Delta t}}=-kA{\frac {\Delta T}{\Delta x}}

dengan

A adalah luas permukaan cross-sectional,

\Delta T

adalah beda temperatur antara kedua ujung,

\Delta x

adalah jarak antara kedua ujung.

Hukum ini membentuk dasar bagi penurunan persamaan panas.

Contoh Soal + Jawaban Konduksi Panas

Sebuah batang logam mempunyai panjang 2 m, dan memiliki luas penampang 20 cm²dan perbedaan suhu kedua ujungnya 50⁰C. Bila koefisien konduksi termalnya 0,2 kal/ms⁰C, tentukan jumlah kalor yang merambat per satuan luas & per satuan waktu!

Diketahui :

L = 2 m
A = 20 cm²= 2 x 10^-3m²k = 0,2 kal/ms⁰C
∆ T = 50⁰C
Pertanyaan: H

Jawaban:

H = k A ∆ T/L
= (0,2 kal/ms⁰C)(2 x 10^-3m²) 50⁰C/2 m
= 0,01 kal/s

Batang besi dengan panjang 4 m, memiliki luas penampang 24 cm², dan perbedaan suhu kedua ujungnya 50º C. Jika koefisien konduksi termalnya 0,2 kal/msC. Tentukan jumlah kalor yang dirambatkan!

Solusi:

Diketahui:

L = 4 m
A = 24 cm² = 0,00024 m² = 24 × 10^-4 m²k = 0,2 kal/msK
ΔT = 50º C

Ditanya: H = … ?

Jawab:

H = (k . A . ΔT)/L
H = (0,2 . 24 × 10^-4 . 50)/4
H = 0,0024/4
H = 0,0006
H = 6 × 10^-4J/s

Jadi, jumlah kalor yang dirambatkan oleh besi yang dipanaskan adalah 6 × 10^-4J/s.

Faktor-faktor yang tidak memengaruhi laju perpindahan kalor secara konduksi pada sebuah logam adalah…

A. panjang penghantar
B. luas penampang
C. emisivitas
D. perbedaan suhu
E. konduktivitas termal

Pembahasaan :
Emisivitas tidak mempengaruhi laju perpindahan kalor secara konduksi.

Jawaban : C

Suatu batang logam yang salah satu ujungnya dipanasi. Batang logam tersebut memiliki luas penampang 25 cm²dan konduktifitas termal 4.10⁵ J/smC. Panjang batang logam tersebut 8 m dan perbedaan suhu kedua ujungnya 30º C. Kalor yang merambat dalam batang besi selama 2 detik adalah…

Solusi:

Diketahui:
A = 25 m²k = 4 × 10⁵ J/msC
L = 8 m
ΔT = 30º C
t = 2 s

Ditanya: Q = … ?

Jawab:
Q = (k . A . t) . ΔT/L
Q = (4 × 10⁵. 25 . 2) 30/8
Q = 75 × 10⁶ J

Jadi, kalor yang merambat pada batang besi adalah 75 × 10⁶ J.

3. Dua batang aluminium A dan B memiliki perbandingan luas penampang 3:2. Sedangkan perbandingan panjangnya 5:4. Jika perbedaan suhu ujung kedua aluminium sama. Rambatan kalor tiap satuan waktu pada aluminium A dan B adalah…

Solusi:

Diketahui:

Perbandingan luas penampang aluminium A dan B = 3:2
Perbandingan panjang aluminium A dan B = 5:4

Ditanya: Rambatan kalor pada aluminium A dan B?

Jawab:

ΔT_A = ΔT_B(Q_A . L_A)/k_A . A_A . t_A = (Q_B . L_B /k_B . A_B . t_B(Q_A . 5)/k_A . 3 . t_A = (Q_B . 4)/k_B . 2 . t_B(Q_A/k_A ) 5/3 = (Q_B/k_B)/4/2
(Q_A/k_A )/(Q_B/k_B) = (4/2)/(5/3)
(Q_A/k_A )/(Q_B/k_B) = (4/2) × (3/5)
(Q_A/k_A )/(Q_B/k_B) = 12/10
(Q_A/k_A )/(Q_B/k_B) = 0,12 J

Jadi, rambatan kalor pada aluminium A dan B adalah 0,12 J.

Contoh soal silinder berlubang. Pipa dengan jari-jari 40 mm dan panjang 4 m yang diberi lapisan isolasi setebal 4 cm dengan koefisien perpan, k = 0,744 W/mK memiliki temperatur 20^°C dan 30^°C, tentukan laju aliran panas yang terjadi!

Diketahui : temperatur, T₁ = 30^°C= 303 K, T₂ = 20^°C = 293 K; tebal, x = 4 cm = 4 * 10^-2 m; koefisien perpan, k = 0,744 W/mK; jari-jari, r = 40 mm = 4 * 10^-2 m, panjang, L = 4 m

Diminta : laju aliran panas yang terjadi

Jawab :

Panas yang berpindah dari satu sisi ke sisi lainnya pada dinding Pipa, terjadi dengan cara konduksi, menurut J.B.J Fourier, untuk perpindahan panas dengan cara konduksi, berlaku persamaan :

q_k = k * A~ * (T_i– T_o)/ (r_o– r_i)

dengan :

A~= (2 π L) * (r_o– r_i)/ ln (r_o/r_i)
A~= (2 * π * 4 (m)) * (0,008– 0,004) (m)/ ln (0,008/0,004) (m/m)
A~= (2 * π * 4 (m)) * (0,008– 0,004) (m)/ ln (0,008/0,004) (m/m)
A~= 1,45 m²

Sehingga, laju aliran panas yang terjadi,

q_k = 0,744 (W/mK) * 1,45 (m²) (303 -293) (K)/ (0,008– 0,004) (m)
q_k = 270,27 W

Lempengan tembaga mempunyai luas penampang 25 cm² panjang 55 cm. Jika perubahan suhu kedua ujungnya 50º C dan konduktifitas kalor dari tembaga adalah 0,16 W/mK. Berapa laju perpindahan kalor?

Solusi:

Diketahui:

A = 25 cm² = 25 × 10^-4 m²L = 55 cm = 55 × 10^-2 m
ΔT = 50º C = 323,15 K
k = 0,16 W/mK

Ditanya: H = … ?

Jawab:

H = Q/t = (k . A . ΔT)/L
H = Q/t = (0,16 . 25 × 10^-4 . 323,15)/55 × 10^-2H = Q/t = 0,002/55 × 10^-2H = Q/t = 0,036
H = Q/t = 36 × 10^-2J/s

Jadi, laju perpindahan kalor adalah 36 × 10^-2J/s.

Soal dinding datar. Dinding sebuah gudang memiliki temperatur 23^°C pada bagian dalam dan 30^°C pada bagian luar dengan koefisien perpan dinding, k = 2,69 W/mK serta tebal dinding 15 cm, tentukan laju aliran panas/ satuan luas yang terjadi !

Diketahui : temperatur dinding, T₁ = 30^°C= 303 K, T₂ = 23^°C = 296 K; tebal, x = 15 cm = 15 * 10^-2 m; koefisien perpan dinding, k = 2,69 W/mK

Diminta : laju aliran panas/ satuan luas yang terjadi

Jawab :

Panas yang berpindah dari satu sisi ke sisi lainnya benda padat, terjadi dengan cara konduksi, menurut J.B.J Fourier, untuk perpindahan panas dengan cara konduksi, berlaku persamaan :

q_k = k * (A/x) * (T_panas-T_dingin)

atau, untuk laju aliran panas/ satuan luas

q_k /A = k * (T_panas-T_dingin) /x
q_k /A = 2,69 (W/mK) * (303 -296) (K)/ 15 * 10^-2 (m)
q_k /A = 125,5 W/ m

Soal dinding datar. Ruang kerja sebuah ruangan di laboratorium memiliki ukuran 6 * 8 * 12 m³ dengan tebal dinding 15 cm dan dipanaskan dengan energi listrik. Bila dinding terbuat dari bata tahan api, k = 1,09 W/mK dimana temperaturnya dipertahankan 1100^°C pada bagian dalam dan 200^°C pada bagian luar, tentukan laju aliran panas yang melewati dinding tersebut !

Diketahui: temperatur dinding, T₁ = 1100^°C= 1373 K; temperatur sekeliling, T₂ = 200^°C = 473 K; tebal, x = 15 cm = 15 * 10^-2 m; koefisien perpan bata tahan api, k = 1,09 W/mK

Diminta : laju aliran panas yang melewati dinding tersebut

Jawaban:

Panas yang berpindah dari satu sisi ke sisi lainnya pada dinding bata, terjadi dengan cara konduksi, menurut J.B.J Fourier, untuk perpindahan panas dengan cara konduksi, berlaku persamaan:

q_k = k * (A/x) * (T_panas-T_dingin)
q_k = 1,09 (W/mK) * 432 (m²) (1373 -473) (K)/ 15 * 10^-2 (m)
q_k = 2825280 W

Dua batang besi X dan Y disambungkan pada salah satu ujungnya. Pada ujung-ujung yang lain diberi panas sengan suhu berbeda, 60º C dan 30º C. Jika panjang logam sama dan konduktifitas besi X dua kali lipat besi Y. Tentukan suhu pada sambungan kedua logam!

Solusi:

Diketahui:

T_X= 60º C
T_Y = 30º C
L_X = L_YA_X = A_YK_X = k_X

Ditanya: T = … ?

H_X = H_Y(k_X . A_X . ΔT_X)/L_X = (k_Y . A_Y . ΔT_Y)/L_Yk_X. ΔT_X = k_Y . ΔT_Y2 k_Y. (60º – T) = k_Y . (T – 30º)
2 . (60º – T) = (T – 30º)
120º – 2T = T – 30º
120º + 30º = T + 2T
150º = 3T
150º/3 = T

50º = T Jadi, suhu pada sambungan kedua logam adalah 50º C.

Lempengan tembaga yang dipanaskan salah satu ujungnya memiliki panjang 4 m dan lebarnya 2 m. suhu masing-masing ujung tembaga adalah 33º C dan 43º C. Konduksi termal tembaga adalah 8 × 10^-1 W/mK. Berapa jumlah kalor yang mengalir?

Solusi:

Diketahui:

L = 4 m
l = 2 m
T₁= 33º C = 306,15 K
T₂ = 43º C = 316,16 K
k = 8 × 10^-1 W/mK

Ditanya: H= … ?

Jawab:

A = L × l = 4 × 2 = 8 m²ΔT = T₂ – T₁ = 316,16 – 306,15 = 10º K
H = Q/t = (k . A . ΔT)/L
H = Q/t = (8 × 10^-1 . 8 . 10)/4
H = Q/t = 8 × 10^-1 . 2 . 10
H = Q/t = 16 Watt

Jadi, jumlah kalor yang mengalir adalah 16 Watt.

Contoh soal dinding Komposit. Dinding sebuah tanur terdiri dari 3 lapisan, yaitu : bata tahan api, k_bta = 0,8 Btu/hr ft^°F; isolasi, k_i = 0,1 Btu/hr ft^°F; dan bata merah, k_bm = 0,58 Btu/hr ft^°F dimana temperaturnya dipertahankan 3000^°F pada bagian dalam dan 80^°F pada bagian luar dan memiliki luas, A = 60 ft², tentukan laju aliran panas yang melewati dinding tanur tersebut.

Diketahui : temperatur dinding, T_p = 3000^°F, T_c = 80^°F; tebal, x_bta = ¾ ft, x_i = 1/3 ft, x_bm = 1/2 ft ; koefisien perpan dinding, k_bta = 0,8 Btu/hr ft^°F, k_i = 0,1 Btu/hr ft^°F, k_bm = 0,58 Btu/hr ft^°F ; luas, A = 60 ft²

Diminta: laju aliran panas yang melewati dinding tersebut

Jawaban:

Laju aliran panas yang melewati dinding tersebut, dihitung dengan persamaan :

q_tot = ΔT / R_tot

q_tot = (T_p-T_c) / /(R_sp+R_bta + R_i + R_bm + R_sc)

Dengan :

R_sp = 1 / (h_p* A)
R_sp = 1 / (12 (Btu/hrft^2°F)* 60 (ft²))
R_sp = 0,00139 hr^°F/ Btu
R_bta = x_bta / (k_bta* A)
R_bta = ¾ (ft) / (0,8 (Btu/hrft^°F)* 60 (ft²))
R_bta = 0,0156 hr^°F/ Btu
R_i = x_i / (k_i* A)
R_i = 1/3 (ft) / (0,1 (Btu/hrft^°F)* 60 (ft²))
R_i = 0,0556 hr^°F/ Btu
R_bm = x_bm / (k_bm* A)
R_bm = 1/2 (ft) / (0,58 (Btu/hrft^oF)* 60 (ft²))
R_bm = 0,0144 hr^oF/ Btu
R_sc = 1 / (h_c* A)
R_sc = 1 / (2 (Btu/hrft^2oF)* 60 (ft²))
R_sc = 0,00833 hr^°F/ Btu

Sehingga, Laju aliran panas yang melewati dinding tersebut

q_tot = (3000-80)(^oF)/( 0,00139+0,0156 + 0,0556 + 0,0144 + 0,00833 )(hr^oF/ Bt)

q_tot = 30633,66 Btu/hr)

Contoh soal dinding Komposit. Sebatang tembaga murni dengan panjang 100 cm dipanaskan hingga mencapai temperatur 300^°C. Bila lebar tembaga 100 cm dan tebalnya 1 cm, tentukan panas yang berpindah bila temperatur sekelilingnya 50^Oc dengan koefisien perpan tembaga, k = 369 W/mK!

Diketahui : temperatur tembaga, T₁ = 300^°C = 573 K; temperatur sekeliling, T₂ = 50^°C = 323 K; panjang, L = 100 cm = 1 m; tebal, x = 1 cm = 10^-2 m; koefisien perpan tembaga, k = 369 W/mK

Diminta: panas yang berpindah

Jawaban:

Panas yang berpindah dari satu sisi ke sisi lainnya benda padat, terjadi dengan cara konduksi, menurut J.B.J Fourier, untuk perpindahan panas dengan cara konduksi, berlaku persamaan :

q_k = k * (A/x) * (T_panas-T_dingin)

q_k = 369 (W/mK) * (1 * 1 (m²) /10^-2 (m)) * (573 -323) (K)

q_k = 9225 kW

Rumus Fisika Lainnya

Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Colorado State University, Science Direct, Machine Design

Konduksi Panas dan Hukum Fourier – Rumus, Contoh Soal dan Jawaban

Konduksi Panas

Rumus Konduksi

Dinding yang berbentuk geometri sederhana

Silinder berlubang

Cangkang yang berbentuk bola dan paralepipeda

Pengaruh Konduktivitas termal yang tak seragam

Struktur komposit

Contoh Konduksi Panas

Hukum Fourier

Hukum Fourier dapat dinyatakan dalam 2 bentuk ekivalen:

Bentuk diferensial

Bentuk integral

Contoh Soal + Jawaban Konduksi Panas

Sebuah batang logam mempunyai panjang 2 m, dan memiliki luas penampang 20 cm²dan perbedaan suhu kedua ujungnya 50⁰C. Bila koefisien konduksi termalnya 0,2 kal/ms⁰C, tentukan jumlah kalor yang merambat per satuan luas & per satuan waktu!

Batang besi dengan panjang 4 m, memiliki luas penampang 24 cm², dan perbedaan suhu kedua ujungnya 50º C. Jika koefisien konduksi termalnya 0,2 kal/msC. Tentukan jumlah kalor yang dirambatkan!

Faktor-faktor yang tidak memengaruhi laju perpindahan kalor secara konduksi pada sebuah logam adalah…

Suatu batang logam yang salah satu ujungnya dipanasi. Batang logam tersebut memiliki luas penampang 25 cm²dan konduktifitas termal 4.10⁵ J/smC. Panjang batang logam tersebut 8 m dan perbedaan suhu kedua ujungnya 30º C. Kalor yang merambat dalam batang besi selama 2 detik adalah…

Contoh soal silinder berlubang. Pipa dengan jari-jari 40 mm dan panjang 4 m yang diberi lapisan isolasi setebal 4 cm dengan koefisien perpan, k = 0,744 W/mK memiliki temperatur 20^°C dan 30^°C, tentukan laju aliran panas yang terjadi!

Lempengan tembaga mempunyai luas penampang 25 cm² panjang 55 cm. Jika perubahan suhu kedua ujungnya 50º C dan konduktifitas kalor dari tembaga adalah 0,16 W/mK. Berapa laju perpindahan kalor?

Soal dinding datar. Dinding sebuah gudang memiliki temperatur 23^°C pada bagian dalam dan 30^°C pada bagian luar dengan koefisien perpan dinding, k = 2,69 W/mK serta tebal dinding 15 cm, tentukan laju aliran panas/ satuan luas yang terjadi !

Dua batang besi X dan Y disambungkan pada salah satu ujungnya. Pada ujung-ujung yang lain diberi panas sengan suhu berbeda, 60º C dan 30º C. Jika panjang logam sama dan konduktifitas besi X dua kali lipat besi Y. Tentukan suhu pada sambungan kedua logam!

Lempengan tembaga yang dipanaskan salah satu ujungnya memiliki panjang 4 m dan lebarnya 2 m. suhu masing-masing ujung tembaga adalah 33º C dan 43º C. Konduksi termal tembaga adalah 8 × 10^-1 W/mK. Berapa jumlah kalor yang mengalir?

Contoh soal dinding Komposit. Sebatang tembaga murni dengan panjang 100 cm dipanaskan hingga mencapai temperatur 300^°C. Bila lebar tembaga 100 cm dan tebalnya 1 cm, tentukan panas yang berpindah bila temperatur sekelilingnya 50^Oc dengan koefisien perpan tembaga, k = 369 W/mK!

Rumus Fisika Lainnya

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Asteroid Ryugu mengandung setidaknya 15 asam amino

Fisika Partikel | Definisi, Contoh dan Penjelasan

Radiasi Nuklir | Dari mana asalnya?

Tinggalkan Balasan Batalkan balasan

Konduksi Panas dan Hukum Fourier – Rumus, Contoh Soal dan Jawaban

Konduksi Panas

Rumus Konduksi

Dinding yang berbentuk geometri sederhana

Silinder berlubang

Cangkang yang berbentuk bola dan paralepipeda

Pengaruh Konduktivitas termal yang tak seragam

Struktur komposit

Contoh Konduksi Panas

Hukum Fourier

Hukum Fourier dapat dinyatakan dalam 2 bentuk ekivalen:

Bentuk diferensial

Bentuk integral

Contoh Soal + Jawaban Konduksi Panas

Sebuah batang logam mempunyai panjang 2 m, dan memiliki luas penampang 20 cm2 dan perbedaan suhu kedua ujungnya 500C. Bila koefisien konduksi termalnya 0,2 kal/ms0C, tentukan jumlah kalor yang merambat per satuan luas & per satuan waktu!

Batang besi dengan panjang 4 m, memiliki luas penampang 24 cm2, dan perbedaan suhu kedua ujungnya 50º C. Jika koefisien konduksi termalnya 0,2 kal/msC. Tentukan jumlah kalor yang dirambatkan!

Faktor-faktor yang tidak memengaruhi laju perpindahan kalor secara konduksi pada sebuah logam adalah…

Suatu batang logam yang salah satu ujungnya dipanasi. Batang logam tersebut memiliki luas penampang 25 cm2 dan konduktifitas termal 4.105 J/smC. Panjang batang logam tersebut 8 m dan perbedaan suhu kedua ujungnya 30º C. Kalor yang merambat dalam batang besi selama 2 detik adalah…

Contoh soal silinder berlubang. Pipa dengan jari-jari 40 mm dan panjang 4 m yang diberi lapisan isolasi setebal 4 cm dengan koefisien perpan, k = 0,744 W/mK memiliki temperatur 20°C dan 30°C, tentukan laju aliran panas yang terjadi!

Lempengan tembaga mempunyai luas penampang 25 cm2 panjang 55 cm. Jika perubahan suhu kedua ujungnya 50º C dan konduktifitas kalor dari tembaga adalah 0,16 W/mK. Berapa laju perpindahan kalor?

Soal dinding datar. Dinding sebuah gudang memiliki temperatur 23°C pada bagian dalam dan 30°C pada bagian luar dengan koefisien perpan dinding, k = 2,69 W/mK serta tebal dinding 15 cm, tentukan laju aliran panas/ satuan luas yang terjadi !

Dua batang besi X dan Y disambungkan pada salah satu ujungnya. Pada ujung-ujung yang lain diberi panas sengan suhu berbeda, 60º C dan 30º C. Jika panjang logam sama dan konduktifitas besi X dua kali lipat besi Y. Tentukan suhu pada sambungan kedua logam!

Lempengan tembaga yang dipanaskan salah satu ujungnya memiliki panjang 4 m dan lebarnya 2 m. suhu masing-masing ujung tembaga adalah 33º C dan 43º C. Konduksi termal tembaga adalah 8 × 10-1 W/mK. Berapa jumlah kalor yang mengalir?

Contoh soal dinding Komposit. Sebatang tembaga murni dengan panjang 100 cm dipanaskan hingga mencapai temperatur 300°C. Bila lebar tembaga 100 cm dan tebalnya 1 cm, tentukan panas yang berpindah bila temperatur sekelilingnya 50Oc dengan koefisien perpan tembaga, k = 369 W/mK!

Rumus Fisika Lainnya

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Asteroid Ryugu mengandung setidaknya 15 asam amino

Fisika Partikel | Definisi, Contoh dan Penjelasan

Radiasi Nuklir | Dari mana asalnya?

Tinggalkan Balasan Batalkan balasan

Sebuah batang logam mempunyai panjang 2 m, dan memiliki luas penampang 20 cm²dan perbedaan suhu kedua ujungnya 50⁰C. Bila koefisien konduksi termalnya 0,2 kal/ms⁰C, tentukan jumlah kalor yang merambat per satuan luas & per satuan waktu!

Batang besi dengan panjang 4 m, memiliki luas penampang 24 cm², dan perbedaan suhu kedua ujungnya 50º C. Jika koefisien konduksi termalnya 0,2 kal/msC. Tentukan jumlah kalor yang dirambatkan!

Suatu batang logam yang salah satu ujungnya dipanasi. Batang logam tersebut memiliki luas penampang 25 cm²dan konduktifitas termal 4.10⁵ J/smC. Panjang batang logam tersebut 8 m dan perbedaan suhu kedua ujungnya 30º C. Kalor yang merambat dalam batang besi selama 2 detik adalah…

Contoh soal silinder berlubang. Pipa dengan jari-jari 40 mm dan panjang 4 m yang diberi lapisan isolasi setebal 4 cm dengan koefisien perpan, k = 0,744 W/mK memiliki temperatur 20^°C dan 30^°C, tentukan laju aliran panas yang terjadi!

Lempengan tembaga mempunyai luas penampang 25 cm² panjang 55 cm. Jika perubahan suhu kedua ujungnya 50º C dan konduktifitas kalor dari tembaga adalah 0,16 W/mK. Berapa laju perpindahan kalor?

Soal dinding datar. Dinding sebuah gudang memiliki temperatur 23^°C pada bagian dalam dan 30^°C pada bagian luar dengan koefisien perpan dinding, k = 2,69 W/mK serta tebal dinding 15 cm, tentukan laju aliran panas/ satuan luas yang terjadi !

Lempengan tembaga yang dipanaskan salah satu ujungnya memiliki panjang 4 m dan lebarnya 2 m. suhu masing-masing ujung tembaga adalah 33º C dan 43º C. Konduksi termal tembaga adalah 8 × 10^-1 W/mK. Berapa jumlah kalor yang mengalir?

Contoh soal dinding Komposit. Sebatang tembaga murni dengan panjang 100 cm dipanaskan hingga mencapai temperatur 300^°C. Bila lebar tembaga 100 cm dan tebalnya 1 cm, tentukan panas yang berpindah bila temperatur sekelilingnya 50^Oc dengan koefisien perpan tembaga, k = 369 W/mK!