PINTERpandai
Pinter Pandai

Kerangka Acuan Inersia dan non-inersia Bersama Contoh Soal dan Jawaban (Fisika)

5 min read

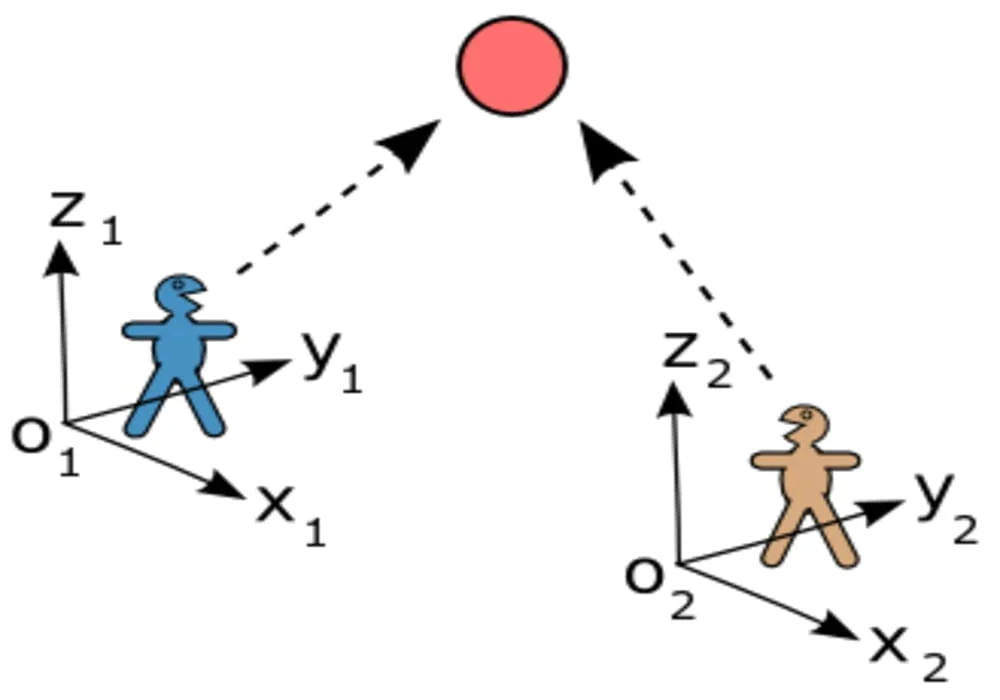
Kerangka acuan fisika

Kerangka Acuan

Kerangka acuan adalah suatu perspektif dari mana suatu sistem diamati. Dalam bidang fisika, suatu kerangka acuan memberikan suatu pusat koordinat relatif terhadap seorang pengamat yang dapat mengukur gerakan dan posisi semua titik yang terdapat dalam sistem, termasuk orientasi obyek di dalamnya.

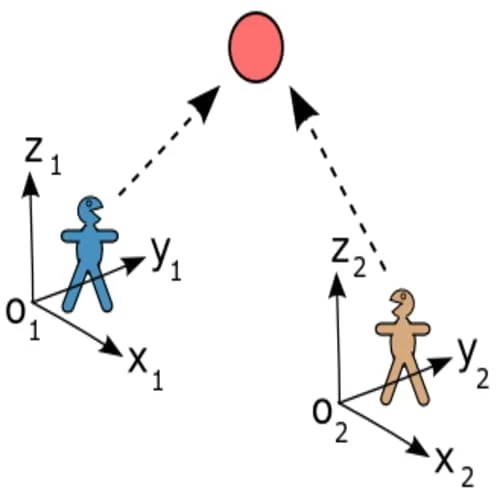
Kerangka acuan fisika
2 Buah kerangka acuan.

Jenis kerangka acuan

Terdapat dua jenis kerangka acuan, yaitu: kerangka acuan inersia dan non-inersia. Jenis yang pertama adalah jenis kerangka acuan yang telah diisyaratkan oleh prinsip relativitas Newtonian.

Kerangka acuan inersia

Suatu kerangka acuan inersia bertranslasi dengan suatu kecepatan konstan, yang berarti kerangka acuan itu tidak berotasi (hanya bertranslasi) dan pusat koordinatnya bergerak dengan kecepatan konstan di sepanjang sebuah garis lurus (dengan kecepatan tetap, tanpa adanya komponen percepatan). Dalam kerangka acuan inersia, berlaku hukum pertama Newton (inersia) dan juga hukum gerak Newton.

Beberapa cara untuk mendeskripsikan secara singkat suatu kerangka acuan inersial, antara lain adalah:

  • Bergerak dengan kecepatan konstan.
  • Yang tidak bergerak dipercepat.
  • Yang di mana hukum inersia berlaku.
  • Yang di mana hukum gerak Newton berlaku.
  • Yang di mana tidak terdapat gaya-gaya fiktif.

Kerangka acuan non-inersia

Suatu kerangka acuan non-inersia, sebagai contoh mobil yang bergerak melingkar, atau komidi putar yang sedang berputar, berakselerasi atau/dan berputar. Hukum pertama Newton tidak berlaku dalam kerangka acuan non-inersial, yang terlihat dengan adanya percepatan pada obyek tanpa adanya gaya yang menyebabkannya dalam kerangka acuan tersebut.

Kecepatan konstan saja tidak cukup untuk membuat suatu kerangka acuan menjadi kerangka acuan inersia, ia juga harus bergerak dalam garis lurus. Gerak berputar atau melengkung akan menyebabkan kerangka acuan tidak lagi menjadi inersia dikarenakan munculnya percepatan sentripetal.

Beberapa cara singkat untuk mendeskripsikan kerangka acuan non-inersia, misalnya:

  • Yang kecepatannya berubah (berubah dipercepat, diperlambat atau bergerak dalam lintasan tidak lurus, –berbelok-belok–).
  • Suatu kerangka acuan yang dipercepat.
  • Suatu kerangka acuan yang di mana hukum inersia tidak lagi berlaku.
  • Suatu kerangka acuan yang di mana muncul gaya-gaya fiktif agar hukum gerak Newton tetap berlaku.

Ilustrasi kerangka acuan inersia

Secara umum jika suatu kerangka acuan inersia telah dipilih, maka diharapkan bahwa pengamatan yang dilakukan langsung pada obyek pengamatan itu atau hanya dari kerangka acuan relatif yang dipilih akan memberikan hasil pengamatan yang sama. Jika tidak, berarti ada yang salah dalam proses pemilihan kerangka atau dikatakan bahwa kerangka acuan tidak inersial.

Kerangka acuan yang diam

Sebagai ilustrasi di bawah ini diambil kasus sebuah benda dijatuhkan tanpa kecepatan awal (gerak jatuh bebas) dari atas sebuah gedung. Dimisalkan terdapat kemungkinan tiga pilihan titik (di atas gedung, di tengah dan di bawah) dan dua arah (ke atas dan ke bawah) untuk menentukan kerangka acuan inersial. Di sini diambil kasus khusus, yaitu antara koordinat semesta dan koordinat pengamat tidak saling bergerak satu sama lain (kecepatan konstan = 0).

Catatan:

  • {\displaystyle y_{0}\!}: posisi awal.
  • {\displaystyle y_{a}\!}: posisi akhir.
  • {\displaystyle a\!}: percepatan.
  • {\displaystyle h\!}: posisi pengamat di atas, dihitung dari lantai gedung.
  • {\displaystyle h_{T}\!}: posisi pengamat di tengah, dihitung dari lantai gedung.
  • {\displaystyle t_{a}\!}: waktu akhir, waktu yang diperlukan benda untuk sampai ke lantai gedung.
  • {\displaystyle s_{a}\!}: jarak akhir, jarak yang diperlukan benda untuk sampai ke lantai gedung dihitung dari posisi mula-mula ia dilepaskan.

Kasus 1

GambarPosisi

pengamat

Arah y+Persamaan gerakJarak/waktu

tempuh

di atas

{\displaystyle y_{0}=0\!}

{\displaystyle y_{a}=-h\!}

ke atas

{\displaystyle a=-g\!}

{\displaystyle y(t)=y_{0}+{\frac {1}{2}}at^{2}\!}{\displaystyle t_{a}={\sqrt {\frac {2h}{g}}}\!}

{\displaystyle s_{a}=h\!}

Kasus 2

GambarPosisi

pengamat

Arah y+Persamaan gerakJarak/waktu

tempuh

di atas

{\displaystyle y_{0}=0\!}

{\displaystyle y_{0}=h\!}

ke bawah

{\displaystyle a=g\!}

{\displaystyle y(t)=y_{0}+{\frac {1}{2}}at^{2}\!}{\displaystyle t_{a}={\sqrt {\frac {2h}{g}}}\!}

{\displaystyle s_{a}=h\!}

Kasus 3

GambarPosisi

pengamat

Arah y+Persamaan gerakJarak/waktu

tempuh

di tengah

{\displaystyle y_{0}=(h-h_{T})\!}

{\displaystyle y_{a}=-h_{T}\!}

ke atas

{\displaystyle a=-g\!}

{\displaystyle y(t)=y_{0}+{\frac {1}{2}}at^{2}\!}{\displaystyle t_{a}={\sqrt {\frac {2h}{g}}}\!}

{\displaystyle s_{a}=h\!}

Kasus 4

GambarPosisi

pengamat

Arah y+Persamaan gerakJarak/waktu

tempuh

di tengah {\displaystyle y_{0}=-(h-h_{T})\!}

{\displaystyle y_{a}=h_{T}\!}

ke bawah

{\displaystyle a=g\!}

{\displaystyle y(t)=y_{0}+{\frac {1}{2}}at^{2}\!}{\displaystyle t_{a}={\sqrt {\frac {2h}{g}}}\!}

{\displaystyle s_{a}=h\!}

Kasus 5

GambarPosisi

pengamat

Arah y+Persamaan gerakJarak/waktu

tempuh

di bawah

{\displaystyle y_{0}=h\!}

{\displaystyle y_{a}=0\!}

ke atas

{\displaystyle a=-g\!}

{\displaystyle y(t)=y_{0}+{\frac {1}{2}}at^{2}\!}{\displaystyle t_{a}={\sqrt {\frac {2h}{g}}}\!}

{\displaystyle s_{a}=h\!}

Kasus 6

GambarPosisi

pengamat

Arah y+Persamaan gerakJarak/waktu

tempuh

di bawah

{\displaystyle y_{0}=-h\!}

{\displaystyle y_{a}=0\!}

ke bawah

{\displaystyle a=-g\!}

{\displaystyle y(t)=y_{0}+{\frac {1}{2}}at^{2}\!}{\displaystyle t_{a}={\sqrt {\frac {2h}{g}}}\!}

{\displaystyle s_{a}=h\!}

Nilai {\displaystyle t_{a}\!} dicari dengan menggunakan

{\displaystyle t_{a}={\sqrt {\frac {2(y_{a}-y_{0})}{a}}}}

dan {\displaystyle s_{a}\!}

{\displaystyle s_{a}=|y_{a}-y_{0}|\!}

Dalam contoh ini (kasus 1 – 6) telah dibuktikan bahwa nilai {\displaystyle t_{a}\!} dan {\displaystyle s_{a}\!} bernilai sama, tidak tergantung di mana pengamatan dilakukan dan arah y mana yang positif. Dan memang seharusnya demikian. Coba bayangkan apabila hukum-hukum yang sama tidak berlaku pada kerangka inersia, bagaimana orang dapat mengamati pergerakan awan, peredaran planet dan sebagainya dari bumi. Kita harus berada di sana untuk mengamatinya karena hasil yang didapat akan berbeda dengan pengamatan yang dilakukan dari bumi. Untunglah terdapat konsep ini sehingga pengamatan dapat dilakukan di tempat lain dan akan tetap memperoleh hasil yang sama.

Kerangka acuan yang bergerak lurus beraturan

Bus-Inertial.png

Ilustrasi dalam contoh ini adalah seorang pengamat {\displaystyle P_{1}\!} sedang berada di atas sebuah bus {\displaystyle B\!} yang bergerak lurus beraturan ({\displaystyle v=tetap\!}) terhadap pengamat lain {\displaystyle P_{1}\!}yang diam di suatu tempat. Sebuah obyek {\displaystyle O\!} di-jatuhbebas-kan di atas bis. Kedua pengamat harus mengukur jarak tempuh dan waktu tempuh yang sama (dari posisi awal dijatuhkan sampai mencapai atap bis) karena kedua pengamat dilihat dari yang lainnya berada pada kerangka acuan inersial.

Ilustrasi kerangka acuan non-inersial

Contoh sederhana kerangka acuan non-inersial adalah apabila suatu kerangka acuan bergerak lurus dipercepat atau bergerak melingkar (rotasi).

Pegas dalam lift

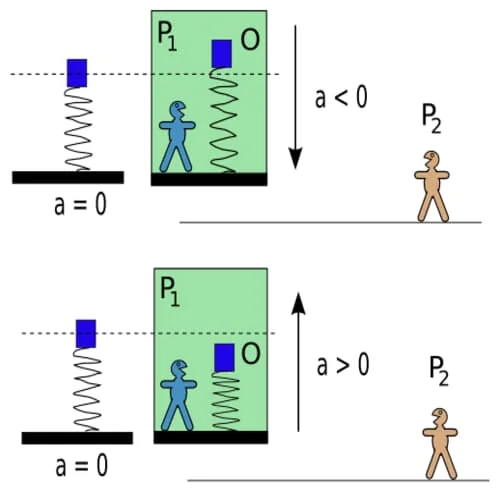
Pegas dalam lift kerangka acuan fisika

Suatu contoh sederhana kerangka acuan non-inersia adalah kerangka acuan yang diletakkan dalam suatu lift dipercepat (baik ke atas maupun ke bawah).

Suatu benda dan pegas diletakkan di dalam lift untuk membuktikan hal tersebut. Pengamat {\displaystyle P_{1}\!} adalah pengamat dalam lift yang tidak bergerak terhadap obyek {\displaystyle O\!} berupa suatu massa dan pegas, sedangkan pengamat {\displaystyle P_{2}\!} adalah pengamat yang diam terhadap tanah.

Bila lift merupakan suatu kerangka acuan inersial ({\displaystyle a=0\!}) maka panjang pegas adalah sama seperti panjang pegas mula-mula.

Akan tetapi bila lift dipercepat maka panjang pegas akan berubah. Pengamat {\displaystyle P_{1}\!} akan menyaksikan suatu gaya fiktif bekerja pada pegas yang menyebabkan panjangnya berubah, padahal tidak ada gaya yang dikenakan padanya. Lain halnya dengan pengamat {\displaystyle P_{2}\!} yang dengan jelas melihat mengapa pegas dapat berubah panjangnya. Hal ini dikarenakan lift yang bergerak dipercepat memberikan gaya normal kepada pegas sehingga panjangnya berubah.

Gerak melingkar

Circular motion.png

Gerak melingkar merupakan contoh sederhana lain dari suatu tempat di mana peletakan suatu kerangka acuan padanya akan menyebabkan kerangka acuan menjadi non-inersia, walapun gerak melingkar yang dimaksud memiliki kecepatan putar tetap (gerak melingkar beraturan). Kecepatan putaran tetap adalah kecepatan linier yang diubah selalu arahnya setiap saat (dipercepat) dengan teratur, jadi pada dasarnya adalah suatu gerak berubah beraturan.

Dalam gerak melingkar baik yang vertikal, horisontal maupun di antaranya, terdapat perbedaan pengamatan antara pengamat yang diam di atas tanah {\displaystyle P_{2}\!} dengan pengamat yang bergerak bersama obyek {\displaystyle O\!} yang diamati {\displaystyle P_{1}\!}, Pengamat {\displaystyle P_{1}\!} dengan jelas melihat adanya gaya tarik menuju pusat yang selalu merubah arah gerak obyek sehingga bergerak melingkar (tanpa adanya gaya ini obyek akan terlempar keluar, hukum inersia Newton), akan tetapi {\displaystyle P_{2}\!} tidak menyadari hal ini. {\displaystyle P_{2}\!} tidak mengerti mengapa ia tidak jatuh (meluncur) padahal ia membuat sudut {\displaystyle A\!} dengan arah vertikal. Dalam kasus ini timbul gaya fiktif yang seakan-akan menahan pengamat {\displaystyle P_{2}\!} sehingga tidak jatuh.

Contoh Soal Kerangka Acuan

Tentukan mana yang merupakan kerangka acuan inersial dan mana yang bukan:

  • pesawat terbang yang jatuh akibat kerusakan mesin, semakin lama semakin cepat.

  • orang terjun payung yang jatuh dengan kecepatan konstan akibat adanya gesekan udara.

Jawaban:

Obyek yang dapat digunakan sebagai kerangka acuan inersial haruslah bergerak lurus dengan kecepatan tetap. Dari kedua contoh tersebut hanyalah orang terjun payung yang memenuhi. Hambatan udara yang proporsional dengan kecepatan, akan menciptakan kecepatan terminal pada akhirnya. Artinya pada kecepatan terminal ini, penerjun payung baru boleh digunakan sebagai kerangka acuan inersial dan tidak sebelumnya.

Sebuah bus bergerak ke kanan dengan kecepatan tetap 5 m/s. Di atasnya berdiri seorang anak yang sedang melempar bola secara vertikal ke atas dengan kecepatan awal 10 m/s. Tentukan berapa waktu yang diperlukan bola untuk kembali ke tangan anak tersebut, apabila diamati oleh:

  • anak itu sendiri, dan

  • orang yang lain yang diam di luar bis pada jarak 20 m saat bis belum bisa bergerak.

Jawaban:

Dikarenakan bus bergerak dengan kecepatan tetap, maka baik si anak atau orang lain yang mengamati, keduanya masing-masing merupakan kerangka acuan inersial, dengan demikian hasil yang diperoleh adalah sama, yaitu: 2 s.

Permasalah ini melibatkan persamaan:

{\displaystyle h(t)=v_{0}t-{\frac {1}{2}}gt^{2}}

di mana ingin dicari saat {\displaystyle \!h(t)=0} yang akan dipenuhi hanya oleh {\displaystyle \!t=0\ s} dan {\displaystyle \!t=2\ s}. Jawaban kedua yang dipilih, karena jawaban yang pertama adalah saat mula-mula bola dilemparkan.

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber foto: Isaac Physics, Study

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

Pinter Pandai
«
»

Rahasia Kehidupan Harimau: Mengenal Lebih Dekat dengan Sang Raja…

PinterPandai
Mar 24, 2024 3 min read

Asteroid Apophis “Dewa Kekacauan” dan Bumi: data baru pada…

PinterPandai
Mar 10, 2024 2 min read

Keajaiban Bintang Jatuh (Shooting Stars): Gemerlap Meteor di Langit…

PinterPandai
Jan 17, 2024 1 min read

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *