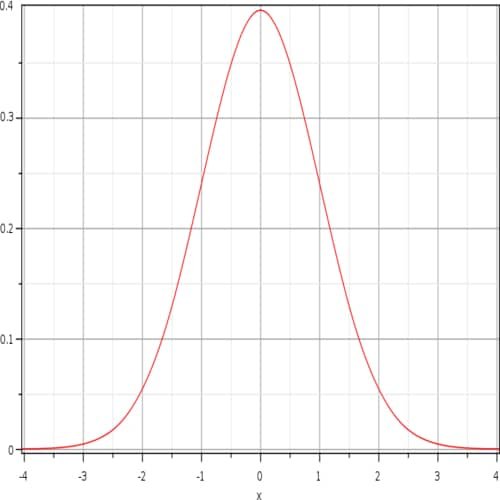
Hukum Gauss (medan listrik) | Integral, Fungsi, Rumus, Soal dan Jawaban

Dalam ilmu matematika, fungsi Gauss adalah fungsi yang berbentuk sebagai berikut:

f(x)=ae^{-{\frac {(x-b)^{2}}{2c^{2}}}}

$a$ , $b$ dan $c$ adalah konstanta riil.

Fungsi ini dinamai dari matematikawan Jerman Carl Friedrich Gauss. Fungsi Gauss seringkali digunakan untuk mewakili fungsi kepekatan probabilitas variabel acak yang didistribusi secara normal dengan nilai harapan $μ = b$ dan variansi $σ 2 = c 2$ .

Fungsi kepekatan probabilitas variabel acak

Dalam kasus ini, bentuk fungsi Gaussnya adalah:

g(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}.

Grafik fungsi Gauss adalah kurva yang berbentuk “lonceng” dan simetris. Parameter $a$ adalah tinggi puncak kurva, $b$ adalah posisi di tengah puncak dan $c$ (deviasi standar / simpangan baku) mengendalikan “lebar” lonceng.

Fungsi Gauss sering digunakan dalam ilmu statistika untuk mendeskripsikan distribusi normal, dalam pemrosesan sinyal untuk mendefinisikan filter Gaus, dalam pemrosesan gambar yang menggunakan fungsi Gauss dua dimensi untuk membuat kekaburan Gauss, dan dalam ilmu matematika untuk menyelesaikan persamaan panas dan persamaan difusi dan untuk mendefinisikan transformasi Weierstrass.

Integral Gauss

Grafik f(x) = e^−x2 dan luas di antara fungsi tersebut dan sumbu x, yang sama dengan $\scriptstyle {\sqrt {\pi }}$ .

Integral Gauss, juga dikenal dengan nama integral Euler–Poisson, adalah integral fungsi Gauss e^−x2 di sepanjang garis riil. Konsep ini dinamai dari matematikawan Jerman Carl Friedrich Gauss. Integral ini adalah:

\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}

Integral ini dapat diaplikasikan untuk berbagai macam hal. Contohnya, dengan sedikit perubahan dalam variabel, integral ini digunakan untuk menghitung konstanta normalisasi distribusi normal. Integral yang sama dengan limit yang terbatas sangat terkait dengan fungsi error dan fungsi distribusi kumulatif distribusi normal. Integral ini juga sering digunakan dalam ilmu fisika (khususnya mekanika kuantum).

Penghitungan integral Gauss

Koordinat polar integral gauss

Cara standar untuk menghitung integral Gauss adalah dengan menggunakan koordinat polar.

$\left(\int _{-\infty }^{\infty }e^{-x^{2}}\,dx\right)^{2}=\int _{-\infty }^{\infty }e^{-x^{2}}\,dx\int _{-\infty }^{\infty }e^{-y^{2}}\,dy=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-(x^{2}+y^{2})}\,dx\,dy$

Pertimbangkan fungsi e^{−(x2 + y2)} = e^−r2 di bidang R², dan hitung integral dengan dua cara:
1. di satu sisi, dengan integral lipat dalam sistem koordinat Kartesius, integralnya dilipatkan dua:
  $\left(\int e^{-x^{2}}\,dx\right)^{2};$
2. di sisi lain, apabila menggunakan integral kulit tabung (integrasi lipat dalam sistem koordinat polar), hasilnya adalah π.

Berikut adalah penyelesaian yang menunjukkan bahwa hasilnya adalah pi:

${\begin{aligned}\iint _{\mathbf {R} ^{2}}e^{-(x^{2}+y^{2})}\,d(x,y)&=\int _{0}^{2\pi }\int _{0}^{\infty }e^{-r^{2}}r\,dr\,d\theta \\&=2\pi \int _{0}^{\infty }re^{-r^{2}}\,dr\\&=2\pi \int _{-\infty }^{0}{\tfrac {1}{2}}e^{s}\,ds&&s=-r^{2}\\&=\pi \int _{-\infty }^{0}e^{s}\,ds\\&=\pi (e^{0}-e^{-\infty })\\&=\pi ,\end{aligned}}$

Hukum Gauss

Pada ilmu fisika, Hukum Gauss atau Teorema fluks Gauss adalah hukum yang menghubungkan distribusi muatan listrik dengan medan listrik yang dihasilkannya.

Hukum ini dirumuskan oleh Carl Friedrich Gauss tahun 1835, tetapi tidak dipublikasikan sampai 1867. Merupakan salah satu dari empat persamaan Maxwell, yang menjadi basis bagi elektrodinamika klasik, tiga lainnya adalah Hukum Gauss tentang magnetisme, Hukum induksi Faraday, dan Hukum rangkaian Ampère. Hukum Gauss dapat digunakan untuk menurunkan Hukum Coulomb.

Contoh Soal dan Jawaban Hukum Gauss

1. Jika pusat sebuah bola berjari-jari 1 m terdapat muatan sebesar +2 μC, besar fluks listrik yang keluar dari permukaan bola mendekati…

A.0,65 x 10⁵Nm²/C
B. 1,13 x 10⁵Nm²/C
C. 2,26 x 10⁵Nm²/C
D. 4,48 x 10⁵Nm²/C
E. 8,99 x 10⁵Nm²/C

Jawaban:
Fluks listrik yang keluar dari permukaan bola dapat dicari dengan menggunakan
Φ = ∮E•n dS = q/ε₀ = +2 x 10^-6 C/(8,85 x 10^-12)
Φ = 2,26 x 10⁵ Wb.

2. Cindy memiliki sebuah bidang lingkaran dengan jari-jari 7 cm. Jika ada kuat medan listrik sebesar 200 N/C mengarah pada bidang tersebut dengan membentuk sudut 30⁰ terhadap bidang. Tentukan berapa fluks listrik tersebut?

Jawaban:
Luas Bidang = Luas lingkaran = π r² = 22/7 x 49 = 154 cm² = 1,54 x 10-2 m²
Cos θ = Cos 60^o
( θ = sudut yang dibentuk oleh E dan garis normal — lihat gambar sebelumnya –)
Φ = E. A.cos θ
Φ = 200. 1,54 x 10^-2 . 0,5
Φ = 1,54 weber.

3. Sebuah bola berjari-jari 0,5 meter dan di pusat bola terdapat muatan listrik 10 μC. Tentukan fluks listrik yang melalui bola!

Pembahasan

Diketahui:

Jari-jari bola (r) = 0,5 meter
Muatan listrik (Q) = 10 μC = 10 x 10^-6 C

Ditanya : Fluks listrik (Φ)

Jawab :

Medan listrik :

E = k q/r²
E = (9 x 10⁹ Nm²/C²)(10 x 10^-6 C) / 0,5²
E = (90 x 10³) / 0,25
E = 360 x 10³
E = 3,60 x 10⁵ N/C

Luas permukaan bola:

A = 4 π r² = 4 (3,14)(0,5)² = (12,56)(0,25) = 3,14 m²

Fluks listrik:

Garis medan listrik tegak lurus dengan permukaan dan berhimpit dengan garis normal sehingga sudut yang terbentuk 0^o.

Φ = E A cos θ
Φ = (3,60 x 10⁵)(3,14)(cos 0)
Φ = (11,304 x 10⁵)(1)
Φ = 11,304 x 10⁵
Φ = 1,13 x 10⁶ Nm²/C

4. Jika terdapat persegi dengan panjang sisi 20 cm, lalu bila sebuah medan listrik homogen sebesar 200 N/C ditembakkan ke arahnya dengan arah yang tegak lurus bidang persegi tersebut, berapa jumlah garis medan listrik yang menembus bidang persegi tersebut (fluks listrik)?

Jawaban:
Luas Persegi = 20 x 20 = 400 cm² = 4 x 10^-2 m²
Jumlah Garis yang menembus bidang
Φ = E. A
Φ = 200. 4 x 10^-2 m
Φ = 8 weber

5. Medan listrik sebesar 5000 N/C melewati permukaan persegi dan membentuk sudut 60^o terhadap garis normal. Luas permukaan persegi adalah 2 m². Tentukan fluks listrik yang melalui permukaan persegi!

Pembahasan:

Diketahui:

Medan listrik (E) = 5000 N/C
Luas permukaan (A) = 2 m²

θ = 60^o

Ditanya :

Fluks listrik (Φ)

Jawaban:

Fluks listrik :

Φ = E A cos θ
= (5000)(2)(cos 60)
= (5000)(2)(0,5)
= 5000 = 5 x 10³ Nm²/C

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Physics Classroom, Tutor Vista

Hukum Gauss (medan listrik) | Integral, Fungsi, Rumus, Soal dan Jawaban

Bunyi Hukum Gauss

Konversi satuan Gauss

Bentuk integral Hukum Gauss

Rumus Hukum Gauss

Fluks listrik Φ_E didefinisikan sebagai integral permukaan medan listrik:

Fungsi Gauss

Dalam ilmu matematika, fungsi Gauss adalah fungsi yang berbentuk sebagai berikut:

Fungsi kepekatan probabilitas variabel acak

Integral Gauss

Penghitungan integral Gauss

Koordinat polar integral gauss

Berikut adalah penyelesaian yang menunjukkan bahwa hasilnya adalah pi:

Hukum Gauss

Contoh Soal dan Jawaban Hukum Gauss

1. Jika pusat sebuah bola berjari-jari 1 m terdapat muatan sebesar +2 μC, besar fluks listrik yang keluar dari permukaan bola mendekati…

2. Cindy memiliki sebuah bidang lingkaran dengan jari-jari 7 cm. Jika ada kuat medan listrik sebesar 200 N/C mengarah pada bidang tersebut dengan membentuk sudut 30⁰ terhadap bidang. Tentukan berapa fluks listrik tersebut?

3. Sebuah bola berjari-jari 0,5 meter dan di pusat bola terdapat muatan listrik 10 μC. Tentukan fluks listrik yang melalui bola!

4. Jika terdapat persegi dengan panjang sisi 20 cm, lalu bila sebuah medan listrik homogen sebesar 200 N/C ditembakkan ke arahnya dengan arah yang tegak lurus bidang persegi tersebut, berapa jumlah garis medan listrik yang menembus bidang persegi tersebut (fluks listrik)?

5. Medan listrik sebesar 5000 N/C melewati permukaan persegi dan membentuk sudut 60^o terhadap garis normal. Luas permukaan persegi adalah 2 m². Tentukan fluks listrik yang melalui permukaan persegi!

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Asteroid Ryugu mengandung setidaknya 15 asam amino

Fisika Partikel | Definisi, Contoh dan Penjelasan

Radiasi Nuklir | Dari mana asalnya?

Tinggalkan Balasan Batalkan balasan

Hukum Gauss (medan listrik) | Integral, Fungsi, Rumus, Soal dan Jawaban

Bunyi Hukum Gauss

Konversi satuan Gauss

Bentuk integral Hukum Gauss

Rumus Hukum Gauss

Fluks listrik ΦE didefinisikan sebagai integral permukaan medan listrik:

Fungsi Gauss

Dalam ilmu matematika, fungsi Gauss adalah fungsi yang berbentuk sebagai berikut:

Fungsi kepekatan probabilitas variabel acak

Integral Gauss

Penghitungan integral Gauss

Koordinat polar integral gauss

Berikut adalah penyelesaian yang menunjukkan bahwa hasilnya adalah pi:

Hukum Gauss

Contoh Soal dan Jawaban Hukum Gauss

1. Jika pusat sebuah bola berjari-jari 1 m terdapat muatan sebesar +2 μC, besar fluks listrik yang keluar dari permukaan bola mendekati…

2. Cindy memiliki sebuah bidang lingkaran dengan jari-jari 7 cm. Jika ada kuat medan listrik sebesar 200 N/C mengarah pada bidang tersebut dengan membentuk sudut 300 terhadap bidang. Tentukan berapa fluks listrik tersebut?

3. Sebuah bola berjari-jari 0,5 meter dan di pusat bola terdapat muatan listrik 10 μC. Tentukan fluks listrik yang melalui bola!

4. Jika terdapat persegi dengan panjang sisi 20 cm, lalu bila sebuah medan listrik homogen sebesar 200 N/C ditembakkan ke arahnya dengan arah yang tegak lurus bidang persegi tersebut, berapa jumlah garis medan listrik yang menembus bidang persegi tersebut (fluks listrik)?

5. Medan listrik sebesar 5000 N/C melewati permukaan persegi dan membentuk sudut 60o terhadap garis normal. Luas permukaan persegi adalah 2 m2. Tentukan fluks listrik yang melalui permukaan persegi!

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Asteroid Ryugu mengandung setidaknya 15 asam amino

Fisika Partikel | Definisi, Contoh dan Penjelasan

Radiasi Nuklir | Dari mana asalnya?

Tinggalkan Balasan Batalkan balasan

Fluks listrik Φ_E didefinisikan sebagai integral permukaan medan listrik:

2. Cindy memiliki sebuah bidang lingkaran dengan jari-jari 7 cm. Jika ada kuat medan listrik sebesar 200 N/C mengarah pada bidang tersebut dengan membentuk sudut 30⁰ terhadap bidang. Tentukan berapa fluks listrik tersebut?

5. Medan listrik sebesar 5000 N/C melewati permukaan persegi dan membentuk sudut 60^o terhadap garis normal. Luas permukaan persegi adalah 2 m². Tentukan fluks listrik yang melalui permukaan persegi!