Hiperbola

Hiperbola adalah salah satu dari tiga jenis irisan kerucut, yang dibentuk oleh irisan suatu bidang dan kerucut ganda.

Persamaan hiperbola dengan pusat O (0, 0).

Vertikal: (x²/b²) – (y²/a²) = 1

Horisontal: (x²/a²) – (y²/b²) = 1

keterangan:

a : ½ x Panjang sumbu nyata
b : ½ x panjang sumbu imajiner

Rumus Hiperbola Vertikal dan Horisontal pada Titik pusat (0,0)

	Vertikal	Horisontal
	Titik pusat (0,0)
Persamaan	${\frac {x^{2}}{b^{2}}}-{\frac {y^{2}}{a^{2}}}=1$	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$
Panjang sumbu mayor	$2a$	$2a$
Panjang sumbu minor	$2b$	$2b$
Panjang Latus Rectum	$L={\frac {2b^{2}}{a}}$	$L={\frac {2b^{2}}{a}}$
Fokus	$F(0,\pm c)$	$F(\pm c,0)$
Puncak	$P(0,\pm a)$	$P(\pm a,0)$
Asimtot	$y=\pm {\frac {a}{b}}x$	$y=\pm {\frac {b}{a}}x$
Eksentrisitas	$e={\frac {c}{a}}$	$e={\frac {c}{a}}$
	Titik pusat (h,k)
Persamaan	${\frac {(x-h)^{2}}{b^{2}}}-{\frac {(y-k)^{2}}{a^{2}}}=1$	${\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1$
Panjang sumbu mayor	$2a$	$2a$
Panjang sumbu minor	$2b$	$2b$
Panjang Latus Rectum	$L={\frac {2b^{2}}{a}}$	$L={\frac {2b^{2}}{a}}$
Fokus	$F(h,k\pm c)$	$F(h\pm c,k)$
Puncak	$P(h,k\pm a)$	$P(h\pm a,k)$
Asimtot	$(y-k)=\pm {\frac {a}{b}}(x-h)$	$(y-k)=\pm {\frac {b}{a}}(x-h)$
Eksentrisitas	$e={\frac {c}{a}}$	$e={\frac {c}{a}}$

dimana $c={\sqrt {a^{2}+b^{2}}}$

Rumus hiperbola soal — Tiga kerucut cahaya dengan lebar dan intensitas berbeda, dihasilkan oleh lampu halogen yang menunjuk ke bawah. Menggambar tiga kurva hiperbolik pada dinding vertikal di dekatnya. Ilustrasi dan sumber foto: Wikimedia Commons

Hiperbola muncul dalam berbagai hal:

sebagai kurva yang mewakili fungsi $f(x)=1/x$ pada bidang Sistem koordinat Kartesius,
sebagai garis edar yang diikuti oleh ujung bayangan jam matahari,
sebagai bentuk orbit terbuka (berbeda dengan orbit elips tertutup), seperti orbit pesawat ruang angkasa selama ada bantuan gravitasi melalui perputaran sebuah planet atau lebih umumnya setiap pesawat ruang angkasa yang melebihi kecepatan lepas dari planet terdekat,
sebagai jalur penampakan tunggal komet (yang melintas terlalu cepat untuk kembali ke tata surya),
sebagai lintasan hamburan dari partikel subatom (ditindaklanjuti dengan gaya tolak bukan gaya tarik tetapi prinsipnya sama),
dalam navigasi radio, ketika perbedaan antara jarak ke dua titik, tetapi bukan jarak itu sendiri, dapat ditentukan, dan seterusnya.

Contoh Soal dan Jawaban Hiperbola

1. Tentukan kedua titik fokus dari hiperbola: (x²/16) – (y²/9) = 1

Jawaban:

(x²/a²) – (y²/b²) = 1, jika kita melihat persamaan umumnya, maka kita peroleh a=4 dan b=3. Tentu c kita cari dengan rumus c²=a²+b², dan kita dapatkan c=5.

Sehingga koordinat titik fokus dari hiperbola tersebut adalah pm (5,0)

2. Buatlah gambar grafik dari persamaan: (x²/16) + (y²/9) = 1

Jawaban:

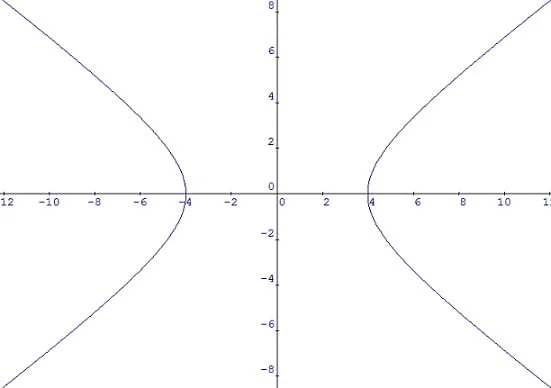
Soal grafik hiperbola — Grafik hiperbola (x²/16) + (y²/9) = 1

3. Tentukan titik pusat, titik focus, dan titik puncak hiperbola dengan persamaan y² – 2x² = 8.

Jawaban:

Persamaan hiperbola y² – 2x² = 8 diubah menjadi y²/8 – x²/4 = 1.

a² = 8 à a = 2√2
b² = 4 à b = 2
c² = a² + b² à c = √(8 + 4) = √12 = 2√3

Titik pusatnya yaitu pada O (0, 0).
Titik fokusnya yaitu (0, -c) = (0, -2√3) dan (0, c) = (0, 2√3).
Titik puncaknya yaitu (0, -a) = (0, -2√2) dan (0, a) = (0, 2√2).

4. Tentukan garis asimtot dari hiperbola: (x²/16) – y²/9) = 1

Jawaban:

(x²/a²) – (y²/b²) = 1, jika kita melihat persamaan umumnya, maka kita peroleh a=4 dan b=3. Kedua asimtotnya kita kenal sebagai $y= \pm \frac{b}{a}x$ , maka kita peroleh kedua asimtotnya adalah $y= \pm \frac{3}{4}x$

5. Soal untuk hiperbola vertikal. Tentukan kedua titik puncak, titik fokus dan garis asimtot untuk hiperbola : $\frac{y^2}{16}- \frac{x^2}{9}=1$ atau bisa juga dituliskan : $- \frac{x^2}{9}+ \frac{y^2}{16}=1$

Jawab :

Ketika kita mengambil y=0, kita tidak mungkin bisa menemukan nilai x. karena bentuk $- \frac{x^2}{9}=1$ adalah tidak akan terpenuhi untuk x berapapun.

Kita ambil x=0, maka kita dapatkan y=4. Inilah puncaknya. (gambar saja coret-coretan di x=4 dan x=-4 sebagai puncak, kemudian gambar hiperbola sederhana)

Perhatikan persamaan umum yang kita gunakan : $\frac{x^2}{a^2}- \frac{y^2}{b^2}=1$

(a itu miliknya x, berada di bawah (sebagai penyebut) dari x dan b itu miliknya y, berada di bawah (sebagai penyebut) dari y)

Sehingga, untuk soal : $- \frac{x^2}{9}+ \frac{y^2}{16}=1$

Kita dapatkan a=3 dan b=4

Sehingga garis asimtotnya pun adalah $y= \pm \frac{4}{3}x$

Untuk mencari titik fokus, kita perlu mencari c, yaitu kita dapatkan c itu sama dengan 5. Karena hiperbola vertikal, maka koordinat titik c adalah $(0, \pm c)$ yaitu sama dengan $(0, \pm 5)$ .

6. Diketahui Hiperbola dengan persamaan: 25x² – 144y² – 300x – 288y – 2844 = 0

Tentukan

Koordinat pusat
Jarak pusat ke puncak
Jarak antar puncak
Jarak pusat ke fokus
Jarak antar fokus
Koordinat puncak
Koordinat fokus
Panjang latus rectum
Eksentrisitas
Persamaan asimtot
Persamaan direktris

Jawaban:

25x² – 144y² – 300x – 288y – 2844 = 0
25x² – 300x – 144y² – 288y = 2844
25(x² – 12x) – 144(y² + 2y) = 2844
25[(x – 6)² – 36] – 144[(y + 1)² – 1] = 2844
25(x – 6)² – 900 – 144(y + 1)² + 144 = 2844
25(x – 6)² – 144(y + 1)² = 2844 – 144 + 900
25(x – 6)² – 144(y + 1)² = 3600

Jika kedua ruas dibagi dengan 3600 maka:

{(x-6)²/144) – (y+1)²/25)} =1

Jenis hiperbola adalah horizontal

a² = 144 maka a = 12
b² = 25 maka b = 5
c² = a² + b² = 144 + 25 = 169 maka c = 13

Koordinat pusat (6, – 1)

Jarak antar puncak = 2a = 24

Jarak pusat ke fokus = c = 13

Jarak antar fokus = 2c = 26

Koordinat puncak (12, 0)dan ( – 12 , 0)

Untuk memudahkan cara mencari puncak adalah sebagai berikut:

Menentukan Puncak Hiperbola

Untuk mendapatkan puncak maka absis pusat x = 6 kita tambah dengan a=12 atau kita kurangi dengan 12
Puncak kanan diperoleh dengan menambah absis dengan 12. x = 6 + 12 = 18, jadi puncaknya (18, –1)
Puncak kiri diperoleh dengan mengurangi absis dengan 12. x = 6 – 12 = –6 , jadi puncaknya (–6, –1)

Koordinat fokus (13, 0) dan ( – 13 , 0)

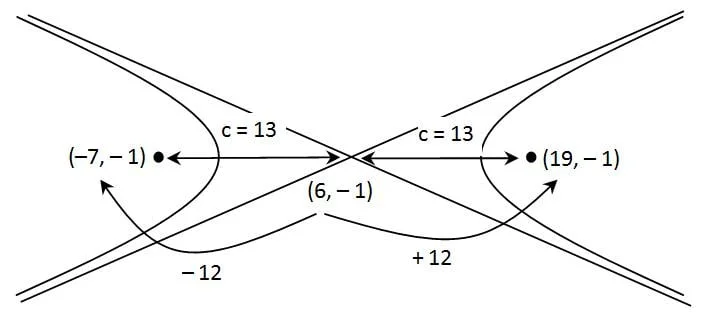
Untuk mendapatkan fokus maka absis pusat x = 6 kita tambah dengan c=13 atau kita kurangi dengan 13
Fokus kanan diperoleh dengan menambah absis dengan 13. x = 6 + 13 = 19, jadi fokusnya (19, –1)
Fokus kiri diperoleh dengan mengurangi absis dengan 13. x = 6 – 13 = –7 , jadi fokusnya (–7, –1)

Panjang latus rectum

2b²/a = 50/12 = 15/6

Eksentrisitas

e = c/a = 13/12

Persamaan asimtot

Persamaan asimtot untuk hiperbola horizontal dengan pusat (p, q) adalah:

y-q = ± b/a (x-p)
y+1 = ± 5/12 (x-6)
12y+12 = ±5(x-6)
12y+12 = ±(5x-30)
12y + 12 = 5x – 30 atau 12y + 12 = –5x + 30
5x – 12y – 42 = 0 atau 5x + 12y – 18 = 0

Jika tidak hafal dengan rumus maka cara mencari asimtot adalah dengan mengubah bilangan 1 di ruas kanan menjadi 0

Persamaan hiperbola

{(x-6)²/144) – (y+1)²/25} = 1
{(x-6)²/144) – (y+1)²/25} = 0
{(x-6)²/144) = (y+1)²/25}
25(x-6)² = 144(y+1)²
5(x-6) = ± 12(y+1)
5(x – 6) = 12(y + 1) atau 5(x – 6) = –12(y + 1)
5x – 30 = 12y + 12 atau 5x – 30 = –12y – 12
5x – 12y – 42 = 0 atau 5x + 12y – 18 = 0

Persamaan direktris

Jarak pusat ke direktris adalah

a/e = (12 / 13/12) = 144/13 = 11 1/13

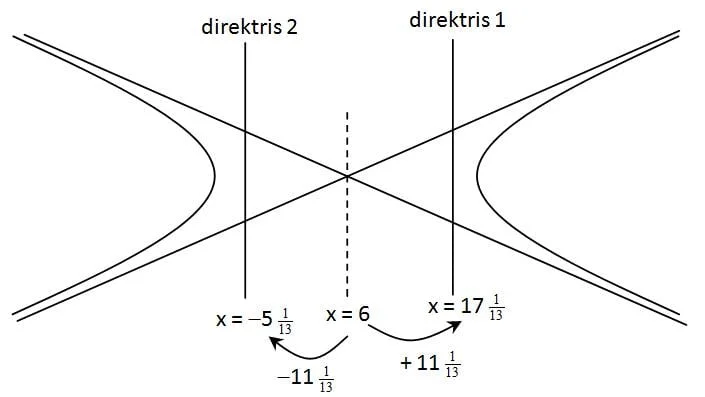
Untuk mendapatkan direktris maka absis yang ada di pusat (x = 6) kita tambah dengan 11 atau dikurangi 11

Direktris kanan x = 6 + 11 = 17

Direktris kiri x = 6 – 11 = –5

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math is Fun, Math Warehouse, Lumen Learning, Toppr

Hiperbola – Rumus, Persamaan, Contoh Soal dan Jawaban

Hiperbola

Persamaan hiperbola dengan pusat O (0, 0).

Rumus Hiperbola Vertikal dan Horisontal pada Titik pusat (0,0)

Hiperbola muncul dalam berbagai hal:

Contoh Soal dan Jawaban Hiperbola

1. Tentukan kedua titik fokus dari hiperbola: (x²/16) – (y²/9) = 1

2. Buatlah gambar grafik dari persamaan: (x²/16) + (y²/9) = 1

3. Tentukan titik pusat, titik focus, dan titik puncak hiperbola dengan persamaan y² – 2x² = 8.

4. Tentukan garis asimtot dari hiperbola: (x²/16) – y²/9) = 1

5. Soal untuk hiperbola vertikal. Tentukan kedua titik puncak, titik fokus dan garis asimtot untuk hiperbola : $\frac{y^2}{16}- \frac{x^2}{9}=1$ atau bisa juga dituliskan : $- \frac{x^2}{9}+ \frac{y^2}{16}=1$

6. Diketahui Hiperbola dengan persamaan: 25x² – 144y² – 300x – 288y – 2844 = 0

Tentukan

Koordinat pusat

Jarak pusat ke puncak

Jarak antar puncak

Jarak pusat ke fokus

Jarak antar fokus

Koordinat puncak

Koordinat fokus

Panjang latus rectum

Eksentrisitas

Persamaan asimtot

Persamaan direktris

Koordinat puncak (12, 0)dan ( – 12 , 0)

Koordinat fokus (13, 0) dan ( – 13 , 0)

Panjang latus rectum

Eksentrisitas

Persamaan asimtot

Persamaan hiperbola

Persamaan direktris

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

Hiperbola – Rumus, Persamaan, Contoh Soal dan Jawaban

Hiperbola

Persamaan hiperbola dengan pusat O (0, 0).

Rumus Hiperbola Vertikal dan Horisontal pada Titik pusat (0,0)

Hiperbola muncul dalam berbagai hal:

Contoh Soal dan Jawaban Hiperbola

1. Tentukan kedua titik fokus dari hiperbola: (x²/16) – (y²/9) = 1

2. Buatlah gambar grafik dari persamaan: (x²/16) + (y²/9) = 1

3. Tentukan titik pusat, titik focus, dan titik puncak hiperbola dengan persamaan y2 – 2x2 = 8.

4. Tentukan garis asimtot dari hiperbola: (x²/16) – y²/9) = 1

6. Diketahui Hiperbola dengan persamaan: 25x2 – 144y2 – 300x – 288y – 2844 = 0

Tentukan

Koordinat pusat

Jarak pusat ke puncak

Jarak antar puncak

Jarak pusat ke fokus

Jarak antar fokus

Koordinat puncak

Koordinat fokus

Panjang latus rectum

Eksentrisitas

Persamaan asimtot

Persamaan direktris

Koordinat puncak (12, 0)dan ( – 12 , 0)

Koordinat fokus (13, 0) dan ( – 13 , 0)

Panjang latus rectum

Eksentrisitas

Persamaan asimtot

Persamaan hiperbola

Persamaan direktris

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

3. Tentukan titik pusat, titik focus, dan titik puncak hiperbola dengan persamaan y² – 2x² = 8.

6. Diketahui Hiperbola dengan persamaan: 25x² – 144y² – 300x – 288y – 2844 = 0