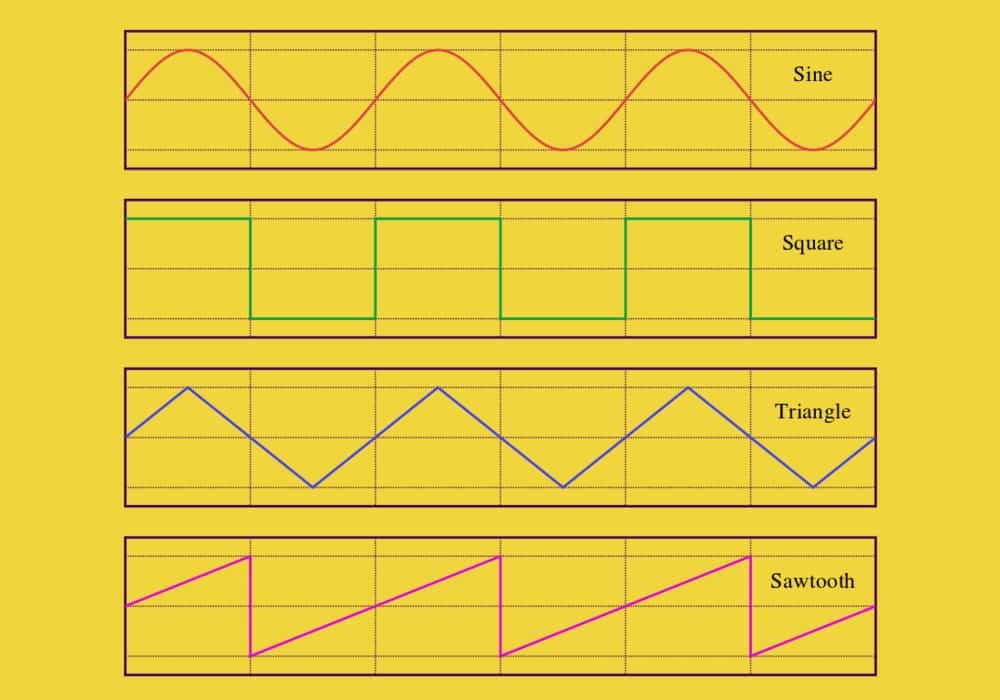
Penjelasan Gelombang Sinus
Gelombang sinus atau sinusoidal adalah fungsi matematika yang berbentuk osilasi halus berulang. Fungsi ini sering muncul dalam ilmu matematika, fisika, pengolahan sinyal, dan teknik listrik, dan berbagai bidang lain.
Bentuk paling sederhana dari fungsi gelomban sinus terhadap waktu )t) adalah
di mana:
- A, amplitudo, adalah puncak simpangan fungsi dari posisi tengahnya,
- ω, frekuensi sudut, menunjukkan berapa banyak gerak bolak-balik yang terjadi dalam satu satuan waktu, dalam radian per detik,
- φ, fase, menunjukkan di mana posisi awal gerakan ketika t=0,
- Jika fase tidak bernilai nol, seluruh gelombang akan tampak bergeser menurut sumbu X (sumbu waktu) sebesar φ/ω detik. Nilai negatif pada fase menunjukkan jeda, sedang nilai positif menunjukkan gelombang “berangkat lebih awal”.
Gelombang sinus sangat penting dalam bidang fisika karena gelombang ini mempertahankan bentuknya ketika ditambahkan kepada gelombang sinus berfrekuensi sama yang lain walaupun fasenya berbeda. Gelombang ini merupakan satu-satunya fungsi periodik yang memiliki sifat ini. Sifat ini menjadikan gelombang ini bagian penting dalam Analisis Fourier.
Secara umum, fungsi ini dapat memiliki:
- dimensi ruang, x (posisi), dengan frekuensi k (juga disebut nomor gelombang)
- titik tengah amplitudo tidak bernilai nol, D (disebut bias DC)
dengan rumus:
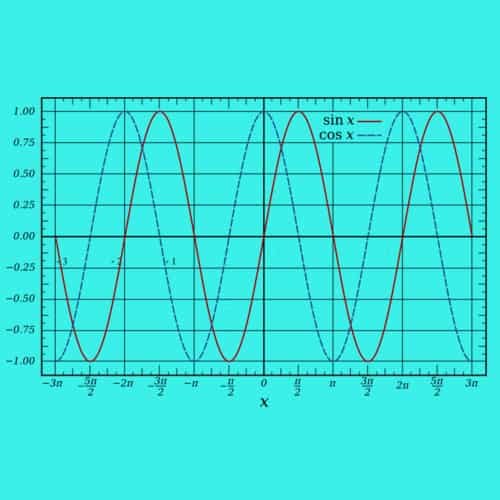
Nomor gelombang bergantung pada frekuensi sudut dengan rumus:
di mana λ adalah panjang gelombang, f adalah frekuensi, dan c adalah kecepatan fase
Persamaan ini menggambarkan gelombang sinus dalam satu dimensi, yaitu persamaan di atas menggambarkan amplitudo gelombang pada posisi x ketika waktu t dalam satu garis saja. Contohnya gelombang pada seutas tali yang digoyang-goyangkan.
Untuk gelombang yang lebih rumit, seperti gelombang air yang terbentuk dari batu yang dilempar kedalam kolam, maka diperlukan rumus yang lebih rumit juga.
Contoh Soal dan Jawaban Gelombang Sinus
1. Jika diketahui suatu gelombang untuk mencapai bentuk gelombang yang sempurna (1 periode) memerlukan waktu selama 0,001 detik, maka berapakah nilai frekuensi gelombang tersebut?
Diketahui : T = 0,001 detik = 10-3 detik
Ditanya : ƒ = ?
Jawab :
ƒ=1/T
= 1/ 10-3 detik
= 10³/detik
ƒ=1000Hz=1LHz
2. Jika panjang gelombang sinusoidal di atas adalah 80 cm maka titik yang memiliki beda fase 3/4 adalah…
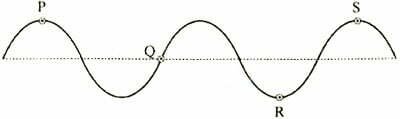
A. P dengan Q
B. P dengan R
C. P dengan S
D. Q dengan S
E. R dengan S
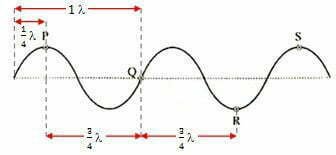
Jika panjang gelombang sinusoidal di atas adalah 80 cm maka titik yang memiliki beda fase 3/4 adalah P-Q dan Q-R. Jawaban: A) Gelombang P dengan A.
3. Jika suatu gelombang memiliki nilai frekuensi sebesar 300 KHz, berapakah panjang gelombang-nya?
Diketahui : ƒ = 300 KHz = 300 x 103 Hz
Ditanya : λ = ?
Jawab :
λ = c / ƒ
= (300×106 m/s) / (300×103 Hz)
λ = 103 m = 1000 m = 1 Km
4. Disediakan 2 pipa organa yang satu terbuka dan yang lain tertutup masing-masing dengan panjang yang sama. Jika cepat rambat bunyi di udara 340 m.s−1 maka perbandingan frekuensi nada atas kedua pipa organa terbuka dengan frekuensi nada atas kedua pipa organa tertutup adalah…
A. 2 : 1
B. 3 : 2
C. 4 : 5
D. 5 : 6
E. 6 : 5
Pembahasan:
Diketahui:
v = 340 m.s-1
l1 = l2
Ditanyakan: f2 terbuka : f2 tertutup = …?
Jawaban:
Frekuensi terbuka dapat kita tentukan dengan rumus:
fn = ½ (n + 1) v/l
f2 = ½ (2 + 1) v/l
f2 = 3/2 v/l
Sedangkan frekuensi tertutup dapat kita tentukan dengan rumus:
fn = ¼ (2n + 1) v/l
f2 = ¼ (2 . 2 + 1) v/l
f2 = 5/4 v/l
Setelah ketemu kedua frekuensi tersebut, sekarang kita bandingkan keduanya.
f2 terbuka : f2 tertutup = 3/2 : 5/4 = 6 : 5
Jadi, perbandingan frekuensi nada atas kedua pipa organa terbuka dengan frekuensi nada atas kedua pipa organa tertutup adalah 6 : 5. Jadi jawabannya adalah E. 6 : 5.
5.Diberikan dua persamaan gelombang bepergian pada seutas tali:
y = 0,04 sin (2πx + 10πt)
y = 0,04 sin (2πx – 10πt)
dengan y dan x dalam m dan t dalam detik. Temukan besarnya amplitudo gelombang berdiri yang dibentuk oleh dua gelombang ini untuk x = 1/12 m!
Jawaban:
Kedua gelombang sinusoidal ini memiliki panjang gelombang dan amplitudo yang sama dan bergerak dalam arah yang berlawanan. Yang pertama adalah ke kiri, yang kedua ke arah rigth. Dengan menerapkan prinsip superposisi kita akan mendapatkan persamaan gelombang berdiri:
y = 2A sin kx cos ω t
jadi kita harus mendapatkan jumlah yang dibutuhkan dari keduanya di atas:
A = 0,04 m
ω = 10π
k = 2π
demikian persamaan kita menjadi
y = 2 (0,04) sin 2πx cos 10π t
y = 0,08 sin 2πx cos 10π t
0,08 sin 2πx itulah yang kita sebut amplitudo gelombang berdiri (As). Untuk x = 1/4 m
As = 0,08 sin 2πx
As = 0,08 sin 2π (1/12)
As = 0,08 sin (π / 6)
As = 0,08 (0,5) = 0,04 m
6. Diberikan sebuah persamaan gelombang Y = 0,02 sin (10πt − 2πx) dengan t dalam sekon, Y dan x dalam meter. Tentukan:
a. amplitudo gelombang
b. frekuensi sudut gelombang
c. tetapan gelombang
d. cepat rambat gelombang
e. frekuensi gelombang
f. periode gelombang
g. panjang gelombang
h. arah rambat gelombang
i. simpangan gelombang saat t = 1 sekon dan x = 1 m
j. persamaan kecepatan gelombang
k. kecepatan maksimum gelombang
l. persamaan percepatan gelombang
m. nilai mutlak percepatan maksimum
n. sudut fase saat t = 0,1 sekon pada x = 1/3 m
o. fase saat t = 0,1 sekon pada x = 1/3 m
c. k = 2π
d. v = ω/k = 10π/2π = 5 m/s
j. v = ω A cos(ωt−kx)=10π(0,02) cos(10πt−2πx) m/s
k. vmaks = ωA = 10π(0,02) m/s
l. a = −ω2y=−(10π)2 (0,02)sin(10πt−2πx) m/s2
m. amaks =|−ω2A|=|−10π2 (0,02)| m/s2
n. sudut fase θ = (10.π.0,1−2π.(1/3)=1/3 π = 60o
o. fase φ = 60o/360o = 1/6
7. Suatu gelombang berjalan melalui titik A dan B yang berjarak 8 cm dalam arah dari A ke B. Pada saat t = 0 simpangan gelombang di A adalah 0. Jika panjang gelombangnya adalah 12 cm dan amplitudonya = 4 cm, tentukan simpangan titik B pada saat fase titik A 3π/2!
Jawaban:
Persamaan gelombang berjalan untuk titik B:
YB = A sin 2π ( t/T − x/λ)
2 π t/T = 3π/2
t/T = 3/4
YB = 4 sin 2π ( 3/4 − 8/12)
YB = 4 sin 2π ( 9/12 − 8/12)
YB = 4 sin ( π/6 ) = 4 sin 30° = 4 ( 0.5) = 2 cm
8. Dua balok kayu kecil A dan B terapung di permukaan danau. Jarak keduanya adalah 150 cm. Ketika gelombang sinusoida menjalar pada permukaan air, teramati bahwa pada saat t = 0 detik, balok A berada di puncak sedangkan balok B berada di lembah. Keduanya dipisahkan satu puncak gelombang. Pada saat t = 1 detik, balok A berada di titik setimbang pertama kali dan sedang bergerak turun. Pernyataan yang benar tentang gelombang pada permukaan air tersebut adalah…
Frekuensi gelombang adalah 0,25 Hz.
Amplitudo gelombang adalah 75 cm.
Pada saat t = 1 detik, balok B berada di titik setimbang dan sedang bergerak turun.
Balok A akan kembali berada di puncak pada saat t = 4,5 detik.
Gelombang air memiliki panjang 200 cm.
Jawaban:
Diketahui:

Ditanya:
Pernyataan yang benar tentang gelombang pada permukaan air?
Pembahasan:
Untuk bisa memperoleh jawaban yang tepat, kita harus terlebih dahulu menghitung satu per satu sesuai pilihan jawaban yang ada.
a. Mencari panjang gelombang:

Ternyata, panjang gelombang air adalah 100 cm, bukan 200 cm. Jadi, pilihan jawaban E salah.
b. Mencari periode:
![]()
c. Mencari frekuensi:
![]()
Jadi, pernyataan yang benar tentang gelombang pada permukaan air tersebut adalah besarnya frekuensi gelombang 0,25 Hz (A).
9. Sebuah gelombang transversal merambat yang menurut persamaan y = 0,5 sin (8πt – 2πx) m.
Tentukanlah arah gelombang dan Amplitudo gelombangnya!
Jawaban:
Arah gelombang ( sumbu x +) karena persamaan bertanda negatif maka gelombang bergerak ke arah kanan sedangkan amplitudo gelombangnya adalah A = 0,5 m
10.Fungsi gelombang sebuah gelombang sinusoidal yang merambat pada tali adalah y (x,t)=0,03 sin (3,5t-2,2x), dengan x dan y dalam meter dan t dalam sekon. hitunglah amplitudo, panjang gelombang, frekuensi, periode dan laju gelombangnya!
Jawaban:
Y(x, t) = A sin (ωt – kx)
y(x, t) = 0,03 sin (3,5t – 2,2x)
Amplitudo
A = 0,03
Panjang gelombang
k = (2π) / λ → λ = (2π) / k
λ = (2π) / 2,2 = 10/11 π
Frekuensi
ω = 2πf → f = ω / (2π)
f = 3,5 / (2π) = 7 / (4π)
Periode
T = 1/f
= 1 / [7 / (4π)] = (4π) / 7
Laju gelombang
v = ω / k
= 3,5 / 2,2 = 35 / 22
Rumus Fisika Lainnya
Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).
Bacaan Lainnya
- Rumus Panjang Gelombang Dan Contoh-Contoh Soal Beserta Jawabannya
- Gelombang Bunyi – Rumus dan Contoh-Contoh Soal Beserta Jawabannya
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
- Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
- Cara Menghentikan Penindasan Bullying
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- 10 Cara Memotivasi Anak Untuk Belajar Agar Menjadi Pintar
- Di Indonesia, (HAN) Hari Anak Nasional tanggal 23 Juli
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Physics, Tutor Vista
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing