Fraktal Geometri

Fraktal Geometri, berkaitan dengan objek terfragmentasi dalam ruang metrik. Fraktal Geometri merupakan pendekatan pertama kurva, permukaan, volume bentuk tidak teratur atau terfragmentasi yang dibuat dengan mengikuti aturan deterministik atau stokastik menyiratkan homothety internal. Istilah “fraktal” ini adalah neologisme (kata baru atau baru muncul dalam bahasa) yang diciptakan oleh ahli matematika Benoît Mandelbrot pada tahun 1974 dari akar kata Latin fractus, yang berarti rusak, tidak beraturan.

Objek pecahan memiliki struktur spasial tidak beraturan yang terfragmentasi tak terhingga, dan dimensi topologi yang belum tentu bilangan bulat, tidak seperti objek biasa. Objek pecahan memiliki dimensi Hausdorff lebih besar dari dimensi topologinya. Objek fraktal adalah objek pecahan yang juga memiliki struktur spasial yang mengikuti aturan deterministik atau probabilistik yang melibatkan kesamaan diri internal. Geometri fraktal mengkaji objek fraktal geometris. Artikel ini membahas geometri ini, dan memberikan daftar aplikasi praktis, dengan kasing yang terperinci (Lorenz penarik).

Kata “fraktal” berasal dari bahasa latin “fractus” yang berarti “patah”. Memang, fraktal adalah objek geometris “terfragmentasi tak terhingga” yang detailnya dapat diamati pada skala yang dipilih secara sewenang-wenang.
Dengan memperbesar bagian dari gambar, kita dapat menemukan keseluruhan gambar, kita mengatakan bahwa itu serupa.

Meskipun beberapa hal sudah diketahui, penemuan fraktal dikaitkan dengan seorang politeknik Prancis, Benoît Mandelbrot (1924; 2010).
Penelitian pertamanya dimulai pada tahun 1964 ketika ia menggunakan istilah self-similar dalam sebuah penelitian yang dilakukan di IBM. Tetapi pada tahun 1975 ia memamerkan karyanya dan memberi nama “fraktal” dalam bukunya “Fractal Objects”.

Fraktal dalam banyak bidang

Bentuk fraktal kasar mudah terlihat di alam. Teori matematika fraktal dapat memberikan informasi menarik dalam beberapa bidang ilmiah seperti:

dalam geologi, studi bantuan, pantai dan aliran air, struktur batuan, longsoran;
dalam morfologi hewan, struktur invertebrata, bulu burung;
dalam kedokteran, struktur paru-paru, usus, detak jantung;
dalam meteorologi, awan, vortisitas, gumpalan es, gelombang jahat, turbulensi, struktur petir;
dalam vulkanologi, peramalan letusan gunung berapi, gempa bumi;
dalam astronomi dengan deskripsi struktur alam semesta, kawah di Bulan, distribusi galaksi;
dalam ilmu manusia, struktur perkotaan, evolusi demografi;
di bidang ekonomi, peramalan crash pasar saham.

Contoh Fraktal Geometri sederhana dan teratur dengan ilustrasi

Fraktal Geometri	Sytem L	Sudut	Rasio jarak	Visualisasi	jumlah Sumbu cermin	Titik simetri	Simetri rotasi	Dimensi
Kurva layang-layang	F → R or F → L R → + R - L + L → -R ++ L-	45°	1: 1/√2		0	Tidak ada	Tidak ada	2
Kurva gosper	F → R or F → L R → R + L ++ LR - RR-L + L → -R + LL ++ L + R - RL	60°	1: 1/√7		0	Ada	6 angka	2
Kurva Hilbert	X X → -YF + XFX + FY- Y → + XF-YFY-FX +	90°	1: ½		1	Tidak ada	Tidak ada	2
Serpihan Koch	F - F - F F → F + F - F + F	60°	1: ⅓		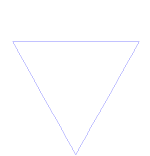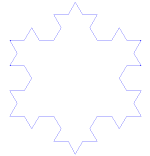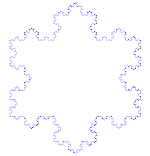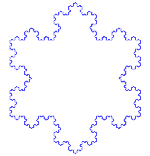12	Ada	6 angka	2
Kurva Peano	X X → XFYFX + F + YFXFY-F-XFYFX Y → YFXFY-F-XFYFX + F + YFXFY	90°			0	Ada	2 angka	2
Kurva Peano	F. F → F-F + F + F + FFF-F + F	90°	1: ⅓		0	Ada	2 angka	2
Penta Plexity	F ++ F ++ F ++ F ++ F F → F ++ F ++ F | F-F ++ F	36°	1: 1/{(√5+1) / (2)}²		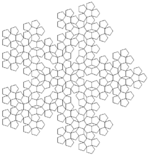10	Tidak ada	5 angka	2
Mata panah (Arrowhead)	F → R or F → L R → -L + R + L- L → + RL-R +	60°	1: ½		1	Tidak ada	Tidak ada	2
Segitiga Sierpinski	FXF - FF - FF X → --FXF ++ FXF ++ FXF-- F → FF	60°			6	Tidak ada	3 angka	2
Segitiga Sierpinski, varian ke-2	F - F - F F → F - F - F - ff f → ff	60°	1: ⅓		6	Tidak ada	3 angka	2
Karpet Sierpinski	F. F → F + FF-FF-FF-fF f → fff	90°	1: ⅓		8	Ada	4 angka	2
Kurva Levy C	F. F → + F - F +	45°	1: 1/√2		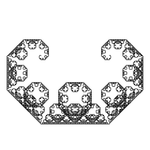1	Tidak ada	Tidak ada	2

Penjelasan tentang sistem-L (sistem Lindenmayer)

The opsional , yaitu tidak perlu, F umumnya digunakan sebagai rute yang diganti dengan urutan instruksi. Seperti F , huruf besar lainnya seperti R dan L berarti bagian dari rute yang sedang diganti. + dan – mewakili sudut tertentu yang berjalan searah atau berlawanan arah jarum jam. Simbol | mengacu pada putaran U pensil, yaitu putaran sebesar 180 °. Jika perlu, kelipatan sudut rotasi yang sesuai digunakan untuk ini.

Contoh kurva layang-layang

F → R
R → + R – L +
L → -R ++ L-

F adalah jarak sederhana antara dua titik. F → R berarti segmen F digantikan oleh R. Langkah ini diperlukan karena memiliki dua penggantian rekursif, R dan L, yang saling mengandung. Berikut ini diganti sebagai berikut:

R.
+ R – L +
+ (+ R – L +) – (- R ++ L -) +
+ (+ (+ R – L +) – (- R ++ L -) +) – (- (+ R – L +) ++ (- R ++ L -) -) +
.
.
.

Dari bagian tertentu proses penggantian ini harus dibatalkan untuk mendapatkan grafik:

+ (+ (+ r – l +) – (- r ++ l -) +) – (- (+ r – l +) ++ (- r ++ l -) -) +

Di sini, r dan l masing-masing mewakili rute tetap.

Contoh Soal dan Jawaban

1. Fraktal telah menjadi jauh lebih populer sejak munculnya komputasi elektronik karena mereka bergantung pada aspek komputasi apa?

A. kemampuan untuk dengan cepat membuat dan membuat grafik kumpulan data formula yang besar dan kompleks
B. tingkat iterasi dan rekursi yang tinggi
C. semua ini
D. sejumlah besar perhitungan

Jawaban: semua ini

Masalah fraktal telah disentuh sejak awal abad ke-17 tetapi sebagian besar pekerjaan paling awal di daerah itu terhalang oleh jumlah perhitungan berulang yang diperlukan. Faktanya, beberapa formula paling awal di bidang ini disebut sebagai “monster” matematika karena sifatnya yang sulit digunakan.

2. Fraktal terkait erat dan sering dianggap sebagai bagian dari bidang Matematika apa?

A. Kombinatorik
B. Kemungkinan
C. Teori Permainan
D. Geometri

Jawaban: Geometri

Fraktal adalah pola kompleks tak terhingga yang serupa diri di seluruh skala yang berbeda Istilah “fraktal” itu sendiri berasal dari gagasan memecah garis atau gambar menjadi contoh yang lebih kecil tetapi serupa dari aslinya. Secara konseptual, ini dilakukan berulang-ulang, ad-infinitum menghasilkan set tak terbatas.

Combinatorics berurusan terutama dengan menghitung dan set. Teori permainan terutama berkaitan dengan strategi antara pembuat keputusan rasional (seringkali dalam permainan zero-sum). Probabilitas berkaitan dengan peluang hasil tak tentu (misalnya peluang & perjudian)

3. Apa matematikawan yang menciptakan kata fraktal dan kadang-kadang menyebut dirinya sebagai “fraktalis?”

Rene Descartes
Pierre de Fermat
Daniel Bernoulli
Benoit Mandelbrot

Jawaban: Benoit Mandelbrot

Dikenal karena bakatnya untuk penelitian praktis, Mandelbrot dan afinitas komputer, lahir sebagai seorang Yahudi Polandia, menjadi karyawan IBM pada tahun 1958. Dia adalah salah satu orang pertama yang menggunakan grafik komputer untuk membuat dan menampilkan gambar geometris fraktal yang menampilkan “seni kekasaran. ”

4. Benoit Mandelbrot mulai berkonsentrasi pada fraktal ketika dia diminta untuk melihat masalah yang dialami IBM. Apa yang menjadi perhatian masalah?

peningkatan bug saat program bertambah panjang
kebisingan dalam transmisi sinyal masuk
kesalahan dalam algoritma terjemahan bahasa
panas yang dihasilkan oleh komputer mainframe besar

Jawaban: kebisingan dalam transmisi sinyal masuk

Mandelbrot membuat grafik tingkat kebisingan dan memperhatikan bahwa grafik tampak hampir identik terlepas dari skala waktu. Itu mengingatkannya pada kesamaan diri yang dia dengar dengan “monster.”

5. Manakah perangkat konsumen yang umum digunakan ini yang menggunakan fraktal?

pemutar DVD
telepon seluler
oven microwave
kalkulator digital

Jawaban: telepon seluler

Sebagian besar telepon seluler menggunakan antena yang didasarkan pada desain fraktal. Sifat rekursif dari kesamaan diri yang diperlukan dari nilai fraktal cukup banyak menjamin berbagai panjang efektif yang berarti bahwa mereka dapat menangani spektrum frekuensi sinyal yang luas dalam footprint yang lebih kecil daripada desain antena lainnya.

6. Pada tahun 1904 salah satu fraktal paling awal dan paling sederhana dideskripsikan oleh Helge von Koch, “Koch Snowflake.”
Kepingan salju ini didasarkan pada bentuk geometris standar apa?

sebuah lingkaran
sebuah tesseract
sebuah persegi
segitiga sama sisi

Jawaban: segitiga sama sisi

Untuk membuat kepingan salju Koch, Anda perlu melakukan hal berikut:

1) Mulailah dengan segitiga sama sisi.

2) Sekarang bagi masing-masing kaki segitiga itu menjadi tiga bagian yang sama dan ganti sepertiga tengah dengan dua segmen garis dengan panjang itu yang membentuk segitiga sama sisinya sendiri (tanpa alas), mengarah ke luar dari bentuk aslinya.
Ini harus menjadi bentuk enam runcing yang mirip dengan “Bintang Daud.” Bukan berarti keliling bentuk yang dihasilkan adalah 4/3 dari panjang keliling aslinya.

3) Membagi setiap segmen garis yang dihasilkan menjadi tiga bagian dan mengulanginya
proses ini akan menghasilkan angka yang memiliki 18 poin dan mulai menyerupai kepingan salju

4) Iterasi keempat akan menghasilkan angka dengan 54 poin, kemudian 162, 486 dan seterusnya..

Setiap iterasi menghasilkan angka yang memiliki keliling 4/3s dari panjang gambar sebelumnya dan dengan cepat menjadi jelas bahwa, saat iterasi berlanjut, keliling akan mendekati tak terhingga meskipun area tertutup tetap terbatas.

7. Fraktal yang sedikit lebih kompleks dimulai dengan segitiga sama sisi tegak lurus dan membaginya menjadi empat segitiga sama sisi dengan menghubungkan titik tengah ketiga sisinya membentuk segitiga sama sisi bagian dalam yang terbalik.
Melakukan proses ini secara rekursif untuk setiap segitiga yang dihasilkan menghasilkan gambar yang mulai terlihat seperti gasket. Disebut apakah angka fraktal ini?

buaian kucing
sebuah Kubus Rubik
segitiga sierpinski
penarik yang aneh

Jawaban: Segitiga Sierpinski

Segitiga Sierpinski juga kadang-kadang disebut paking Sierpinski atau saringan Sierpinski. Ini pertama kali disusun oleh Wac³aw Sierpiñski pada tahun 1915. Meskipun paling jelas ketika dimulai dengan segitiga sama sisi, bentuk awal lainnya dapat digunakan dalam transformasi ini. Sebagian besar antena ponsel modern didasarkan pada salah satu jenis fungsi ini.

8. Manakah dari berikut ini yang BUKAN merupakan contoh yang baik tentang bagaimana fraktal muncul di alam?

A. kepingan salju
B. pola percabangan pohon
C. garis-garis pada zebra
D. garis pantai

Jawaban: garis-garis pada zebra

Garis-garis pada zebra pada dasarnya teratur dan mencerminkan pola pertumbuhan rumput. Jika dilihat lebih dekat, mereka tidak menunjukkan aspek “kemiripan diri” dari fraktal.

Sebaliknya, memperbesar kepingan salju, garis pantai, dan cabang pohon semuanya menghasilkan gambar yang menunjukkan kesamaan dengan gambar yang diperkecil.

9. Menerapkan aturan yang ditetapkan secara rekursif untuk masalah tertentu terjadi di beberapa permainan asah otak. Membuat diagram solusi terpendek dan terlama terkadang akan menghasilkan angka yang terlihat luar biasa seperti pada fraktal yang telah kita diskusikan. Teka-teki populer mana yang merupakan contoh dari itu?

1-15 Teka-teki Angka Geser
Teka-teki Simpul Gordian
Kunci dalam Puzzle Botol
Teka-teki Menara Hanoi

Jawaban:

Teka-teki Menara Hanoi

Dalam teka-teki Tower of Hanoi, pemain harus memindahkan disk dari satu tongkat ke tongkat lainnya pada satu waktu dengan tunduk pada aturan. Dalam versi standar, setiap gerakan harus mengambil hanya satu disk dari tumpukan dan meletakkannya di atas tumpukan lain dan tidak ada disk yang lebih besar yang boleh ditempatkan di atas disk yang lebih kecil.

Dalam solusi lengkap dari teka-teki ini, setiap disk akan bergerak hanya setengah dari disk tepat di atasnya dan memplot gerakan dengan ketinggian disk yang dipindahkan menciptakan bentuk seperti fraktal (walaupun itu hanya akan menjadi fraktal sejati untuk sebuah teka-teki ketinggian tak terbatas).

10. Persamaan berbasis fraktal telah ditemukan berguna dalam semua aplikasi ini kecuali satu. Yang?

A. membuat efek CGI film
B. menentukan jalur optimal dalam situasi lalu lintas jalan raya
C. menentukan panjang garis pantai
D. pemodelan sistem peredaran darah manusia

Jawaban: menentukan jalur optimal dalam situasi lalu lintas jalan raya

Loren Carpenter dari Pixar Studios menggunakan fraktal pada komputer berkecepatan rendah untuk mensimulasikan pegunungan ketika bekerja di perusahaan Boeing dan sekali lagi di Lucasfilm dalam mengembangkan urutan CGI sepenuhnya pertama di dunia untuk film fitur, “Star Trek II: The Wrath of Khan”. Mandelbrot awalnya mempresentasikan karyanya dalam makalah “Berapa Panjang Pantai Inggris?.” Percabangan berulang seperti pada pohon, penempatan daun pada pakis, dan pembuluh darah dalam sistem peredaran darah semuanya telah berhasil dimodelkan menggunakan fungsi fraktal.

Masalah lalu lintas jalan raya tidak melibatkan aspek yang sama dari kekasaran alami di mana fraktal unggul. Mereka cenderung lebih terkait dengan probabilitas.

Jenis dan Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan

Sumber bacaan: Cleverly Smart, Britannica, Hidden Dimension, Sporcle

Sumber foto: Johannes Rössel / Wikimedia Commons (Public Domain)

Penjelasan foto: Karpet Sierpinski (ke level 6), fraktal dengan dimensi topologi 1 dan dimensi Hausdorff 1,893.

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing