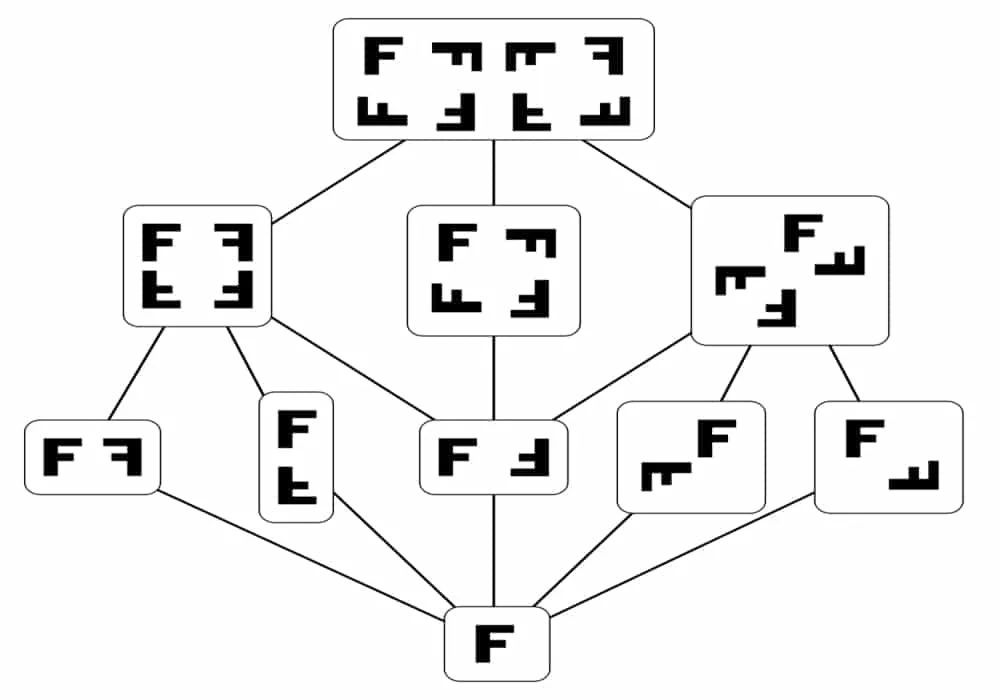
Aksi Grup Matematika

Dalam matematika, aksi grup adalah suatu himpunan, beserta satu operasi biner, seperti perkalian atau penjumlahan, yang memenuhi beberapa aksioma yang disebut aksioma grup. Misalnya, himpunan bilangan bulat adalah suatu grup terhadap operasi penjumlahan. Cabang matematika yang mempelajari grup disebut teori grup.

Notasi Aksi Grup

Suatu grup yang terdiri atas himpunan $G$ dan operasi $*$ dapat ditulis $(G,*)$ .

Biasanya operasi dalam grup, apa pun sebetulnya operasi tersebut, dipikirkan sebagai analog dari perkalian, dan operasi grup ditulis seperti perkalian (notasi perkalian):

Kita menulis $a\cdot b$ , atau bahkan $ab$ , untuk $a*b$ .
Kita menulis $1$ untuk unsur identitas dan menyebutnya unsur satuan.
Kita menulis $a^{-1}$ untuk invers $a$ dan menyebutnya kebalikan dari $a$ .

Tetapi, kadang-kadang operasi grup dipikirkan sebagai analog dari penjumlahan dan ditulis seperti penjumlahan (notasi penjumlahan):

Kita menulis $a+b$ untuk $a*b$ dan menyebutnya jumlah $a$ dan $b$ .
Kita menulis $0$ untuk unsur identitas dan menyebutnya unsur nol.
Kita menulis $-a$ untuk invers $a$ dan menyebutnya lawan dari $a$ .

Biasanya, hanya grup abelian (grup yang operasinya komutatif untuk setiap dua unsur himpunan grup tersebut) yang ditulis dalam bentuk penjumlahan walaupun grup tersebut dapat juga ditulis dalam bentuk perkalian. Ketika bersifat noncommittal, kita dapat menggunakan notasi (dengan $*$ ) dan istilah yang dikemukakan dalam definisi menggunakan notasi $a^{-1}$ sebagai invers dari $a$ .

Bila $S$ adalah sub himpunan dari $G$ dan $x$ unsur dari $G$ maka dalam notasi perkalian $xS$ merupakan himpunan dari semua hasil perkalian $xs$ untuk $s$ dalam $S$ (dengan kata lain, $xS=\{xs|s\in S\}$ ). Hal yang sama juga dapat dilihat pada notasi $Sx=\{sx|s\in S\}$ , dan untuk dua sub himpunan $S$ dan $T$ dari $G$ kita dapat menulis $ST$ untuk $\{st|s\in S,t\in T\}$ . Dalam notasi penjumlahan, kita menuliskan $x+S,S+x,$ dan $S+T$ untuk masing-masing pasangan.

**Suatu aksi grup adalah suatu himpunan $G$ beserta satu operasi biner $$ yang memenuhi aksioma-aksioma grup* berikut**

Ketertutupan (closure) : untuk setiap $a,b\in G$ , berlaku $a*b\in G$ .
Sifat asosiatif : untuk setiap <<< $a,b,c\in G$ , berlaku $(a*b)*c=a*(b*c)$ .
Unsur identitas : terdapat suatu $i\in G$ sehingga untuk setiap $a\in G$ berlaku $a*i=i*a=a$ (dapat dibuktikan bahwa dalam grup manapun hanya terdapat satu unsur identitas).
Unsur invers : untuk setiap $a\in G$ , terdapat suatu $b\in G$ sehingga $a*b=b*a=i$ , di mana $i$ adalah unsur identitas (dapat dibuktikan bahwa setiap unsur $G$ memiliki tepat satu unsur invers).

Aksi grup matematika. Kisi-kisi subkelompok grup dihedrum Dih4, direpresentasikan sebagai kelompok rotasi dan refleksi dari sosok gambar ini. Sumber foto: Wikimedia Commons

Beberapa Contoh Elemen dan Bukan Contoh Elemen

Sebuah grup abelian : bilangan bulat terhadap penjumlahan

Contoh grup yang pernah diperkenalkan saat di sekolah dasar salah satunya adalah bilangan bulat terhadap penjumlahan. Misalkan “’Z”’ merupakan himpunan bilangan bulat, {…, -4, -3, -2, -1, 0, 1, 2, 3, 4,…} dan simbol “+” sebagai operasi penjumlahan. Dengan demikian, (“’Z”’,+) merupakan suatu grup.

Bukti :

    * Bila “a” dan “b” merupakan bilangan  bulat maka “a” + “b” juga merupakan bilangan bulat.
    *Bila “a”, “ b”, dan “c” adalah bilangan bulat maka (“a” + “b”) + “c”  = “ a” + (“b”+”c”) (sifat asosiatif)
    *0 adalah bilangan bulat dan untuk setiap bilangan bulat “a”,  0 +” a” = “a”. (elemen identitas)
    *Bila  “a”  sebuah bilangan bulat maka terdapat bilangan bulat “b” = -“a” sedemikian   sehingga “a” + “b”  =  “b” +” “a = 0 (elemen invers)

Grup ini juga merupakan abelian : “a” +” b” = “b” + “a”.

Bilangan bulat terhadap penjumlahan dan perkalian membentuk struktur aljabar cincin yang lebih kompleks. Sebenarnya, elemen dari cincin apa saja membentuk sebuah grup abelian terhadap penjumlahan yang disebut “grup penjumlahan” dari cincin.

“Bukan” grup : bilangan bulat terhadap perkalian

Bilangan bulat terhadap perkalian yang dilambangkan dengan “ “’ ×’” ” Maka (“’Z’”, “’ ×’” ) bukan sebuah grup :

       *Bila “a” dan “b” bilangan bulat maka “a” “’ ×’”  “b” merupakan bilangan bulat
       *Bila “a”, “b”, dan “c” bilangan bulat maka (“a”“’ ×’”  “b”) “’ ×’” “c” = “a”“’ ×’” (“b”“’ ×’” “c”) (sifat asosiatif)
       *1 adalah bilangan bulat dan untuk setiap bilangan bulat “a”, 1 “’ ×’” “a” = “a”“’ ×’” 1 = “a” (elemen identitas)
       *Tetapi, bila “a” sebaramg bilangan bulat bukan 0 maka tidak ada bilangan bulat  
        bukan 0 yang memenuhi “a””b” = “b””a” = 1. Sebagai contoh, misalkan “a” = 2 maka 
        berapapun “b” (bilangan bulat bukan 0) maka |”a””b”| = |2”b”| ³2 > 1. (elemen invers tidak memenuhi)

Karena tidak semua elemen dari (“’Z’”, “’ ×’”) mempunyai invers maka (“’Z’”, “’ ×’”) bukan merupakan grup. Kita dapat menyebut (“’Z’”, “’ ×’”) sebuah monoid komutatif.

Sebuah grup abelian : bilangan rasional bukan 0 terhadap perkalian

Misalkan “’Q’” sebagai himpunan bilangan rasional, yaitu bilangan yang dapat dinyatakan dengan “a”/”b” dengan “a” dan “b” merupakan bilangan bulat dan”b” bukan nol. Misalkan pula operasi perkalian dinyatakan dengan simbol ““’ ×’” ”. Karena bilangan rasional 0 tidak memiliki invers untuk perkalian maka (“’Q’”, “’ ×’”), sebagaimana juga (“’Z’”, “’ ×’”) bukan sebuah grup.

Akan tetapi, kalau kita menggunakan himpunan “’Q’” \ {0}, yang mencakup setiap bilangan rasional “kecuali nol “ maka (“’Q’”\{0},“’ ×’”) merupakan grup abelian. Invers “a”/”b” adalah “b”/”a” dan aksioma grup lainnya mudah diperiksa kebenarannya. Kita tidak kehilangan closure dengan menghilangkan nol karena hasil kali dua bilangan rasional tidak nol tidak akan pernah nol.

Sama seperti bilangan bulat yang membentuk cincin, demikian juga bilangan rasional yang membentuk struktur aljabar dari bidang. Sebenarnya, elemen bukan nol dari medan apapun akan membentuk grup terhadap perkalian yang disebut “grup perkalian” dari bidang.

Grup bukan belian tertentu : permutasi dari himpunan

Misalkan tiga buah blok berwarna (merah, hijau, dan biru) yang mula-mula diletakkan dengan susunan MHB. Misalkan “a” merupakan aksi “menukarkan blok pertama dan blok kedua” dan “b” aksi “menukarkan blok kedua dan ketiga”.

Dalam bentuk perkalian, kita menuliskan “x””y” untuk aksi “pertama kali lakukan “y” kemudian lakukan “x” ” sehingga “a””b” adalah aksi MHB ®MBH®BMH yaitu “ambil blok terakhir dan pindahkan ke depan”. Bila kita menuliskan “e” untuk aksi “ biarkan blok sebagaimana adanya” (aksi identitas) maka kita dapat menulis 6 permutasi dari himpunan 3 blok sebagai berikut :

   * e : MHB  ®    MHB
   * a : MHB   ®   HMB
   *b :  MHB   ®     MBH
   * ab  : MHB    ®    BMH
   *ba  :  MHB  ®      HBM
   *aba : MHB    ®     BHM

Perhatikan bahwa aksi “a””a” akan menyebabkan MHB ® HMB ® MHB atau aksi tersebut sama saja dengan aksi “biarkan blok sebagaimana adanya”. Dengan demikian, kita dapat menuliskan “a””a” = “e”. Demikian pula,

   * “b””b” = “e”
   *(“a””b””a”)(“a””b””a”) = “e” dan
   *(“a””b”)(“b””a”) = (“b””a”)(“a””b”) = “e”.

Jadi, tiap aksi di atas mempunyai sebuah invers.

Dengan menyelidiki, kita juga dapat menentukan sifat asosiatif dan closure. Sebagai contoh perhatikan,

         *(“a””b”)”a” = “a”(“b””a’) = “a””b””a”, dan
         *(“b””a”)”b” = “b”(“a””b”) = “a””b””a”.

Grup ini disebut simetri grup pada tiga huruf, atau “S”3. Grup tersebut mempunyai orde 6 ( atau 3 “faktorial”), dan bukan merupakan grup abelian (karena sebagai contoh “a””b” ≠ “b””a”). Karena “S”3 dibangun dari aksi dasar “a” dan “b” maka kita dapat mengatakan bahwa himpunan {“a”,”b”} membangun “S”3.

Setiap grup dapat diungkapkan dalam grup permutasi seperti “S”3. Hasilnya merupakan Teorema Cayley dan dipelajari sebgai bagian dari subyek grup.

Contoh lanjutan

Untuk beberapa contoh lanjutan dari grup untuk berbagai aplikasi lihat contoh-contoh grup dan daftar grup kecil.

Teori sederhana

    *Sebuah grup mempunyai hanya satu elemen identitas.
    *Setiap elemen mempunyai hanya satu invers.
    *Kita dapat membagi grup yaitu elemen grup “a” dan “b” dari grup “G”, hanya ada satu solusi “x” dalam “G” terhadap persamaan “x”*”a” =”b” dan hanya satu solusi “y” dalam “G” 
 untuk persamaan “a”*”y” = “b”.
   *Ungkapan “ “a”1*”a”2*...”a”n ”  tidak ambigius karena hasilnya akan sama dimana saja kita menempatkan tanda kurung.
   *Invers perkalian adalah hasil kali invers dalam susunan terbalik : (“a”*”b”)-1 = “b”-1 *”a”-1.

Faktor ini dan faktor dasar lainnya juga berlaku untuk semua grup tertentu yang membentuk bidang dari teori grup elementer.

Contoh Soal dan Jawaban Aksi Grup Matematika

**1. Misalkan G adalah himpunan tak kosong, dan * adalah operasi biner pada G. Himpunan Gdisebut grup jika dan hanya jika**

P1 : Untuk setiap a, b, c di G, berlaku

(a*b)*c = a*(b*c). — operasi * bersifat asosiatif

P2 : Teradapat elemen e di G sedemikian sehingga untuk setiap x di G, berlaku

e*x = x*e = x. — e disebut elemen identitas

P3 : Untuk setiap elemen a di G, terdapat elemen a’ di G sedemikian sehingga

a*a’ = a’*a = e. — a’ disebut invers dari a

Grup G dengan operasi biner * selanjutnya dinotasikan dengan <G,∗>

Contoh-contoh Aksi Grup

Contoh 1

Himpunan bilangan bulat Z dengan operasi biner penjumlahan + merupakan grup, sebab + pada Z memenuhi semua aksioma P1, P2, dan P3. Perhatikan bahwa:

Untuk setiap a, b, c di Z, berlaku

(a + b) + c = a + (b + c)

Dengan demikian, + asosiatif.

Terdapat elemen identitas 0 di Z sedemikian sehingga untuk setiap x di Z, berlaku

0 + x = x + 0 = x.

Untuk setiap elemen a di Z, terdapat elemen –a in Z, yaitu invers dari a, sedemikian sehingga

a + (-a) = (-a) + a = 0.

Contoh 2

Bilangan rasional adalah bilangan yang dapat ditulis dalam bentuk pq dengan p dan q adalah bilangan bulat dan q tidak nol. Himpunan bilangan rasional biasa dinotasikan dengan Q. Kemudian didefinisikan operasi biner perkalian .. Apakah <Q,.> merupakan grup? Berikut uraiannya.

Berdasarkan informasi yang telah kita miliki, sudah dapat dipastikan bahwa operasi . pada Qbersifat asosiatif. Dengan kata lain,

(a.b).c = a.(b.c) untuk setiap a, b, c di Q.

Sayangnya, ada satu elemen yang tidak mempunyai invers, yaitu 0, karena bilangan 10 tidak ada. Selain itu, setiap elemen yang dikalikan dengan 0 sama dengan 0. Dengan demikian, Q bukan grup, karena tidak memenuhi aksioma elemen idenitas.

2. Cek apakah aksi grup atau bukan:
$A= \{ 2^m,m \in Z \}$ $(A, \cdot )$

1) Cek apakah A tertutup terhadap operasi $\cdot$
ambil bilangan $2^{m1}$ dan $2^{m2}$ anggota A
$2^{m1} \cdot 2^{m2}$ = $2^{m1 + m2}$
karena m1 + m2 anggota bilangan bulat Z, maka $2^{m1} \cdot 2^{m2}$ anggota A
Jadi, A tertutup terhadap operasi $\cdot$

2) Cek apakah memiliki unsur identitas (e)
misal kita ambil bilangan $2^m$ anggota A
$2^m \cdot e = 2^m$
$e = \frac{2^m}{2^m} = 2^0$
karena 0 anggota bilangan bulat Z maka e anggota A
Jadi, A memiliki unsur identitas e = $2^0$

3) Cek apakah mempunyai invers untuk setiap unsur dalam A
misal kita ambil bilangan $2^m$ anggota A
$2^m \cdot a' = e = 1$
$a' = 2^{-m}$
karena -m anggota bilangan bulat Z, maka ada invers di dalam himpunan A

4) Cek asosiatif
$( 2^{m1} \cdot 2^{m2} ) \cdot 2^{m3} = 2^{m1} \cdot 2^{m2} \cdot 2^{m3}$
$2^{m1} \cdot (2^{m2} \cdot 2^{m3} ) = 2^{m1} \cdot 2^{m2} \cdot 2^{m3}$
maka,
$( 2^{m1} \cdot 2^{m2} ) \cdot 2^{m3} = 2^{m1} \cdot (2^{m2} \cdot 2^{m3} )$
Jadi, hukum asosiatif terpenuhi

Kesimpulan: $(A, \cdot )$ adalah grup

3. Apakah himpunan bilangan Real dengan operasi tambah (+) adalah grup?
Kita akan mengecek satu persatu syarat sebuah himpunan dikatakan grup.

1) Cek apakah R tertutup terhapad operasi +.
misal kita ambil dua buah bilangan a dan b anggota R
a + b = c,
karena c selalu anggota R maka himpunan R tertutup terhadap operasi +

2) Cek apakah R mempunyai unsur identitas (e)
misal kita ambil sebuah bilangan a anggota R
a + e = a
e = a – a = 0
karena 0 anggota dari R maka himpunan R mempunyai unsur identitas

3) Cek apakah R mempunyai invers (a’) untuk setiap unsur
misal kita ambil sebuah bilangan a anggota R
a + a’ = e
a’ = e – a
a’ = 0 – a
a’ = -a
karena -a adalah anggota R maka setiap unsur dalam R mempunyai invers

4) Cek asosiatif
misal kita ambil a, b, dan c anggota R
(a + b) + c = a + b + c = a + (b + c)
terbukti (a + b) + c = a + (b + c)
maka hukum asosiatif terpenuhi

Jadi, karena keempat syarat terpenuhi, maka himpunan bilangan Real dengan operasi tambah (+) adalah grup.

**4. Pada himpunan bilangan bulat ( $\mathbb{Z}$ ) didefinisikan operasi $*$ , yaitu**

**$a*b=a+b+1, \quad \forall a,b \in \mathbb{Z}$**

**Periksa apakah $(\mathbb{Z},*)$ merupakan grup.**

Pembahasan:

Kita dapat memeriksa apakah $\mathbb{Z}$ bersifat tertutup terhadap operasi $*$ .
Ambil sebarang $a,b \in \mathbb{Z}$ . Perhatikan bahwa

$a*b=a+b+1$

Jumlah tiga bilangan bulat merupakan bilangan bulat, sehingga $a*b \in \mathbb{Z}$ .
Jadi, $\mathbb{Z}$ bersifat tertutup terhadap operasi $*$ .

Kita akan memeriksa apakah $*$ merupakan operasi yang bersifat asosiatif.
Ambil sebarang $a,b,c \in \mathbb{Z}$ . Perhatikan bahwa

$\begin{align*} a*(b*c) &= a*(b+c+1) &\text{[Definisi operasi } *] \\ &= a + (b+c+1) + 1 &\text{[Definisi operasi } *] \\ &= a+b+c+(1+1) &\text{[Operasi + asosiatif]} \\ &= a+b+c+2 \end{align*}$

di lain pihak

$\begin{align*} (a*b)*c &= (a+b+1)*c &\text{[Definisi operasi } *] \\ &= (a+b+1) + c + 1 &\text{[Definisi operasi } *] \\ &= a+b+(1+c)+1 &\text{[Operasi + asosiatif]} \\ &= a+b+(c+1)+1 &\text{[Operasi + komutatif]} \\ &= a+b+c+(1+1) &\text{[Operasi + asosiatif]} \\ &= a+b+c+2 \end{align*}$

Diperoleh $a*(b*c)=(a*b)*c$ .
Jadi, $\mathbb{Z}$ bersifat asosiatif terhadap operasi $*$ .

5. Periksa apakah himpunan bilangan bulat ( $\mathbb{Z}$ ) dengan operasi penjumlahan biasa merupakan grup.

Pembahasan:

Kita dapat memeriksa apakah $\mathbb{Z}$ bersifat tertutup terhadap operasi $+$ .
Ambil sebarang $a,b \in \mathbb{Z}$ . Jumlah dua bilangan bulat merupakan bilangan bulat, sehingga $a+b \in \mathbb{Z}$ .
Jadi, $\mathbb{Z}$ bersifat tertutup terhadap operasi $+$ .
Kita akan memeriksa apakah operasi $+$ bersifat asosiatif.
Ambil sebarang $a,b,c \in \mathbb{Z}$ . Perhatikan bahwa $a+(b+c)=(a+b)+c$ .
Jadi, operasi $+$ bersifat asosiatif.
Kita akan memeriksa apakah $(\mathbb{Z},*)$ mempunyai unsur identitas.
Terdapat $0 \in \mathbb{Z}$ sehingga untuk setiap $a \in \mathbb{Z}$ berlaku $a+0=a$ dan $0+a=a$ .
Jadi, $0$ merupakan unsur identitas pada $(\mathbb{Z},+)$ .
Kita akan memeriksa apakah setiap $a \in \mathbb{Z}$ mempunyai invers.
Untuk setiap $a \in \mathbb{Z}$ terdapat $-a \in \mathbb{Z}$ sehingga $a+(-a)=0$ dan $(-a)+a=0$ .
Jadi, setiap unsur di $\mathbb{Z}$ mempunyai invers.