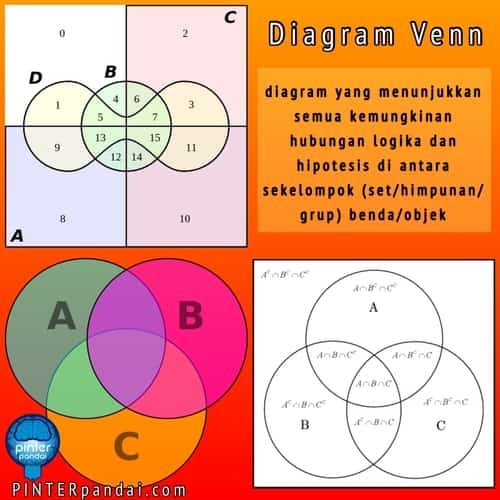
Diagram Venn
Diagram Venn adalah gambar yang digunakan untuk mengekspresikan hubungan antara himpunan dalam sekelompok objek yang memiliki kesamaan nilai atau jumlah.
Pelajari metode dan jalan pintas untuk menjawab pertanyaan-pertanyaan pada Diagram Venn. Diagram Venn, juga dikenal sebagai diagram Euler-Venn adalah representasi sederhana dari himpunan oleh diagram. Penggambaran biasa menggunakan persegi panjang sebagai set universal dan lingkaran untuk set yang dipertimbangkan.
Apa nama bagian tengah dari diagram Venn?
dalam urutan tiga diagram Venn dalam kasus khusus dari pusat masing-masing yang terletak di persimpangan dua lainnya adalah bentuk geometris yang dikenal sebagai segitiga Reuleaux.
Baca juga: Rumus Himpunan Matematika Beserta Soal dan Jawaban
Rumus Diagram Venn
Mari kita lihat beberapa rumus dasar untuk diagram Venn dari dua dan tiga elemen.
n (A ∪ B) = n (A) + n (B) – n (A∩ B)
n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n (A ∩ B) – n (B ∩ C) – n (C ∩ A) + n (A ∩ B ∩ C)
Dan seterusnya, di mana n (A) = jumlah elemen dalam himpunan A.
Setelah Anda memahami konsep diagram Venn dengan bantuan diagram, Anda tidak perlu mengingat rumus ini.
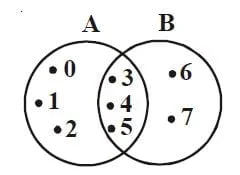
Diagram Venn jika terdiri dari dua elemen

Dari gambar di atas, jelas terlihat
n (A) = x + z;
n (B) = y + z;
n (A ∩ B) = z;
n (A ∪ B) = x + y + z.
Jumlah total elemen = x + y + z + w
Dimana;
X = jumlah elemen yang dimiliki himpunan A.
Y = jumlah elemen yang dimiliki himpunan B.
Z = jumlah elemen yang dimiliki himpunan A dan B keduanya (AB)
W = jumlah elemen yang tidak termasuk dalam himpunan A atau B
Baca juga: Simbol Matematika Lengkap Beserta Artinya – Math Symbol
Cara menggambar diagram Venn
- Himpunan semesta dalam diagram Venn digambarkan sebagai bentuk persegi panjang.
- Setiap himpunan yang sedang dijelaskan digambarkan berupa lingkaran atau kurva tertutup.
- Setiap anggota himpunan masing-masing digambarkan dalam noktah atau titik.
Diagram venn memiliki beberapa bentuk.
Ciri-ciri Diagram Venn
- Himpunan semesta: menggambarkan total data atau nilai yang sedang dibicarakan.
- Daerah yang merupakan himpunan A dan B (A∩B).
- Banyak himpunan anggota A saja (tanpa himpunan B).
- Banyak himpunan anggota B saja (tanpa himpunan A).
- Banyak anggota himpunan semesta, namun bukan bagian dari himpunan anggota A dan himpunan anggota B.
Bentuk Diagram Venn
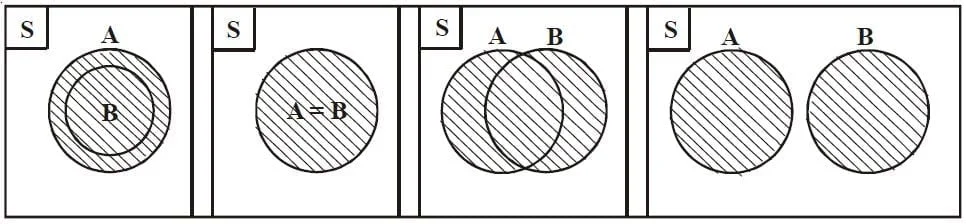
1. Himpunan saling berpotongan
Diagram venn ini digambarkan dimana dua himpunan yang saling berpotongan karena mempunyai kesamaan. Contohnya jika terdapat himpunan A dan B, keduanya saling berpotongan apabila mempunyai kesamaan maka hal ini berarti anggota yang masuk ke dalam himpunan A termasuk juga ke dalam himpunan B.
Himpunan A berpotongan dengan himpunan B dapat ditulis A∩B.
2. Himpunan saling lepas
Himpunan A dan B bisa dikatakan saling lepas jika anggota himpunan A tidak ada yang sama dengan anggota himpunan B. himpunan yang saling lepas ini dapat ditulis A//B.
Himpunan A dapat dikatakan bagian dari himpunan B apabila semua anggota himpunan A merupakan anggota dari himpunan B.
4. Himpunan yang sama
Diagram venn ini menyatakan bahwa jika himpunan A dan B terdiri dari anggota himpunan yang sama, maka dapat kita simpulkan bahwa setiap anggota B merupakan anggota A. contoh A = {2,3,4} dan B= {4,3,2} merupakan himpunan yang sama maka kita dapat menulisnya A=B.
5. Himpunan yang ekuivalen
Himpunan A dan B dikatakan ekuivalen apabila banyaknya anggota dari kedua himpunan sama. Himpunan A ekuivalen dengan himpunan B dapat ditulis n(A)= n(B).
Dalam diagram venn terdapat empat hubungan antarhimpunan meliputi irisan, gabungan, komplemen himpunan dan selisih himpunan.
Irisan
Irisan himpunan A dan B (A∩B) adalah himpunan yang anggota-anggotanya ada didalam himpunan A dan himpunan B.
Sebagai contoh himpunan A ={ 0,1,2,3,4,5} dan himpunan B ={3,4,5,6,7}. perhatikanlah bahwa pada kedua himpunan tersebut terdapat dua anggota yang sama yaitu 3,4 dan 5. Nah, dari kesamaan inilah bisa dikatakan bahwa irisan himpunan A dan B atau di tulis sebagai (A∩B) = {3,4,5}.
Gabungan
Gabungan himpunan A dan B (ditulis A ∪ B) adalah himpunan yang anggota-anggotanya merupakan himpunan A atau anggota himpunan B atau anggota kedua-duanya. Gabungan himpunan A dan B dinotasikan dengan A ∪ B = {x | x ∈ A atau x ∈ B}
Sebagai contoh himpunan A = {1,3,5,7,9,11} dan B= {2,3,5,7,11,13}. Jika himpunan A dan himpunan B digabungkan maka akan terbentuk himpunan baru yang anggotanya dapat di tulis A ∪ B ={1,2,3,5,7,9,11,13}.
Baca juga ? Algoritme Beserta Contoh Soal dan Jawaban
Komplemen
Komplemen himpunan A (ditulis Ac) adalah himpunan yang anggota-anggotanya merupakan anggota himpunan semesta namun bukan anggota himpunan A.
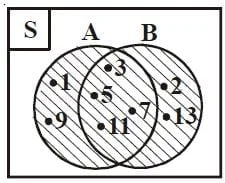
Sebagai contoh S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dan A = {1, 3, 5, 7, 9}. Dapat kita perhatikan bahwa semua anggota S yang bukan dari anggota A membentuk himpunan baru yaitu {0,2,4,6,8}. Maka komplemen dari himpunan A adalah Ac = {0,2,4,6,8}.
Baca juga: Teori Peluang Matematika, Permutasi, Rumus, Ruang Peluang, Contoh Soal dan Jawaban
Soal dan Jawaban Diagram Venn
1. Jika diketahui sebuah P = { h, e, l, l, o }. Berapa banyaknya himpunan dari bagian P?
Jawaban:
Banyaknya anggota dari P yakni n( P ) = 5
Banyaknya himpunan dari bagian P bisa diketahui dengan menggunakan rumus seperti di bawah ini :
2n( P )
Maka caranya ialah seperti ini :
= 2n( P )
= 25
= 32
jadi, hasil banyaknya himpunan dari bagian P tadi ialah = 32.
Dalam survei terhadap 500 mahasiswa di sebuah perguruan tinggi, ditemukan bahwa 49% suka menonton sepak bola (football), 53% suka menonton hoki (hockey), dan 62% suka menonton bola basket (basketball). Juga, 27% suka menonton sepak bola dan hoki keduanya, 29% suka menonton bola basket dan hoki, dan 28% suka menonton sepak bola dan bola basket. 5% tidak suka menonton game ini. Pertanyaan:
Berapa banyak siswa yang suka menonton ketiga pertandingan tersebut?
Temukan rasio jumlah siswa yang hanya suka menonton sepak bola dengan mereka yang hanya suka menonton hoki.
Temukan jumlah siswa yang suka menonton hanya satu dari tiga permainan yang diberikan.
Temukan jumlah siswa yang suka menonton setidaknya dua permainan yang diberikan.
Jawaban:
n (F: football) = persentase siswa yang suka menonton sepak bola = 49%
n (H: hockey) = persentase siswa yang suka menonton hoki = 53%
n (B: basketball) = persentase siswa yang suka menonton bola basket = 62%
n (F ∩ H) = 27%; n (B ∩ H) = 29%; n (F ∩ B) = 28%
Karena 5% suka menonton tidak ada game yang diberikan, maka n (F ∪ H ∪ B) = 95%.
Sekarang menerapkan dengan rumus dasar,
95% = 49% + 53% + 62% -27% – 29% – 28% + n (F ∩ H ∩ B)
Pemecahan, Anda mendapatkan n (F ∩ H ∩ B) = 15%.
Sekarang, buat diagram Venn sesuai informasi yang diberikan.
Catatan: Semua nilai dalam diagram Venn dalam persentase.

Jumlah siswa yang suka menonton ketiga game tersebut = 15% dari 500 = 75.
Rasio jumlah siswa yang hanya menyukai sepak bola dengan yang hanya menyukai hoki = (9% dari 500) / (12% dari 500) = 9/12 = 3: 4.
Jumlah siswa yang suka menonton hanya satu dari tiga permainan yang diberikan = (9% + 12% + 20%) dari 500 = 205
Jumlah siswa yang suka menonton minimal dua game yang diberikan = (jumlah siswa yang suka menonton hanya dua game) + (jumlah siswa yang suka menonton ketiga game tersebut) = (12 + 13 + 14 + 15 )% yaitu 54% dari 500 = 270.
Dari 40 orang bayi, diketahui bahwa ada 18 orang bayi yang suka memakan pisang, lalu ada juga 25 bayi yang suka makan bubur, dan ada pula 9 orang bayi yang menyukai keduanya. Maka hitunglah berapa banyak bayi yang tidak menyukai pisang dan bubur?
Jawaban:
n { A Λ B } = ( n { A } + n { B } ) – ( n { S } – n { X } )
9 = ( 18 + 25 ) – ( 40 – n { X } )
9 = 43 – 40 + n { X }
9 = 3 + n { X }
9 – 3 = n { X }
n { X } = 6 orang bayi
Jadi, banyak bayi yang tidak menyukai pisang dan bubur ada = 6 orang bayi.
Jika diketahui: A = { x | 1 < x 5, maka x ialah bilangan bulat }. B = { x | x 5, maka x ialah bilangan prima }. Berapa hasil dari A ∪ B?
Jawaban nya :
A = { 2, 3, 4 ,5 }.
B = { 2, 3, 5, 7, 11, 13 }.
Simbol dari ( union atau gabungan ) yang artinya ialah salah satu cara untuk menggabungkan anggota himpunan yang saling terkait.
A ∪ B = { 2, 3, 4, 5, 7, 11, 13 }.
Jadi, hasil dari A ∪ B ialah = { 2, 3, 4, 5, 7, 11, 13 }.
Dari 40 orang anggota dari karang taruna, terdapat 21 orang yang gemar bermain tenis meja, lalu ada juga 27 orang yang gemar bermian bulutangkis, dan ada juga 15 orang yang gemar bermain tenis meja dan bulutangkis. Maka hitunglah berapa banyak anggota karang taruna yang tidak gemar bermain tenis meja maupun bulutangkis?
Jawaban:
Misalkan banyak anggota yang tidak menyukai keduanya kita asumsikan dengan huruf x.
- Anggota dari karang taruna berjumlah 40 orang.
- Banyak anggota yang gemar bermain tenis meja dan bulutangkis ada 15 orang.
- Banyak anggota yang gemar bermain bulu tangkis ada 27 – 15 = 12 orang.
- Banyak anggota yang gemar bermain tenis meja ada 21 – 15 = 6 orang.
Maka himpunan tersebut dapat digambarkan dengan bentuk diagram venn seperti gambar yang di bawah ini:
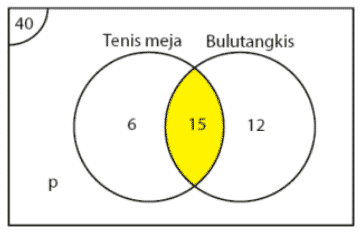
Banyak anggota yang tidak menyukai keduanya ialah:
12 + 15 + 6 + x = 40
33 + x = 40
x = 40 – 33
x = 7 orang anggota
Jadi, banyak anggota karang taruna yang tidak gemar bermain tenis meja maupun bulutangkis ialah sebanyak = 7 orang anggota.
Di ketahui: K = { x | 5 x 9, maka x ialah bilangan asli }. L = { x | 7 x 13, maka x ialah bilangan cacah }. Maka tentukanlah hasil dari K ∪ L ?
Jawaban:
K = { 5, 6, 7, 8, 9 }
L = { 7, 8, 9, 10, 11, 12, 13 }
Simbol ( union atau gabungan ) yang artinya ialah salah satu cara untuk menggabungkan anggota himpunan yang saling terkait.
K ∪ L = { 5, 6, 7, 8, 9, 10, 11, 12, 13 }
Jadi, hasil dari K ∪ L ialah = { 5, 6, 7, 8, 9, 10, 11, 12, 13 }.
Ada 40 orang peserta yang ingin mengikuti sebuah lomba. Lombanya ialah ada baca puisi yang di ikuti oleh 23 orang peserta, lalu ada lagi lomba baca puisi dan menulis cerpen yang di ikuti oleh 12 orang peserta. Maka hitunglah berapa banyak peserta yang mengikuti lomba menulis cerpen?
Jawaban:
Misalkan ada banyak peserta yang tidak mengikuti lomba menulis cerpen di tandai dengan huruf x.
Banyak peserta yang hanya mengikuti lomba puisi ialah sebanyak 23 – 12 = 11 orang peserta.
Di ketahui: A = { x | 1 < x < 20, maka x ialah bilangan prima }. B = { y | 1 y 10, maka y ialah bilangan ganjil }. Maka tentukanlah hasil dari A ∩ B ?
Jawaban nya :
A = { 2, 3, 5, 7, 11, 13, 16, 17, 19 }
B = { 1, 3, 5, 7, 9 }
Simbol yang artinya irisan ialah salah satu cara untuk himpunan anggota yang sama dari himpunan yang saling terkait.
A ∩ B = { 3, 5, 7 }
Jadi, hasil dari A ∩ B ialah = { 3, 5, 7 }.
Dari 42 kambing yang ada di kandang milik pak Johny, ada 30 kambing yang menyukai rumput gajah, dan pula 28 ekor kambing yang menyukai rumput teki. Apabila ada 4 ekor kambing yang tidak menyukai kedua rumput tersebut, maka tentukanlah berapa ekor kambing yang menyukai rumput gajah dan rumput teki tersebut?
Jawaban:
Untuk mencarinya hasil nya, kita akan gunakan rumus himpunan berikut ini:
n { A Λ B } = ( n { A } + n { B } ) – ( n { S } – n { X } )
n { A Λ B } = ( 30 + 28 ) – ( 42 – 4 )
n { A Λ B } = 58 – 38
n { A Λ B } = 20 ekor
Jadi, jumlah kambing yang menyukai kedua jenis rumput tersebut ialah = 20 ekor.
Di sebuah perguruan tinggi, 200 siswa dipilih secara acak. 140 suka teh, 120 suka kopi, dan 80 suka teh dan kopi.
Pertanyaan:
Berapa banyak siswa yang hanya menyukai teh?
Berapa banyak siswa yang hanya menyukai kopi?
Berapa banyak siswa yang tidak menyukai teh atau kopi?
Berapa banyak siswa yang hanya menyukai satu teh atau kopi?
Berapa banyak siswa yang menyukai setidaknya satu minuman?
Solusi: Informasi yang diberikan dapat diwakili oleh diagram Venn berikut, di mana Tea = teh dan Coffee = kopi.

Jeawaban:
Jumlah siswa yang hanya suka teh = 60
Jumlah siswa yang hanya suka kopi = 40
Jumlah siswa yang tidak suka teh atau kopi = 20
Jumlah siswa yang hanya menyukai satu teh atau kopi = 60 + 40 = 100
Jumlah siswa yang menyukai setidaknya satu teh atau kopi = n (hanya Teh) + n (hanya kopi) + n (Teh & kopi) = 60 + 40 + 80 = 180
Bacaan Lainnya
- Rumus Trigonometri Dan Contoh-Contoh Soal Beserta Jawabannya
- Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
- Perasaan Remaja – Apa yang Anda rasakan?
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Pada Daerah Kewanitaan Akibat Pembalut Wanita
- Apakah Produk Pembalut Wanita Aman?
- 10 Cara Menjadi Lebih Pintar Dengan Cepat Dan Menaikan IQ & Terbukti Secara Ilmiah
- Tes Matematika Deret Angka – Hanya Untuk Yang Jenius: Jika 8 = 56, 7 = 42, 6 = 30, 5 = 20, Jadi 3 = ?
- Tes Matematika Deret Angka: Bersama Cara Menghitung Kuadrat Dan Akar Kuadrat
- 10 Cara Dan Strategi Melawan Stres Yang Efektif & Terbukti Secara Ilmiah
- Fungsi, Perbedaan, Cara Berpikir Otak Kiri Dan Kanan
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Hit Bullseye, Wolfram Math World, Investopedia,
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

Bagus artikelnya! terima kasih.