Pangkat Matematika
Berikut adalah tabel “Pangkat Matematika: 2, 3, Akar Kuadrat, Akar Pangkat 2 dan 3” dari 1-100.
| Angka x | Pangkat Dua x2 | Pangkat Tiga (Kubik) x3 | Akar Pangkat Dua x1/2 | Akar Pangkat Tiga (Kubik) x1/3 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1.000 | 1.000 |
| 2 | 4 | 8 | 1.414 | 1.260 |
| 3 | 9 | 27 | 1.732 | 1.442 |
| 4 | 16 | 64 | 2.000 | 1.587 |
| 5 | 25 | 125 | 2.236 | 1.710 |
| 6 | 36 | 216 | 2.449 | 1.817 |
| 7 | 49 | 343 | 2.646 | 1.913 |
| 8 | 64 | 512 | 2.828 | 2.000 |
| 9 | 81 | 729 | 3.000 | 2.080 |
| 10 | 100 | 1000 | 3.162 | 2.154 |
| 11 | 121 | 1331 | 3.317 | 2.224 |
| 12 | 144 | 1728 | 3.464 | 2.289 |
| 13 | 169 | 2197 | 3.606 | 2.351 |
| 14 | 196 | 2744 | 3.742 | 2.410 |
| 15 | 225 | 3375 | 3.873 | 2.466 |
| 16 | 256 | 4096 | 4.000 | 2.520 |
| 17 | 289 | 4913 | 4.123 | 2.571 |
| 18 | 324 | 5832 | 4.243 | 2.621 |
| 19 | 361 | 6859 | 4.359 | 2.668 |
| 20 | 400 | 8000 | 4.472 | 2.714 |
| 21 | 441 | 9261 | 4.583 | 2.759 |
| 22 | 484 | 10648 | 4.690 | 2.802 |
| 23 | 529 | 12167 | 4.796 | 2.844 |
| 24 | 576 | 13824 | 4.899 | 2.884 |
| 25 | 625 | 15625 | 5.000 | 2.924 |
| 26 | 676 | 17576 | 5.099 | 2.962 |
| 27 | 729 | 19683 | 5.196 | 3.000 |
| 28 | 784 | 21952 | 5.292 | 3.037 |
| 29 | 841 | 24389 | 5.385 | 3.072 |
| 30 | 900 | 27000 | 5.477 | 3.107 |
| 31 | 961 | 29791 | 5.568 | 3.141 |
| 32 | 1024 | 32768 | 5.657 | 3.175 |
| 33 | 1089 | 35937 | 5.745 | 3.208 |
| 34 | 1156 | 39304 | 5.831 | 3.240 |
| 35 | 1225 | 42875 | 5.916 | 3.271 |
| 36 | 1296 | 46656 | 6.000 | 3.302 |
| 37 | 1369 | 50653 | 6.083 | 3.332 |
| 38 | 1444 | 54872 | 6.164 | 3.362 |
| 39 | 1521 | 59319 | 6.245 | 3.391 |
| 40 | 1600 | 64000 | 6.325 | 3.420 |
| 41 | 1681 | 68921 | 6.403 | 3.448 |
| 42 | 1764 | 74088 | 6.481 | 3.476 |
| 43 | 1849 | 79507 | 6.557 | 3.503 |
| 44 | 1936 | 85184 | 6.633 | 3.530 |
| 45 | 2025 | 91125 | 6.708 | 3.557 |
| 46 | 2116 | 97336 | 6.782 | 3.583 |
| 47 | 2209 | 103823 | 6.856 | 3.609 |
| 48 | 2304 | 110592 | 6.928 | 3.634 |
| 49 | 2401 | 117649 | 7.000 | 3.659 |
| 50 | 2500 | 125000 | 7.071 | 3.684 |
| 51 | 2601 | 132651 | 7.141 | 3.708 |
| 52 | 2704 | 140608 | 7.211 | 3.733 |
| 53 | 2809 | 148877 | 7.280 | 3.756 |
| 54 | 2916 | 157464 | 7.348 | 3.780 |
| 55 | 3025 | 166375 | 7.416 | 3.803 |
| 56 | 3136 | 175616 | 7.483 | 3.826 |
| 57 | 3249 | 185193 | 7.550 | 3.849 |
| 58 | 3364 | 195112 | 7.616 | 3.871 |
| 59 | 3481 | 205379 | 7.681 | 3.893 |
| 60 | 3600 | 216000 | 7.746 | 3.915 |
| 61 | 3721 | 226981 | 7.810 | 3.936 |
| 62 | 3844 | 238328 | 7.874 | 3.958 |
| 63 | 3969 | 250047 | 7.937 | 3.979 |
| 64 | 4096 | 262144 | 8.000 | 4.000 |
| 65 | 4225 | 274625 | 8.062 | 4.021 |
| 66 | 4356 | 287496 | 8.124 | 4.041 |
| 67 | 4489 | 300763 | 8.185 | 4.062 |
| 68 | 4624 | 314432 | 8.246 | 4.082 |
| 69 | 4761 | 328509 | 8.307 | 4.102 |
| 70 | 4900 | 343000 | 8.367 | 4.121 |
| 71 | 5041 | 357911 | 8.426 | 4.141 |
| 72 | 5184 | 373248 | 8.485 | 4.160 |
| 73 | 5329 | 389017 | 8.544 | 4.179 |
| 74 | 5476 | 405224 | 8.602 | 4.198 |
| 75 | 5625 | 421875 | 8.660 | 4.217 |
| 76 | 5776 | 438976 | 8.718 | 4.236 |
| 77 | 5929 | 456533 | 8.775 | 4.254 |
| 78 | 6084 | 474552 | 8.832 | 4.273 |
| 79 | 6241 | 493039 | 8.888 | 4.291 |
| 80 | 6400 | 512000 | 8.944 | 4.309 |
| 81 | 6561 | 531441 | 9.000 | 4.327 |
| 82 | 6724 | 551368 | 9.055 | 4.344 |
| 83 | 6889 | 571787 | 9.110 | 4.362 |
| 84 | 7056 | 592704 | 9.165 | 4.380 |
| 85 | 7225 | 614125 | 9.220 | 4.397 |
| 86 | 7396 | 636056 | 9.274 | 4.414 |
| 87 | 7569 | 658503 | 9.327 | 4.431 |
| 88 | 7744 | 681472 | 9.381 | 4.448 |
| 89 | 7921 | 704969 | 9.434 | 4.465 |
| 90 | 8100 | 729000 | 9.487 | 4.481 |
| 91 | 8281 | 753571 | 9.539 | 4.498 |
| 92 | 8464 | 778688 | 9.592 | 4.514 |
| 93 | 8649 | 804357 | 9.644 | 4.531 |
| 94 | 8836 | 830584 | 9.695 | 4.547 |
| 95 | 9025 | 857375 | 9.747 | 4.563 |
| 96 | 9216 | 884736 | 9.798 | 4.579 |
| 97 | 9409 | 912673 | 9.849 | 4.595 |
| 98 | 9604 | 941192 | 9.899 | 4.610 |
| 99 | 9801 | 970299 | 9.950 | 4.626 |
| 100 | 10000 | 1000000 | 10.000 | 4.642 |
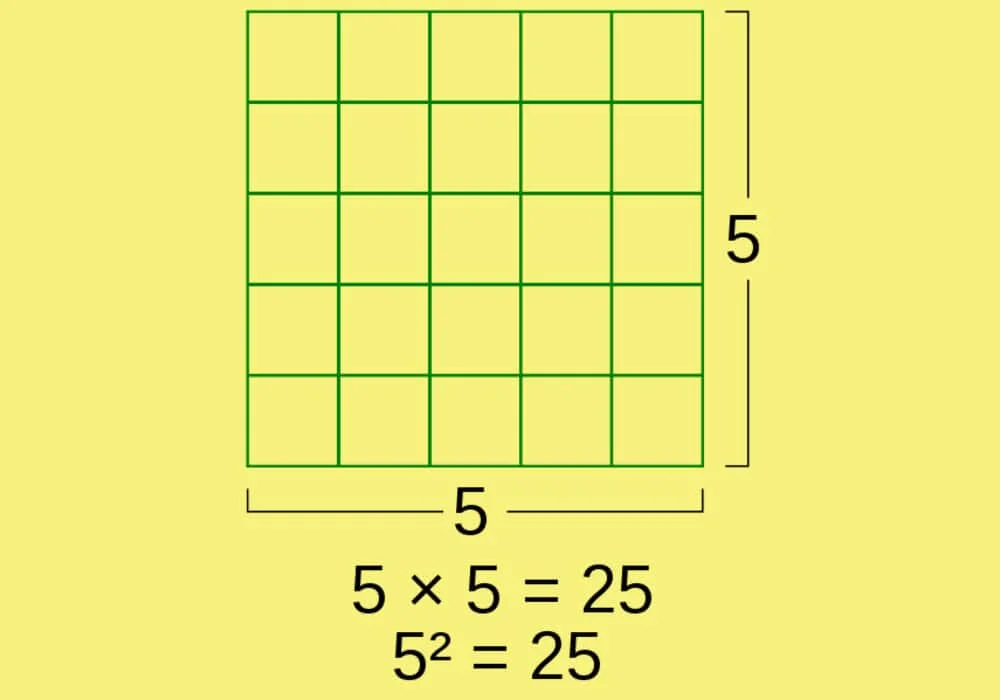
Pangkat 2
Pangkat dua atau bilangan kuadrat (bahasa Inggris: square) dalam matematika adalah hasil perkalian antara suatu bilangan dengan bilangan itu sendiri. Kata kerja “memangkatkan dua” atau “mengkuadratkan” merujuk kepada operasi ini. Dalam pelaksanaannya sama engan memangkatkan dengan bilangan 2, dan dilambangkan dengan angka 2 dalam posisi superskrip. Misalnya kuadrat dari 3 dapat ditulis 32, yaitu sama dengan bilangan 9. Dalam sejumlah kasus di mana penayangan superskrip tidak dimungkinkan, misalnya pada dokumen bahasa pemrograman atau teks biasa, notasi x^2 atau x**2 dapat digunakan untuk menggantikan x2.
Hasil pangkat dua suatu integer dapat juga disebut “bilangan kuadrat” atau “kuadrat sempurna”. Dalam aljabar, operasi pengkuadratan seringkali digeneralisasi ke polinomial, ekspresi lain, atau nilai-nilai dalam sistem matematika yang tidak menyertakan angka. Misalnya, pangkat dua dari fungsi linearx + 1 adalah polinomial kuadrat x2 + 2x + 1.
Salah satu sifat penting dari kuadrat, bagi semua bilangan maupun sistem matematika, adalah bahwa untuk setiap bilangan atau variabel x), pangkat dua dari x adalah sama hasilnya dengan pangkat dua invers aditifnya −x. Jadi fungsi kuadrat memenuhi persamaan x2 = (−x)2. Karenanya fungsi kuadrat merupakan suatu fungsi genap.
Pangkat 3
Pangkat tiga atau bilangan kubik dalam matematika (aritmetika dan aljabar) adalah hasil perkalian suatu bilangan n dua kali berturut-turut dengan dirinya sendiri, atau dikatakan mengalami pemangkatan tiga kali:
- n3 = n × n × n.
Juga merupakan hasil perkalian suatu bilangan dengan hasil kuadratnya:
- n3 = n × n2.
Ini juga merupakan rumus volume untuk kubus secara geometri di mana panjang sisinya adalah n, karena itu operasi ini disebut “kubik”. Fungsi invers operasi ini bertujuan menemukan bilangan yang hasil pangkat tiganya adalah n dengan cara mengekstraksi akar pangkat tiga bilangan n itu. Ini digunakan untuk menghitung panjang sisi suatu kubus yang diketahui volumenya, yang juga merupakan pemangkatan ndengan bilangan sepertiga.
Baik pangkat tiga dan akar pangkat tiga merupakan fungsi ganjil:
- (−n)3 = −(n3).
Pemangkatan tiga dari suatu bilangan atau ekspresi matematika lain dilambangkan dengan suatu superskrip 3, misalnya 23 = 8 atau (x + 1)3.
Fungsi kubik
Dalam matematika, sebuah fungsi kubik atau lebih dikenal sebagai fungsi pangkat tiga adalah suatu fungsi yang memiliki bentuk
dengan a bernilai tidak nol; atau dengan kata lain merupakan suatu polinomial orde tiga. Turunan dari suatu fungsi kubik adalah suatu fungsi kuadrat. Integral dari suatu fungsi kubik adalah fungsi pangkat empat (kuartik).
Menetapkan ƒ(x) = 0 menghasilkan persamaan kubik dengan bentuk:
Biasanya, koefisien a, b, c, dan d merupakan bilangan riil. Untuk menyelesaikan persamaan kubik, caranya dengan mencari akar (nilai nol) dari fungsi kubik.
Titik puncak dan titik belok kubik
Titik puncak suatu fungsi adalah ketika gradien atau turunan pertama fungsi itu sama dengan nol. Titik puncak fungsi kubik:
adalah fungsi kuadrat:
sedangkan titik beloknya diberikan rumus:

Contoh Soal Pangkat Matematika
1. Contoh soal 5 digit : akar pangkat 3 dari 39.304
- 3 digit terakhir 304, nilai satuan nya adalah 4. bilangan pangkat 3 dengan hasil satuan nya 4 adalah 4^3 = 64. jadi jawaban untuk satuan kita dapatkan angka 4
- setelah di ambil 3 digit tersisa angka 39.
- hasil pangkat 3 yang mendekati angka 39 adalah 3^3 = 27. jika kita ambil 4^3 = 64 terlalu besar.
- maka kita dapatkan hasil angka 3 sebagai puluhan
- maka hasil yang di dapatkan dari akar pangkat 3 dari 39.304 adalah 34
- lakukan pengecekan 34 x34 x 34 = 39.304
2. Contoh soal 6 digit : akar pangkat 3 dari 941.192
Penyelesaian :
- 3 digit terakhir 192, nilai satuannya adalah 2. bilangan pangkat 3 yang hasil satuannya 2 adalah 8^3=512
- sehingga kita dapatkan jawaban untuk satuannya adalah 8
- setelah di ambil 3 digit masih tersisa angka 941
- hasil pangkat 3 yang mendekati angka 941 adalah 9^3= 729. jika 10^3 = 1000 terlalu besar
- sehingga di dapat jawaban untuk nilai puluhannya adalah 9
- maka hasil yang di dapatkan dari akar pangkat 3 dari 941.192 adalah 98
- lakukan pengecekan 98 x 98 x 98 = 941.192
3. Kerjakan akar pangkat dibawah ini:
Langkah pertama memahami cara cepat ini adalah dengan menghafal pola ujung bilangan pangkat tiga. Perhatikan bilangan pangkat tiga berikut !
1 x 1 x 1 = 1 → ∛1 = `1
2 x2 x 2 = 8 → ∛8 = 2
3 x 3 x 3 = 27 → ∛27 = 3
4 x 4 x 4 = 64 → ∛64 = 4
5 x 5 x 5 = 125 → ∛125 = 5
6 x 6 x 6 = 216 → ∛216= 6
7 x 7 x 7 = 343 → ∛343= 7
8 x 8 x 8 = 512 → ∛512= 8
9 x 9 x 9 = 729 → ∛729= 9
10 x10 x10 = 1000 → ∛1000 = 10
4. Hasil dari 5³ adalah?
Jawaban:
5 x 5 x 5
5. Sebuah kubus mempunyai rusuk 15 cm. Volumenya…
Jawaban:
153 = 3375
5. Hasil dari  :
:
Jawaban:
9x9x9= 729
dikurangi
2x2x2 = 8
ditambah
5x5x5 = 125
sama dengan
846
6. Jawaban dari ∛1.331 =
Jawaban:
11 → ujungnya 1 hasilnya 1, angka depannya 1 hasilnya 1 (karena kurang dari batas 8), jawabannya 11
7. Hasil dari 25³ x 2³ =
Jawaban:
25x25x25 = 15 625
dikali
2x2x2 = 8
sama dengan
125 000
8. Hasil dari ∛2.744 =
Jawaban:
14 → ujungnya 4 hasilnya 4, angka depannya 2 hasilnya 1 (karena 2 kurang dari 8), jawabannya 14
9. Selesaikan soal dibawah ini
52 =
12 =
102 =
√100
Jawaban:
- 52 = 25
- 12 = 1
- 102 = 100
- √100 = 10
10. Hasil dari dari ∛21.952 =
Jawaban:
28 → ujungnya 2 hasilnya 8, angka depannya 21 hasilnya 2 (karena 21 kurang dari 27), jawabannya 28
11. Bagaimana dengan akar pangkat tiga yang lebih kompleks ∛571.787 =
Jawaban:
83 → ujungnya 7 hasilnya 3, angka depannya 571 hasilnya 8 (karena 571 kurang dari 729), jawabannya 83.
12. Selesaikan x3 – 7x2 + 4x + 12 = 0
Jawaban:
f(x) = x3 – 7x2 + 4x + 12
Nilai yang mungkin adalah ±1, ±2, ±3, ±4, ±6, ±12
Kita mendapatkan f(–1) = –1 – 7 – 4 + 12 = 0
Jadi, (x + 1) adalah faktor dari f(x)
x3 – 7x2 + 4x + 12
= (x + 1)(x2 – 8x + 12)
= (x + 1)(x – 2)(x – 6)
Jadi, akarnya –1, 2, 6
13. Berapa 7,1 × 10-3?
Maka, operasi kebalikannya 7,1 x (1/10 × 1/10 × 1/10) = 7,1 x 0,001 = 0,0071
14. Hasil dari 5 × 10-3 =
Jawaban:
5 ÷ 10 ÷ 10 ÷ 10 = 0,005
15. Berapa 1,35 × 104 ?
Perhitungan dapat dibuat sebagai berikut: 1,35 x (10 × 10 × 10 × 10) = 1,35 x 10.000 = 13.500
16. Sederhanakan hasil perkalian bilangan berpangkat berikut ini, kemudian tentukan nilainya
7² × 7⁵
(–2)⁴ × (–2)⁵
(–3)³ × (–3)7
2³ × 3⁴
3y² × y³
2x4 × 3x6
–2² × 2³
–27 × 28
–35 × 35
Penyelesaian
- 7² × 7⁵ = 72+5 = 77 = 823.543
- (–2)⁴ × (–2)⁵ = –22+5 = –29 = – 512
- (–3)³ × (–3)7 = –33+7 = –310 = 59.049
- 2³ × 3⁴ , soal ini tidak sanggup disederhanakan lantaran bilangan pokonya berbeda (2 dan 3). Makara kita hanya sanggup menghitung nilainya saja. 2³ × 3⁴ = 8 × 81 = 648
- 3y² × y³= 3(y)2+3 = 3y5
- 2x4 × 3x6= (2×3)(x)34+6 = 6x10
- –2² × 2³ = (–1)² × 2² × 2³ = (1) × 22+3 = 25 = 32
- –27 × 28 = (–1)7 × 27 × 28 = (–1) × 27+8 = –(215) = – 32.768
- –35 × 35= (–1)5 × 35 × 35 = (–1) × 36+6 = –(312) = – 531.441
17. Sederhanakan hasil perpangkatan bilangan berpangkat berikut ini, kemudian tentukan nilainya
- (2/3)²
- [(−3)/2]³
- [6/(−5)]²
- [(1/2)/(1/3)]³
- (−2p/q)³
- (x/(−3)y)⁴
- (2/3)² = 2²/5² = 4/25
- [(−3)/2]³ = (−3)³/2³ = −27/8
- [6/(−5)]² = 6²/(−5)² = 36/25
- [(1/2)/(1/3)]³ = (1/2)³/(1/3)³ = (1/8)/(1/27) = 27/8
- (−2p/q)³ = [(−2)³ × (p)³]/q³ = −8p³/q³
- (x/(−3)y)⁴ = x⁴/[(−3)⁴ × (y)⁴]=x⁴/81y⁴
Bacaan Lainnya
- Tes Matematika Deret Angka: Jika 2+3=13, 3+4=25, 4+5=41, Jadi 5+6=??
- Penjelasan Akar Kuadrat / Pangkat
- Pangkat Eksponen- Integer – Daftar eksponensial bilangan bulat dan contoh soal dan jawaban
- Makanan Penambah Sel Darah Merah – Penguat Sistem Imun
- Kromosom Manusia – Bioinformatika Cabang Biologi
- Fungsi, Jenis – Penyakit Sumsum Tulang
- Gagal Ginjal – Penyakit Ginjal Kronik -Tanda, Gejala, Penyebab, Perawatan, Pencegahan, Diteksi Dini
- Makanan Penurun Darah Tinggi – Terbukti Secara Sains
- Leukemia Adalah Kanker Darah – Apakah Saya Beresiko? Apa Yang Anda Ketahui Tentang Kanker Ini?
- Berapa Banyak Rata-Rata Sel Kulit Manusia Hilang Dalam Hidupnya?
- Sebagian cabang biologi: Biofisika
- Kanker Payudara – Diteksi Dini, Cegah Dan Pemeriksaan Ditanggung Pemerintah
- Kanker Serviks / Leher Rahim Wanita – Diteksi Dini, Cegah Dan Pemeriksaan Ditanggung Pemerintah
- Kenapa cabai memberi sensasi pedas & panas? Dapat juga mencegah beberapa jenis kanker!
- Apakah Matahari Berputar Mengelilingi Pada Dirinya Sendiri?
- Test IPA: Planet Apa Yang Terdekat Dengan Matahari?
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- TOP 10 Virus Paling Mematikan Manusia
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing