Pecahan (Fraksi)
Pecahan adalah istilah dalam matematika yang terdiri dari pembilang dan penyebut. Hakikat transaksi dalam bilangan pecahan adalah bagaimana cara menyederhanakan pembilang dan penyebut.
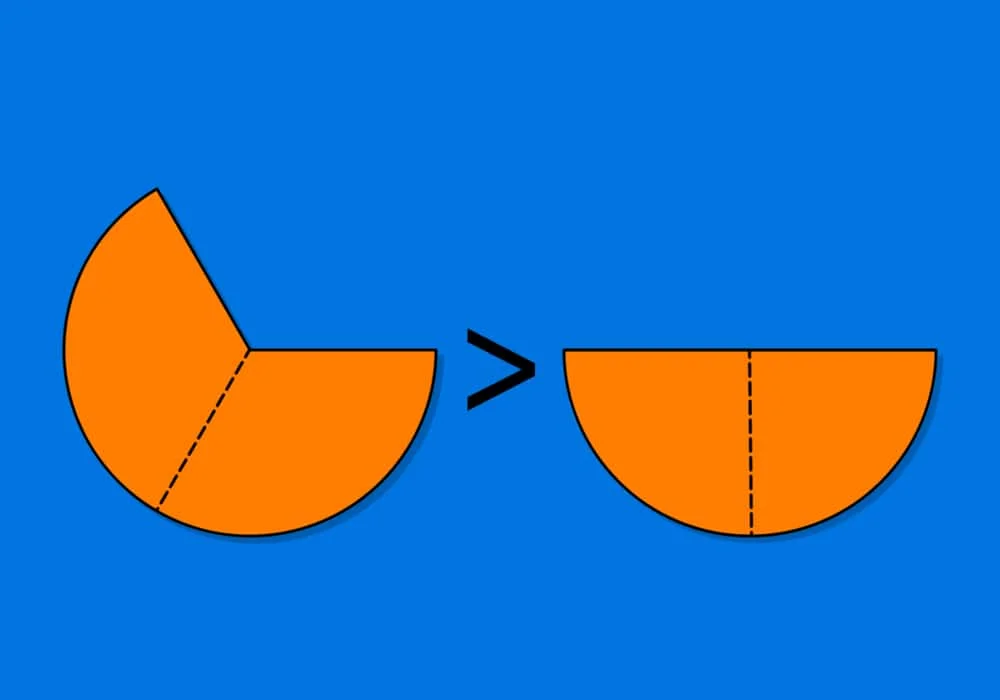
Penyederhanaan pembilang dan penyebut akan memudahkan dalam operasi aritmetika sehingga tidak menghasilkan angka yang terlalu besar tetapi tetap mempunyai nilai yang sama. Contohnya: bila dibandingkan antara 50/100 dan ½ maka lebih mudah dan sederhana melihat angka ½. 50/100 terlihat sebagai ”angka raksasa” yang kelihatannya lebih kompleks dibandingkan ½, padahal sebenarnya kedua angka ini tetap memiliki nilai yang sama.
Pada operasi penjumlahan dan pengurangan pada pecahan selain disederhanakan juga penyebutnya harus disamakan dengan bilangan yang sama, sedangkan pada operasi perkalian caranya adalah pembilang dikali pembilang, penyebut dikali penyebut. dan dalam operasi pembagian, pecahan yang di kanan dibalikkan, setelah dibalikkan, tanda : diubah menjadi tanda kali (X), seperti 3/4 : 5/6 = 3/4 X 6/5 = 18/20 = 9/10.
Macam-macam pecahan
Pecahan merupakan istilah martematika yang terdiri dari pembilang serta penyebut. Ada beberapa macam bilangan pecahan, antara lain sebagai berikut :
1. Biasa
Pecahan biasa merupakan pecahan yang pembilang serta penyebutnya adalah bilangan bulat. Contohnya : 1/2, 3/4, 5/7, 6/8, dan sebagainya.
2. Murni
Suatu pecahan dapat disebut sebagai pecahan murni jika pembilang serta penyebutmya merupakan bilangan bulat dan nilai pembilangnya lebih kecil dari penyebutnya. Contohnya : 1/7, 2/12, 3/18, 4/17, dan sebagainya.
3. Campuran
Pecahan campuran ini merupakan kombinasi dari bagian bilangan bulat dan bagian pecahan murni. Contohnya : 2½, 3¼, 5¾, dan lain sebagainya.
4. Desimal
Pecahan desimal merupakan pecahan yang penyebutnya 10, 100, 1000. dst. Yang selanjutnya dinyatakan dengan tanda koma seperti berikut ini.
3/10 = 0,3
58/100 = 0,58
4700/1000 = 4,7
5. Persen atau Perseratus
Persen merupakan pecahan yang penyebutnya merupakan nilai 100 dan dinyatakan dengan lambang %. Contohnya sebagai berikut.
6% = 6/100
15% = 15/100
74% = 74/100
dan lain sebagainya.
Baca juga: Cara Menghitung Persen Rumus, Contoh Soal, Jawaban, Pengertian, Sejarah
6. Permil atau perseribu
Permil merupakan pecahan yang penyebutnya adalah nilai 1000 dan dinyatakan dengan lambang ‰, contohnya sebagai berikut.
6‰ = 6/1000
9‰ = 9/1000
12‰ = 12/1000
207‰ = 207/1000
dan lain sebagainya
Rumus Operasi Hitung Penjumlahan dan Pengurangan Bilangan Pecahan
Penjumlahan Bilangan Pecahan
Untuk menjumlahkan bilangan pecahan yang memiliki penyebut sama sangatlah mudah. Kalian cukup menjumlahkan angka yang ada di bagian atas atau biasa dinamakan sebagai “pembilang”. Pahami contoh penjumlahan pecahan berikut ini:
1/2 + 3/2 = 4/2
Sedangkan untuk menjumlahkan pecahan yang kedua penyebutnya berbeda maka kalian harus mengubah atau menyamakan penyebutnya terlebih dahulu. Hal ini dikarenakan bilangan pecahan tidak bisa dijumlahkan secara langsung apabila penyebutnya berbeda nilai. Simak contoh berikut:
1/5 + 2/3 = 3/15 + 10/15 = 13/15
Tips:
Pertama ubahlah terlebih dahulu pecahan tersebut agar penyebutnya menjadi sama yaitu dengan menggunakan KPK dari kedua penyebut itu. Seperti pada operasi hitung di atas KPK dari 3 dan 5 adalah 15
Apabila penyebut dikalikan dengan suatu bilangan maka pembilangnya pun harus dikalikan juga.
Tips penjumlahan pada bilangan pecahan campuran
- Pecahan campuran merupakan perpaduan antara bilangan asli dan bilangan campuran.
- Operasi hitung pada bilangan pecahan campuran bisa dilakukan seperti ini:
- Ubahlah dahulu bilangan pecahan campuran menjadi pecahan biasa.
- Kemudian ubah penyebutnya agar sama dengan menggunakan kpk dari kedua penyebut.
- Jumlahkan kedua pecahan.
- Hasilnya kemudian disederhanakan kembali menjadi pecahan campuran.
Pengurangan bilangan pecahan
Konsep pengurangan pada bilangan pecahan biasa sama saja seperti pada penjumlahan. Bila penyebutnya sama tinggal kita kurangkan saja angka yang ada di atas. Contohnya:
9/6 – 2/6 = 7/6
Untuk bilangan pecahan yang penyebutnya berbeda pun sama, kita harus menyamakan penyebutnya dengan mencari kpk dari kedua bilangan penyebut itu. Contohnya:
4/2 – 2/6 = 24/12 – 4/12 = 20/12
Pengurangan bilangan pecahan campuran
Caranya sama saja seperti pada penjumlahan pecahan campuran. Kita harus mengubah pecahan campuran menjadi pecahan biasa terlebih dahulu. Lalu disamakan penyebutnya. Setelah dikurangkan, hasilnya disederhanakan.
Operasi hitung campuran
Cara menghitung pecahan dengan mudah
I – Jumlah dan selisih pecahan
Ketika dua pecahan memiliki penyebut yang sama, maka kita menambah atau mengurangi pembilangnya dan mempertahankan penyebutnya.
Contoh: 15/12 + 14/12 = 29/12 dan 15/12 – 15/12 = 1/12
Ketika dua pecahan tidak memiliki penyebut yang sama, pertama-tama kita membuat mereka memiliki penyebut yang sama dan kemudian menambahkan atau mengurangi pembilangnya.
Contoh:
15/4 + 11/16 = 15×3/4×3 + 11×2/6×2 = 45/12 + 22/12 = 67/12
15/4 – 11/6 = 15×3/4×3 – 11×2/6×2 = 45/12 – 22/12 = 23/12
II – Perkalian dan pembagian
Untuk mengalikan dua pecahan, kalikan penyebutnya dan pembilangnya dikalikan.
Contoh: 5/8×7/12 = 5×7/8×12 = 35/96
Secara khusus, untuk mengalikan pecahan dengan bilangan asli, kita hanya mengalikan pembilangnya dengan angka ini dan penyebutnya tetap.
Contoh: 5/8×3 = 5×3/8 = 15/8
Untuk membagi dua pecahan, kalikan pecahan pertama dengan kebalikan pecahan kedua.
Contoh: 5/8 : 7/2 = 5/8×12/7 = 1×12/8×7 = 5×3/2×7 = 15/14
Contoh Soal dan Jawaban Pecahan
1. Pecahan senilai 2⁄3 dengan…
b. 3⁄6
c. 5⁄15
d. 6⁄9
2. Bentuk paling sederhana dari 75⁄100 adalah….
b. 1⁄2
c. 1⁄4
d. 3⁄4
3. Pecahan di bawah ini yang tidak senilai dengan 1⁄3 adalah…
b. 4⁄6
c. 3⁄9
d. 5⁄15.
4. Pecahan 2⁄5 merupakan bentuk sederhana dari pecahan-pecahan di bawah ini, kecuali ….
b. 8⁄20
c. 10⁄25
d. 20⁄100
5. Bentuk paling sederhana dari 16⁄32 adalah…
b. 1⁄5
c. 1⁄2
d. 1⁄8
Jawaban: c. 1⁄2
6. Urutkanlah pecahan dari yang paling kecil: 20⁄100 , 3⁄6 , 7⁄12 , 2⁄8
Jawaban: 20⁄100 , 2⁄8 , 7⁄21 , 3⁄6
7. Pak John memiliki 15 tabung berisi madu. Setiap tabung berisi 10 liter madu. Kemudian Pak John ingin memasukkan madu tersebut ke dalam botol kecil-kecil untuk dijual. Setiap botol kecil mampu menampungliter madu. Setiap botol nantinya akan dijual dengan harga Rp. 50.000,00. Dari keterangan tersebut. Maka, hitunglah:
a. Jumlah maksimal botol yang bisa digunakan untuk menampung madu, jika diisi peuh setiap botolnya.
b. Jumlah uang yang diterima Pak John jika madunya terjual semua.
Jumlah tabung berisi madu = 15 tabung
Isi setiap tabung = 10 1⁄2 liter madu
Volume botol kecil = 1⁄4 liter madu.
Harga setiap botol kecil madu = Rp. 50.000,00.a. Jumlah maksimal botol yang bisa digunakan untuk menampung madu, jika diisi peuh setiap botolnya.
= 15 x 10 1⁄2 : 1⁄4 = 15 x 21⁄2 x 4⁄1 = 315⁄2 x 4⁄1 = 1260⁄2 = 630 botolb. Jumlah uang yang diterima Pak John jika madunya terjual semua.
= 630 x Rp. 50.000,00 = Rp. 31.500.000,00
8. Bu Tina membuat 20 roti dan 10 kue bolu untuk murid-muridnya. Rotinya dipotong-potong dengan ukuran 1⁄2 bagian dan bolunya dipotong 1⁄4 bagian. Maka jumlah semua potongan roti dan bolu adalah…
b. 30 potongan
c. 40 potongan
d. 50 potongan
9. Urutkanlah pecahan-pecahan di bawah ini dari yang terkecil ke terbesar!
a. 10⁄100 , 2⁄5 , 7⁄20 , 3⁄4 , 3⁄25
b. 1⁄3 , 2⁄9 , 12⁄18 , 2⁄4 , 15⁄36
Jawaban:
Untuk mengurutkan pecahan-pecahan di bawah ini dari yang terkecil, caranya adalah dengan menyamakan penyebutnya terlbih dahulu.
a. 10⁄100 , 2⁄5 , 7⁄20 , 3⁄4 , 3⁄25
10⁄100 x 1⁄1 = 10⁄100
2⁄5 x 20⁄20 = 40⁄100
7⁄20 x 5⁄5 = 35⁄100
3⁄4 x 25⁄25 = 75⁄100
3⁄25 x 4⁄4 = 12⁄100
Jadi urutannya dari yang terkecil adalah 10⁄100 , 3⁄25 , 7⁄20 , 2⁄5 , , 3⁄4
b. 1⁄3 , 2⁄9 , 12⁄18 , 2⁄4 , 15⁄36
1⁄3 x 12⁄12 = 12⁄36
2⁄9 x 4⁄4= 8⁄36
12⁄18 x 2⁄2 = 24⁄36
2⁄4 x 9⁄9= 18⁄36
15⁄36 x 1⁄1= 15⁄36
Jadi urutannya dari yang terkecil adalah 2⁄9 , 1⁄3 , 15⁄36 , 2⁄4 , 12⁄18
10. Ibu Siska mempunyai sawah seluas 1 1⁄2 hektar, kemudian pada tahun 2017 ia membeli lagi sawah seluas 1⁄4 hektar dan 4⁄5 hektar. Sawah Pak Dani tersebut ditanami jagung seluas 3⁄5 bagian, padi seluas 1⁄3 bagian dan 1⁄15 ditanami kacang tanah. Dari keterangan tersebut, maka hitunglah:
a. Luas sawah yang dimiliki Ibu Siska.
b. Luas masing-masing sawah yang ditanami jagung, padi dan kacang tanah.
= 1 1⁄2 hektar + 1⁄4 hektar + 4⁄5 hektar
= 3⁄2 + 1⁄4 + 4⁄5
= 30⁄20 + 5⁄20 + 16⁄20
= 51⁄20
= 2 11⁄20 hektarb. Luas masing-masing sawah yang ditanami jagung, padi dan kacang tanah.
– Luas sawah yang ditanami jagung = 211⁄20 hektar x 3⁄5 = 51⁄20 x 3⁄5 = 153⁄100 = 1 3⁄100 hektar
– Luas sawah yang ditanami padi =2 11⁄20 hektar x= x 1⁄3 = 51⁄20 x 1⁄3 = 51⁄60 = 17⁄20 hektar
– Luas sawah yang ditanami kacang tanah = 2 11⁄20 hektar x 1⁄15= 51⁄20 x 1⁄15 = 51⁄300 = 17⁄100 hektar
11. Hitunglah hasil dari perkalian-perkalian pecahan berikut ini.
a. | 3 | × | 2 | 1 |
8 | 5 |
b. | 5 | 1 | × | 7 | 2 |
2 | 3 |
c. | 4 | 1 | × | 2 | 4 |
6 | 5 |
a. | 3 | × | 2 | 1 | = | 3 | × | 11 | = | 33 |
8 | 5 | 8 | 5 | 40 |
b. | 5 | 1 | × | 7 | 2 | = | 11 | × | 23 | = | 11 × 23 | = | 253 |
2 | 3 | 2 | 3 | 2 × 3 | 6 |
c. | 4 | 1 | × | 2 | 4 | = | 25 | × | 14 | = | 5 × 7 | = | 35 | = | 11 | 2 |
6 | 5 | 6 | 5 | 3 × 1 | 3 | 3 |
12. Hitunglah hasil dari perkalian-perkalian pecahan berikut ini.
a. | 2 | × | 4 |
5 | 7 |
b. | 2 | × | 3 |
9 | 2 |
c. | 5 | × | 7 |
8 | 9 |
a. | 2 | × | 4 | = | 2 × 4 | = | 8 |
5 | 7 | 5 × 7 | 35 |
b. | 2 | × | 3 | = | 2 × 3 | = | 6 | = | 1 |
9 | 2 | 9 × 2 | 18 | 3 |
c. | 5 | × | 7 | = | 5 × 7 | = | 35 |
8 | 9 | 8 × 9 | 72 |
13. Hitunglah hasil dari pembagian antara bilangan bulat dengan pecahan berikut ini.
6 | : | 6 |
9 |
6 | : | 6 | = | 6 | × | 9 | = | 9 |
9 | 6 |
14. Hitunglah hasil dari pembagian pecahan dengan pecahan berikut ini.
a. | 3 | : | 4 |
5 | 15 |
b. | 3 | 2 | : | 2 | 1 |
3 | 3 |
a. | 3 | : | 4 | = | 3 | × | 15 | = | 3 × 3 | = | 9 |
5 | 15 | 5 | 4 | 1 × 4 | 4 |
b. | 3 | 2 | : | 2 | 1 | = | 11 | : | 7 | = | 11 | × | 3 | = | 11 |
3 | 3 | 3 | 3 | 3 | 7 | 7 |
15. Soal Cerita: Hasil kali dua bilangan sama dengan 39. Salah satu bilangan itu bernilai 41/3. Tentukanlah bilangan lainnya!
16. Hitunglah bilangan-bilangan berikut dengan memberikan hasilnya sebagai pecahan sederhana: 2/3 + 5/6:
17. Latihan tentang aturan untuk menghitung pecahan: kami berbagi warisan. Saya mengambil seperempatnya dan saudara laki-laki saya dua pertiga sisanya. Berapa banyak warisan yang diterima saudara saya?
Jawaban:
Setelah 1/4 bagianku, tersisa 3/4 bagian warisan. Tetapi saudara saya mengambil 2/3 sisanya, yaitu 2/3 dari sisa 3/4: kita kalikan.
Jadi bagian saudara laki-laki saya sesuai dengan: 2/3 x 3/4 = 2/4 = 1/2 jadi, itu berarti setengah dari total warisan.
18. Di sebuah perusahaan terdapat 42 eksekutif yang mewakili 6/11 dari karyawan. Berapa banyak karyawan yang ada di perusahaan ini?
Jawaban:
Kami tahu apa yang diwakili 6/11, kami mencari berapa banyak semuanya 11/11 (atau 1).
Kami akan menggunakan aturan tiga: kami kembali ke unit sebelum menghitung apa yang kami inginkan.
Jika 6/11 adalah 42, maka 1/11 adalah 6 kali lebih kecil dari 7 (42÷6).
Jika 1/11 adalah 7, maka 11/11 atau keseluruhannya adalah 77 (11 kali lebih banyak)
Jadi ada 77 karyawan di perusahaan ini.
19. Kotak coklat yang dibeli John berisi 450 gram, dia makan 5/9 darinya. Berapa gram cokelat yang dia makan?
Jawaban:
Jika kotak coklat tersebut dibagi menjadi 9 bagian yang sama dan ia mengambil 5 bagian tersebut. Emas 450÷9 = 50 gram per irisan. Jadi 5 bagian mewakili 250 gram.
Metode lain dengan menerapkan kursus tentang pecahan:
John makan 5/9 dari 450 gram, maka perhitungannya adalah: 5/9 x 450
Dengan menghitung kita mendapatkan: 5/9 x 450=
5×450/9 = 5x9x50/9 = 5 x 50 = 250 gram
20. Berapa setengah dari empat perlima dari lima pertujuh dari 14?
Jawaban:
Ingatlah bahwa “dari” berarti “x” dalam pernyataan pecahan atau persentase
Kita peroleh: (1/2 x 4/5 x5/7) x14 = 1/2 x (2×2/5) x 5/7 x 7 x 2=
2×2 = 4
Jenis Bilangan Matematika: Asli, Prima, Ganjil, Genap, Rasional, Irrasional, Imajiner, Komposit, Kompleks, Romawi…
Klik disini untuk membaca tentang bilangan matematika lainnya. (Akan membuka layar baru, tanpa meninggalkan layar ini).
Bacaan Lainnya
- Cara Mengubah Pecahan Biasa menjadi Desimal
- Cara Mengubah Pecahan Biasa menjadi Perbandingan
- Bagaimana Cara Menjalankan Mobil Dengan Bahan Bakar Jagung?
- Siapa Yang Menemukan Antibiotik? Dia Menyelamatkan Miliaran Nyawa!
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Cara Menulis Cepat & Efektif Dengan Tangan Atau Komputer – Pasti Berhasil
- Fakta Bumi
- Jarak Matahari Ke Bumi Yang Paling Tepat Adalah 149.597.870.700 Meter
- Arti Mimpi ~ Tafsir, Definisi, Penjelasan Mimpi Secara Psikologi
- Organ Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Berciuman: Tips, Nasihat Dan Langkah Untuk Ciuman Pertama Yang Sempurna
- Kepalan Tangan Menandakan Karakter Anda – Kepalan nomer berapa yang Anda miliki?
- 7 Cara Untuk Menguji Apakah Dia, Adalah Teman Sejati Anda Atau Bukan BFF (Best Friend Forever)
- 10 Cara Menjadi Lebih Pintar Dengan Cepat Dan Menaikan IQ – Terbukti Secara Ilmiah
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan Pasti Sukses!
- Fungsi, Perbedaan, Cara Berpikir Otak Kiri Dan Kanan
- 10 Kegiatan Yang Akan Membantu Otak Anda Menjadi Tetap Muda Dan Tajam
Tes Matematika
- Tes Matematika: Deret Angka: 12, 23, 34, 45, ?
- Tes Matematika: Otak Atik Otak – Jumlah nomor yang harus didapatkan: 50 & Nomor yang diberikan: 2 8 9 15 20 40
- Soal Tes Matematika: Berapa Jumlah Total Kubus Putih?
- QUIZ Matematika Deret Aritmatika: jika 11 X 11 = 4, jadi 33 X 33 = ??
- Tes Matematika Logika Aritmatika: Jika 3 + 1 = 24, 5 + 2 = 37, Jadi 7 + 5 = ???
- QUIZ Matematika: Apel, Pisang dan Semangka
- Tes Matematika Deret Angka: Jika 2+3=13, 3+4=25, 4+5=41, Jadi 5+6=??
Unduh / Download Aplikasi HP Pinter Pandai
Respons “ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: CleverlySmart, Davenport University, CueMath, MathIsFun
Sumber foto utama: Ezra M. Katz (CC BY-SA 3.0) via Wikimedia Commons
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

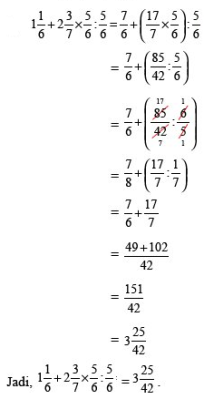
Sangat menyenangkan…………….ingin belajar terus
Apa an sih tuh yg di bacaan lainnya segala pake ada cara berciuman ,,ini kan tentang pelajaran knp sih ngerusak moral anak2 bangsa aja ,,ga jelas banget
Kak itu pertanyaan no 4 yg d 20/100 itu kalo di kecilin paling kecil itu 1/5 bukan 2/5
Terimakasih artikelnya yang berjudul Cara Menghitung Pecahan Matematika Beserta Contoh Soal dan Jawaban di pinterpandai.com ini. Sangat membantu
sangat bermanfaat sekali kak
makasih buat artikelnya kak
nama saya : susi susanti mariana
nim : 1722500114
jurusan : sistem informasi
kunjungi situs website kampus kami ya kak di https://www.atmaluhur.ac.id
Good