Rumus Lingkaran

Berikut rumus lingkaran:

Luas lingkaran: Luas = π r2
Luas setengah lingkaran: L = 1/2 x π x r2
Diameter lingkaran: 2.r
Jari-jari lingkaran: r = K/2 phi
Keliling setengah lingkaran: K = π x r
Keliling lingkaran: Keliling = π x d

Rumus Volume

Kubus: Volume = s3 atau S x S x S
Balok: Volume = Panjang x Lebar x Tinggi
Prisma: Volume = Luas alas x Tinggi
Tabung atau silinder: Volume = pi.r^2.h
Bola: Volume = 4/3 pir³
Kerucut: Volume = 1/3 pir2h
Piramida: Volume = 1/3 x la x h
Limas segitiga:
- Luas alas limas = 1/2 x a x t
- Luas permukaan limas = Luas alas + jumlah luas seluruh sisi tegak
- Volume limas segitiga: V = 1/3 x (1/2 x Panjang x Lebar ) x Tinggi
Rumus Limas Segi Empat Luas: (L) = Luas alas + 4 X Luas sisi
- Yang dimana kita tahu:
  - luas alas limas = sisi×sisi
  - luas sisi tegak segitiga = (½×alas×tinggi)×4
- Volume limas segiempat =1/3 x Panjang x Lebar x Tinggi
  atau
  Volume (V) = 1/3 x Luas Alas x Tinggi

Tabel Rumus Volume

Bentuk	Rumus volume	Variabel
Kubus	$a^{3}\;$	a = panjang sisi/rusuk
Silinder	$\pi r^{2}h\;$	r = jari-jari alas, h = tinggi
Prisma	$B\cdot h$	B = luas alas, h = tinggi
Balok	$l\cdot w\cdot h$	l = panjang, w = lebar, h = tinggi
Prisma segitiga	${\frac {1}{2}}bhl$	b = panjang dasar segitiga, h = tinggi prisma, l = length of prism or distance between the triangular bases
Bola	${\frac {4}{3}}\pi r^{3}$	r = jari-jari bola di mana merupakan integral luas permukaan bola
Ellipsoid	${\frac {4}{3}}\pi abc$	a, b, c = semi-axes of ellipsoid
Torus	$(\pi r^{2})(2\pi R)=2\pi ^{2}Rr^{2}$	r = jari-jari kecil, R = jari-jari besar
Limas	${\frac {1}{3}}Bh$	B = luas alas, h = tinggi limas
Limas persegi	${\frac {1}{3}}s^{2}h\;$	s = sisi samping alas limas, h = tinggi
Limas segiempat	${\frac {1}{3}}lwh$	l = panjang, w = lebar, h = tinggi
Kerucut	${\frac {1}{3}}\pi r^{2}h$	r = jari-jari lingkaran di dasar kerucut, h = jarak dari dasar ke pucuk atau tinggi
Tetrahedron	${{\sqrt {2}} \over 12}a^{3}\,$	panjang sisi $a$
Parallelepiped	${\begin{aligned}K=&1+2\cos(\alpha )\cos(\beta )\cos(\gamma )\\&-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\end{aligned}}$	a, b, and c are the parallelepiped edge lengths, and α, β, and γ are the internal angles between the edges
Volume benda putar (dibutuhkan kalkulus)	$\int _{a}^{b}A(h)\,\mathrm {d} h$	h = dimensi apapun, A(h) = luasan cross-section tegak lurus terhadap h yang didefinisikan sebagai fungsi posisi sepanjang h. a dan b adalah batas integrasi volume putar. (Berlaku untuk semua bangun jika cross-sectional area nya dapat ditentukan dari h).
Semua benda diputar (dibutuhkan kalkulus)	$\pi \int _{a}^{b}\left({\left[R_{O}(x)\right]}^{2}-{\left[R_{I}(x)\right]}^{2}\right)\mathrm {d} x$	$R_{O}$ dan $R_{I}$ menyatakan fungsi dari jari-jari luar dan jari-jari dalam fungsi, secara berurutan.

Test Matematika Lingkaran

Temukan dibawah ini rumus lingkaran dan volume, beserta tes matematika lingkaran!

3 1 4 1 5 ? 2 6 5 3 5 8 ? 7 ? 3
Angka berapa yang menggantikan tanda ?

Apakah Lingkaran?

Lingkaran adalah himpunan semua titik di bidang datar yang berjarak sama dari suatu titik tetap di bidang tersebut.

Titik tetap lingkaran itu dinamakan pusat lingkaran, sedangkan jarak dari suatu titik pada lingkaran ke titik pusat dinamakan jari-jari lingkaran.

Istilah-Istilah Dalam lingkaran

Beberapa istilah geometri mengenai lingkaran, yaitu:

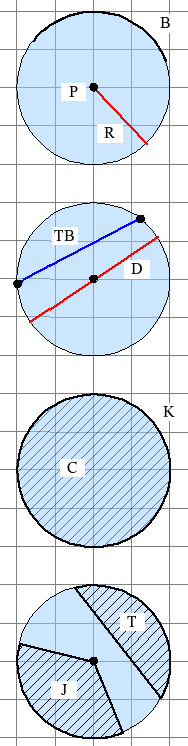
Istilah yang menunjukkan titik

- Titik pusat (P)
  merupakan titik tengah lingkaran, di mana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.

Istilah yang menunjukkan garisan

- Jari-jari (R)
  merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran.
- Tali busur (TB)
  merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
- Busur (B)
  merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran.
- Keliling lingkaran (K)
  merupakan busur terpanjang pada lingkaran.
- Diameter (D)
  merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas.
- Apotema
  merupakan garis terpendek antara tali busur dan pusat lingkaran.

Istilah yang menunjukkan luasan

- Juring (J)
  merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya.
- Tembereng (T)
  merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
- Cakram (C)
  merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.

Lambang Pi

Lambang π (baca: pi) dalam matematika menyatakan keliling lingkaran berdiameter 1 (yang sama dengan rasio keliling lingkaran sembarang terhadap diameternya).

Pada abad ke-3 SM, Archimedes menaksir nilai π kira-kira sama dengan 22/7. Lambang π sendiri baru diperkenalkan oleh matematikawan Inggris bernama William Jones pada tahun 1706.

Jawaban Kuis Matematika

Jawaban: 9

Karena Pi adalah 3.14159265359

Contoh Soal dan Jawaban Menggunakan Rumus Lingkaran

1. Jika diketahui sebuah lingkaran memiliki diameter 14 cm. Berapakah luas lingkaran tersebut?

Penyelesaian:

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

Diketahui:

d = 14 cm

karena d = 2 × r maka:

r = d/2
r = 14/2
r = 7 cm

Ditanyakan: Luas lingkaran?

Jawab:

Luas = p × r²
Luas = 22/7 × 7²
Luas = 154 cm²

Jadi, luas lingkaran tersebut adalah 154 cm².

2. Cindy adalah murid kelas 5 SD yang mempunyai tugas membuat sebuah gambar lingkaran denga dia meter 20cm. Tentukanlah luas lingkaran yang akan dibuat anak tersebut?

Penyelesaian:

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

Jawaban:

Diketahui yaitu:

d = 20 cm

maka:

r = 20/2 = 10 cm (karna d = 2 x r, maka r = d/2)

π = 3,14 atau 22/7 (ketetapan)

Yang ditanyakan:

Luas lingkaran: … ?

Penyelesaiannya, yaitu:

Gunakan rumus mencari luas lingkaran, yaitu:

Luas lingkaran = π x r²

Masukkanlah nilai yang diketahui ke dalam rumus:

L = π x r²

= 3,14 x 10²

= 3,14 x 100

= 314 cm²

Maka, luas lingkaran yang di gambar anak tersebut ialah sebesar 314 cm^2.

3. Jika diketahui keliling sebuah lingkaran adalah 88 cm dan nilai π adalah ²²⁄₇. Hitunglah berapakah luasnya?

Penyelesaian:

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

Jawaban:
Karena untuk menghitung luas lingkaran menggunakan rumus π x r², kita cari terlbih dahulu nilai r nya.
Keliling = 2.π.r
88 = 2.π.r
Balikan
r = 88
2.π
r = 88
2.(²²/7)
r = 88 x 7
44
r = 2 x 7
r = 14 cm

Setelah menemukan nilai jari-jari(r) selanjutnya kita hitung luasnya.
L = π x r²
L = ²²⁄₇ x 14²
L = ²²⁄₇ x 14 x 14
L = 616 cm²

4. Sebuah lingkaran mempunyai jari-jari sebesar 10 cm. Berapakah luas lingkaran tersebut?

Penyelesaian:

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

Diketahui:

r = 10 cm

Ditanyakan: Luas lingkaran?

Jawab:

Luas = p × r²
Luas = 3,14 × 100
Luas = 314 cm²

Jadi, luas lingkaran tersebut adalah 314 cm².

5. Diketahui sebuah lingkaran memiliki keliling sebesar 66 cm. Hitunglah berapa diameter lingkaran tersebut.

Penyelesaian:

Gunakan rumus lingkaran untuk mencari: Diameter lingkaran: 2.r

Diketahui:

Keliling = 66 cm

Ditanyakan: Diameter lingkaran?

Jawab:

Keliling = p × d

untuk mencari diameter, maka dibutuhkan rumusnya.

Rumus mencari diamter adalah d = keliling / p

d = 66 / (22/7)
d = (66 × 7) / 22
d = 21 cm

Jadi, diameter lingkaran tersebut adalah 21 cm.

6. Sebuah Ban sepeda BMX memiliki jari-jari 25 cm. Tentukanlah keliling lingkaran dari sebuah ban sepeda tersebut:

Penyelesaian:

Gunakan rumus lingkaran untuk mencari keliling lingkaran: Keliling = π x d

Jawab:

Diketahui:

r = 25 cm

π = 3,14 atau 22/7 (ketetapan)

Yang ditanyakan:

Keliling lingkaran: … ?

Penyelesaiannya, yaitu:

Gunakan rumus mencari keliling lingkaran:

Keliling lingkaran = π x 2 x r

Masukkanlah nilai yang sudah di ketahui kedalam rumus:

K = π x 2 x r

= 3,14 x 2 x 25

= 3,14 x 50

= 157 cm

Maka, keliling lingkaran tersebut sebesar 157 cm.

7. Jika diketahui sebuah lingkaran mempunyai jari-jari 14 cm dan π ( phi ) = 22/7, hitunglah luas lingkaran tersebut!

Penyelesaian:

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

Diketahui:

r = 14 cm
π ( phi ) = 22/7

L = π x r²
= 22/7 x 14²
= 22/7 x ( 14 x 14 )
= 22/7 x 196
= 4312/7
= 616
Jadi luas lingkaran tersebut adalah 616 cm²

8. Hitunglah keliling lingkaran dengan jari-jari 20 cm.

Penyelesaian:

Gunakan rumus lingkaran untuk mencari keliling lingkaran: Keliling = π x d

Diketahui:

r = 20 cm
p = 3,14

Ditanyakan: Keliling lingkaran?

Jawab:

Keliling = 2 × p × r
Keliling = 2 × 3,14 × 20
Keliling = 125,6 cm

Jadi, keliling lingkaran tersebut adalah 125,6 cm.>

9. Hitunglah keliling lingkaran dengan diameter 20 cm?

Penyelesaian:

Gunakan rumus lingkaran untuk mencari keliling lingkaran: Keliling = π x d

Diketahui:

d = 20 cm
p = 3,14

Ditanyakan: Keliling lingkaran?

Jawab:

Keliling = p × d
Keliling = 3,14 × 20
Keliling = 62,8 cm

Jadi, keliling lingkaran tersebut adalah 62,8 cm.

10. Jika diketahui sebuah lingkaran memiliki diameter 28 cm. Hitunglah luas lingkaran tersebut?

Penyelesaian:

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

Diketahui:

d = 28 cm
karena d = 2 × r maka:

r = d/2
r = 28/2
r = 14 cm
Ditanyakan: Luas lingkaran?

Jawab:

Luas = π × r²
Luas = 22/7 × 14²
Luas = 616 cm²
Jadi, luas lingkaran tersebut adalah 616 cm².

Angka Pi Yang Sebenarnya

3.1415926535897932384626433832795028841971693993751058209749445923078164062
86208998628034825342117067982148086513282306647093844609550582231725359408
12848111745028410270193852110555964462294895493038196442881097566593344612
84756482337867831652712019091456485669234603486104543266482133936072602491
41273724587006606315588174881520920962829254091715364367892590360

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: California Institute of Technology

Rumus-Rumus Lingkaran & Volume – Tes Matematika Lingkaran

Rumus Lingkaran

Luas lingkaran: Luas = π r2

Luas setengah lingkaran: L = 1/2 x π x r2

Diameter lingkaran: 2.r

Jari-jari lingkaran: r = K/2 phi

Keliling setengah lingkaran: K = π x r

Keliling lingkaran: Keliling = π x d

Rumus Volume

Tabel Rumus Volume

Test Matematika Lingkaran

3 1 4 1 5 ? 2 6 5 3 5 8 ? 7 ? 3

Angka berapa yang menggantikan tanda ?

Apakah Lingkaran?

Istilah-Istilah Dalam lingkaran

Istilah yang menunjukkan titik

Istilah yang menunjukkan garisan

Istilah yang menunjukkan luasan

Lambang Pi

Jawaban Kuis Matematika

Contoh Soal dan Jawaban Menggunakan Rumus Lingkaran

1. Jika diketahui sebuah lingkaran memiliki diameter 14 cm. Berapakah luas lingkaran tersebut?

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

2. Cindy adalah murid kelas 5 SD yang mempunyai tugas membuat sebuah gambar lingkaran denga dia meter 20cm. Tentukanlah luas lingkaran yang akan dibuat anak tersebut?

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

3. Jika diketahui keliling sebuah lingkaran adalah 88 cm dan nilai π adalah ²²⁄₇. Hitunglah berapakah luasnya?

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

4. Sebuah lingkaran mempunyai jari-jari sebesar 10 cm. Berapakah luas lingkaran tersebut?

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

5. Diketahui sebuah lingkaran memiliki keliling sebesar 66 cm. Hitunglah berapa diameter lingkaran tersebut.

Gunakan rumus lingkaran untuk mencari: Diameter lingkaran: 2.r

6. Sebuah Ban sepeda BMX memiliki jari-jari 25 cm. Tentukanlah keliling lingkaran dari sebuah ban sepeda tersebut:

Gunakan rumus lingkaran untuk mencari keliling lingkaran: Keliling = π x d

7. Jika diketahui sebuah lingkaran mempunyai jari-jari 14 cm dan π ( phi ) = 22/7, hitunglah luas lingkaran tersebut!

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

8. Hitunglah keliling lingkaran dengan jari-jari 20 cm.

Gunakan rumus lingkaran untuk mencari keliling lingkaran: Keliling = π x d

9. Hitunglah keliling lingkaran dengan diameter 20 cm?

Gunakan rumus lingkaran untuk mencari keliling lingkaran: Keliling = π x d

10. Jika diketahui sebuah lingkaran memiliki diameter 28 cm. Hitunglah luas lingkaran tersebut?

Gunakan rumus lingkaran untuk mencari luas lingkaran: Luas = π r2

Angka Pi Yang Sebenarnya

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan